8.1: Fuerzas Conservadoras

En el Capítulo 7, introdujimos el concepto de trabajo\(W\), hecho por una fuerza,\(\vec F(\vec r)\), que actúa sobre un objeto a medida que se mueve por un camino de una posición\(A\) a otra\(B\):

\[W=\int_{A}^{B} \vec F (\vec r)\cdot d\vec l\]

donde\(\vec F(\vec r)\) es un vector de fuerza que, en general, es diferente en diferentes posiciones en el espacio (\(\vec r\)). También podemos decir que\(\vec F\) depende de la posición escribiendo\(\vec F(\vec r)=\vec F(x,y,z)\), ya que el vector de posición,\(\vec r\), es simplemente el vector\(\vec r = x\hat x + y \hat y+ z\hat z\). Es decir,\(\vec F(\vec r)\) es solo una notación manual corta para\(\vec F(x,y,z)\), y\(d\vec l\) es un segmento (muy) pequeño a lo largo del camino particular sobre el cual se calcula la obra.

La integral anterior es, en general, difícil de evaluar, ya que depende de la trayectoria específica sobre la que se movió el objeto. En el Ejemplo 7.1.2 del Capítulo 7, calculamos el trabajo realizado por fricción sobre una caja que se deslizó por el piso a lo largo de dos caminos diferentes y efectivamente encontramos que la obra dependía del camino que se tomara. En el Ejemplo 7.1.3 del mismo capítulo, vimos que el trabajo realizado por la fuerza de la gravedad al mover una caja por dos caminos diferentes no dependía del camino elegido ¹.

Llamamos “fuerzas conservadoras” a aquellas fuerzas para las que el trabajo realizado sólo depende de las posiciones inicial y final y no del camino que se tome entre esas dos posiciones. Las fuerzas “no conservadoras” son aquellas para las que el trabajo realizado sí depende del camino que se tome. La fuerza de gravedad es un ejemplo de una fuerza conservadora, mientras que la fricción es un ejemplo de una fuerza no conservadora.

Esto significa que el trabajo realizado por una fuerza conservadora en un “camino cerrado” es cero; es decir, el trabajo realizado por una fuerza conservadora sobre un objeto es cero si el objeto se mueve a lo largo de un camino que lo devuelve a su posición inicial. En efecto, dado que el trabajo realizado por una fuerza conservadora sólo depende de la ubicación de las posiciones inicial y final, y no del camino tomado entre ellas, el trabajo tiene que ser cero si el objeto termina en el mismo lugar donde comenzó (un posible camino es para que el objeto no se mueva en absoluto).

Considerar el trabajo realizado por gravedad al elevar (desplazamiento\(\vec d_1\)) y bajar (desplazamiento\(\vec d_2=-\vec d_1\)) un objeto de regreso a su posición inicial a lo largo de una trayectoria vertical, como se representa en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un objeto que se ha movido hacia arriba y hacia abajo.

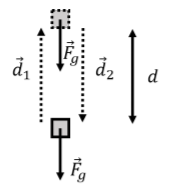
El trabajo total realizado por gravedad en este camino cerrado particular se muestra fácilmente como cero, ya que el trabajo puede dividirse en el trabajo negativo realizado a medida que el objeto se mueve hacia arriba (vector de desplazamiento\(\vec d_1\)) y el trabajo positivo realizado a medida que el objeto se mueve hacia abajo (vector de desplazamiento\(\vec d_2\)):

\[\begin{aligned} W^{tot} = \vec F_g \cdot \vec d_1 + \vec F_g \cdot \vec d_2 = -mgd + mgd = 0 \end{aligned}\]

Para escribir el camino integral de la fuerza sobre un trazado cerrado, introducimos una nueva notación para indicar que la posición inicial y final son las mismas:

\[\begin{aligned} \int_A^A \vec F(\vec r) \cdot d\vec l = \oint \vec F(\vec r) \cdot d\vec l\end{aligned}\]

La condición para que una fuerza sea conservadora es así:

\[\oint \vec F(\vec r) \cdot d\vec \ =0\]

ya que esto significa que el trabajo realizado sobre una trayectoria cerrada es cero. La condición para que esta integral sea cero se puede encontrar en el Teorema de Stokes:

\[\begin{aligned} \oint \vec F(\vec r) \cdot d\vec l = \int_S \left[\left(\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}\right)\hat x+ \left(\frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x}\right)\hat y + \left(\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}\right)\hat z \right]\cdot d\vec A\end{aligned}\]

donde la integral de la derecha se denomina “integral de superficie” sobre la superficie,\(S\), encerrada por la trayectoria cerrada sobre la que se calcula la obra. ¡No te preocupes, está mucho más allá del alcance de este texto entender en detalle esta integral o Teorema de Stokes! Sin embargo, es útil porque nos da las siguientes condiciones sobre los componentes de una fuerza para que esa fuerza sea conservadora (al exigir que los términos entre paréntesis sean cero):

\[\frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z}=0\]

\[\frac{\partial F_{x}}{\partial x}-\frac{\partial F_{z}}{\partial x}=0\]

\[\frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y}=0\]

En general:

1. Una fuerza puede ser conservadora si solo depende de la posición en el espacio, y no de la velocidad, el tiempo o cualquier otra cantidad.
2. Una fuerza es conservadora si es constante en magnitud y dirección.

Ejercicio\(\PageIndex{1}\)

Empujas una caja desde el punto\(A\) to point \(B\) along a horizontal surface. Is the force you exert a conservative force?

1. Sí
2. No
3. No hay suficiente información

Contestar

Ejemplo\(\PageIndex{1}\)

Es la fuerza de la gravedad sobre un objeto de masa\(m\), near the surface of the Earth, given by:

\[\begin{aligned} \vec F(x,y,z) =0\hat x + 0\hat y -mg \hat z\end{aligned}\]

¿conservadora? Tenga en cuenta que hemos definido el\(z\) axis to be vertical and positive upwards.

Solución:

Se espera que la fuerza sea conservadora ya que es constante en magnitud y dirección. Podemos verificar esto usando las condiciones de las Ecuaciones 8.1.3, 8.1.4 y 8.1.5:

\[\begin{aligned} \frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z} &= \frac{\partial}{\partial y}(-mg) - 0 &= 0\\ \frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x} &= 0 - \frac{\partial}{\partial x}(-mg) &= 0\\ \frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y} &= 0 - 0 &=0\end{aligned}\]

y la fuerza es efectivamente conservadora ya que las tres condiciones son cero.

Ejemplo\(\PageIndex{2}\)

¿Es conservadora la siguiente fuerza?

\[\begin{aligned} \vec F(x,y,z) = \frac{-k}{r^3}\vec r = \frac{-kx}{(x^2+y^2+z^2)^\frac{3}{2}}\hat x + \frac{-ky}{(x^2+y^2+z^2)^\frac{3}{2}}\hat y + \frac{-kz}{(x^2+y^2+z^2)^\frac{3}{2}}\hat z\end{aligned}\]

Solución:

Dado que la fuerza solo depende de la posición, podría ser conservadora, por lo que debemos verificar usando las condiciones de las Ecuaciones 8.1.3, 8.1.4 y 8.1.5:

\[\begin{aligned} \frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z} &= \frac{\partial }{\partial y}\left(\frac{-kz}{(x^2+y^2+z^2)^\frac{3}{2}}\right)-\frac{\partial}{\partial z}\left( \frac{-ky}{(x^2+y^2+z^2)^\frac{3}{2}}\right)\\ &=\frac{3kz(2y)}{2(x^2+y^2+z^2)^\frac{5}{2}}-\frac{3ky(2z)}{2(x^2+y^2+z^2)^\frac{5}{2}} = 0\\ \frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x} &= \frac{\partial}{\partial z}\left(\frac{-kx}{(x^2+y^2+z^2)^\frac{3}{2}}\right)-\frac{\partial}{\partial x}\left( \frac{-kz}{(x^2+y^2+z^2)^\frac{3}{2}}\right)\\ &=\frac{3kx(2z)}{2(x^2+y^2+z^2)^\frac{5}{2}}-\frac{3kz(2x)}{2(x^2+y^2+z^2)^\frac{5}{2}} = 0\\ \frac{\partial F_y}{\partial x}-\frac{\partial F_{x}}{\partial y} &= \frac{\partial}{\partial x}\left(\frac{-ky}{(x^2+y^2+z^2)^\frac{3}{2}}\right)-\frac{\partial}{\partial y}\left( \frac{-kx}{(x^2+y^2+z^2)^\frac{3}{2}}\right)\\ &=\frac{3ky(2x)}{2(x^2+y^2+z^2)^\frac{5}{2}}-\frac{3kx(2y)}{2(x^2+y^2+z^2)^\frac{5}{2}} = 0\end{aligned}\]

donde usamos la Regla de la Cadena para tomar los derivados. Dado que todas las condiciones son cero, la fuerza es conservadora. Como veremos, la fuerza aquí representada es similar matemáticamente tanto a la fuerza que Newton introdujo en su Teoría Universal de la Gravedad, como a la fuerza introducida por Coulomb como la fuerza eléctrica, que son ambas conservadoras.

Notas al pie

1. Al menos para esos dos caminos que probamos en el ejemplo.