8.2: Energía Potencial

En esta sección, introducimos el concepto de “energía potencial”. La energía potencial es una función escalar de posición que se puede definir para cualquier fuerza conservadora de manera que sea fácil calcular el trabajo realizado por esa fuerza sobre cualquier camino. Dado que el trabajo realizado por una fuerza conservadora al pasar de una posición\(A\) a otra\(B\) no depende del camino particular tomado, sino solo de los puntos finales, podemos escribir el trabajo realizado por una fuerza conservadora en términos de una “función energética potencial”, \(U(\vec r)\), que se puede evaluar en los puntos finales:

\[-W=-\int_{A}^{B} \vec F (\vec r )\cdot d\vec l =U(\vec r_{B} )-U(\vec r_{A})=\Delta U\]

donde hemos optado\(U(\vec r)\) por definir la función para que se relacione con lo negativo del trabajo realizado por razones que serán evidentes en el siguiente apartado. La figura\(\PageIndex{1}\) muestra un ejemplo de una trayectoria arbitraria entre dos puntos\(A\) y\(B\) en dos dimensiones para la cual se podría calcular el trabajo realizado por una fuerza conservadora utilizando una función de energía potencial.

Figura\(\PageIndex{1}\): Ilustración del cálculo del trabajo realizado por una función conservadora a lo largo de un camino arbitrario tomando la diferencia de energía potencial evaluada en los dos puntos finales,\(−W = U(\vec r_{B}) − U(\vec r_{A})\).

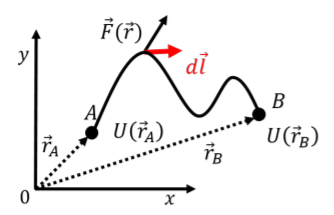
Una vez que conocemos la función para la energía potencial\(U(\vec r)\), podemos calcular el trabajo realizado por la fuerza asociada a lo largo de cualquier camino. Para determinar la función,\(U(\vec r)\), podemos calcular el trabajo que se realiza a lo largo de un camino sobre el cual la integral para el trabajo es fácil (generalmente, una línea recta).

Por ejemplo, cerca de la superficie de la Tierra, la fuerza de gravedad sobre un objeto de masa\(m\), viene dada por:

\[\begin{aligned} \vec F_g = -mg \hat z\end{aligned}\]

donde hemos definido el\(z\) eje para que sea vertical y positivo hacia arriba. Ya mostramos en el Ejemplo 8.1.1 que esta fuerza es conservadora y que así podemos definir una función energética potencial. Para ello, podemos calcular el trabajo realizado por la fuerza de la gravedad sobre una trayectoria vertical recta, de posición en posición\(A\)\(B\), como se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Trayectoria vertical para calcular la palabra realizada por gravedad.

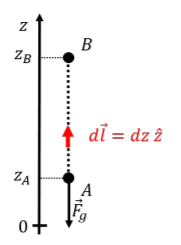
El trabajo realizado por gravedad de posición\(A\) a posición\(B\) es:

\[\begin{aligned} W &= \int_A^B \vec F(\vec r) \cdot d\vec l\\ &= \int_{z_A}^{z_B} ( -mg \hat z) \cdot (dz \hat z) \\ &= -mg \int_{z_A}^{z_B} dz\\ &= -mg(z_B-z_A) \end{aligned}\]

Por inspección, ahora podemos identificar la forma funcional para la función de energía potencial,\(U(\vec r)\).

Requerimos que:

\[\begin{aligned} -W &= U(\vec r_B) - U(\vec r_A) = U(z_B) - U(z_A)\end{aligned}\]

donde sustituimos el vector de posición,\(\vec r\), con la\(z\) coordenada, ya que se trata de una situación unidimensional. Por lo tanto:

\[\begin{aligned} -W=mg(z_B-z_A)&= U(z_B) - U(z_A)\\ \therefore U(z) &= mgz + C\end{aligned}\]

y hemos encontrado que, para la fuerza de gravedad cerca de la superficie de la Tierra, se puede definir una función de energía potencial (por inspección),\(U(z) = mgz +C\).

Es importante señalar que, dado que es sólo la diferencia de energía potencial lo que importa a la hora de calcular el trabajo realizado, la función de energía potencial puede tener una constante arbitraria,\(C\), sumada a la misma. Así, el valor de la función de energía potencial no tiene sentido, y solo las diferencias en la energía potencial son significativas y están relacionadas con el trabajo realizado en un objeto. En otras palabras, no importa dónde la energía potencial sea igual a cero, y al elegir\(C\), por lo tanto, podemos elegir una ubicación conveniente donde la energía potencial sea cero.

Ejercicio\(\PageIndex{1}\)

Cuando encontramos el trabajo realizado por gravedad, definimos positivo\(z\) to be upwards. If we instead chose positive \(z\) to be downwards, how would the potential energy function be defined?

1. La función energética potencial sería la misma,\(U(z)=mgz+C\).
2. La función energética potencial sería la misma pero negativa,\(U(z)=-mgz+C\)

Contestar

Ejercicio\(\PageIndex{2}\)

¿Puede un objeto tener una energía potencial negativa?

1. Sí
2. No

Contestar

Ejemplo\(\PageIndex{1}\)

Calcular el trabajo realizado por la fuerza de gravedad cuando una caja de masa,\(m\), is moved from the ground up onto a table that is a distance \(L\) away horizontally and \(H\) vertically, as illustrated in Figure \(\PageIndex{3}\). How much work must be done by a person moving the box?

Figura\(\PageIndex{3}\): Una caja movida del grupo hacia arriba sobre una mesa.

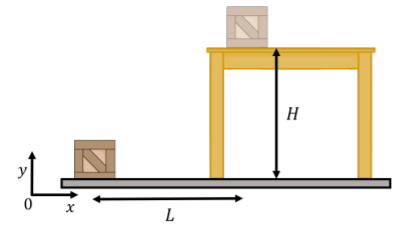
Solución:

Dado que la fuerza de gravedad es conservadora, podemos usar la función de energía potencial dada por:

\[\begin{aligned} U(z)=mgz+C\end{aligned}\]

para calcular el trabajo realizado por la fuerza de gravedad cuando se mueve la caja. El trabajo realizado por gravedad sólo dependerá del cambio de altura,\(H\), ya que la función de energía potencial sólo depende de la\(z\) coordenada de un objeto. Podemos elegir el origen de nuestro sistema de coordenadas para que sea el suelo y elegir la constante\(C=0\), de manera que la función de energía potencial en la posición inicial de la caja sea:

\[\begin{aligned} U(z_A=0) = mg(0)= 0\end{aligned}\]

La función de energía potencial cuando la caja está sobre la mesa, con\(z=H\), viene dada por:

\[\begin{aligned} U(z_B=H) = mgH\end{aligned}\]

El cambio en la energía potencial,\(\Delta U = U(z_B) - U(z_A)\) es igual a lo negativo del trabajo realizado por gravedad. El trabajo realizado por gravedad,\(W_g\), es así:

\[\begin{aligned} -W_g &= U(z_B) - U(z_A) = mgH - 0\\ \therefore W_g &= -mgH\end{aligned}\]

que es lo mismo que encontramos en el Ejemplo 7.1.3 del Capítulo 7. El trabajo realizado por gravedad es negativo, como encontramos anteriormente. Esto tiene sentido porque la gravedad tiene un componente opuesto a la dirección del movimiento.

El trabajo realizado por una persona,\(W_p\), para mover la caja se puede encontrar fácilmente considerando el trabajo de red realizado en la caja. Mientras la caja se mueve, solo la persona y la gravedad están ejerciendo fuerzas sobre la caja, por lo que esas son las únicas dos fuerzas que realizan el trabajo. Dado que la caja comienza y termina en reposo, el trabajo neto realizado en la caja debe ser cero (sin cambios en la energía cinética, recordar el Teorema de Trabajo-Energía):

\[\begin{aligned} W^{net} = 0 &= W_g + W_p\\ \therefore W_p &= -W_g = mgH\end{aligned}\]

Discusión:

Encontramos que la persona tuvo que hacer un trabajo positivo, lo cual tiene sentido, ya que tuvo que ejercer una fuerza con un componente en la dirección del movimiento (hacia arriba). También es interesante señalar que no importa si la persona ejerció una fuerza constante o si varió la fuerza que ejerció sobre la caja a medida que la movía: la cantidad de trabajo que realiza la persona se fija para que sea la negativa del trabajo realizado por gravedad.

Ejemplo\(\PageIndex{2}\)

La fuerza ejercida por un resorte que se extiende o comprime por una distancia,\(x\), is given by Hookes’ Law:

\[\begin{aligned} \vec F(x) = -k x\hat x\end{aligned}\]

donde se encuentra el\(x\) axis is defined to be co-linear with the spring and the origin is located at the rest position of the spring. Show that the force exerted by the spring onto an object is conservative and determine the corresponding potential energy function.

Solución:

Dado que la fuerza depende de la posición, podría ser conservadora, lo que podemos verificar con las condiciones de las Ecuaciones 8.1.3, 8.1.4, 8.1.5:

\[\begin{aligned} \frac{\partial F_{z}}{\partial y}-\frac{\partial F_{y}}{\partial z} &= 0 - 0 &= 0\\ \frac{\partial F_{x}}{\partial z}-\frac{\partial F_{z}}{\partial x} &= \frac{\partial}{\partial z}(-kx)) - 0&= 0\\ \frac{\partial F_{y}}{\partial x}-\frac{\partial F_{x}}{\partial y} &= 0 - \frac{\partial}{\partial y}(-kx)) &=0\end{aligned}\]

y la fuerza es, en efecto, conservadora. Para determinar la función de energía potencial, calculemos el trabajo realizado por el resorte de una posición\(x_A\) a\[\begin{aligned} W &=\int_A^B \vec F(\vec r) \cdot d\vec l\\ &=\int_{x_A}^{x_B} (-kx\hat x) \cdot dx \hat x\\ &=\int_{x_A}^{x_B} (-kx)dx=\left[-\frac{1}{2}kx^2 \right]_{x_A}^{x_B}\\ &=-\left( \frac{1}{2}kx_B^2-\frac{1}{2}kx_A^2 \right)\end{aligned}\] otra\(x_B\): De nuevo, comparando con:\[\begin{aligned} -W &= U(\vec r_B) - U(\vec r_A) = U(x_B) - U(x_A)\end{aligned}\] Podemos identificar la energía potencial para un resorte:\[\begin{aligned} U(x) = \frac{1}{2}kx^2 + C\end{aligned}\] donde, en general, la constante \(C\)puede tomar cualquier valor. Si elegimos\(C=0\), entonces la energía potencial es cero cuando la primavera está en reposo, aunque no es importante qué elección se hace. Obsérvese que en una dimensión, la función de energía potencial es la negativa de la anti-derivada de la función que da el\(x\) componente de la fuerza.

Ejercicio\(\PageIndex{3}\)

Una fuerza conservadora actúa sobre un objeto que inicialmente está en reposo. Ninguna otra fuerza actúa sobre el objeto. ¿El objeto se mueve de una manera que aumenta su energía potencial o disminuye su energía potencial?

1. Incrementos.
2. Disminuye.
3. Depende de la elección de\(C\) para la energía potencial correspondiente.

Contestar

Recuperar la fuerza de la energía potencial

Dada una función de energía potencial (escalar)\(U(\vec r)\), es posible determinar la fuerza (vector) que está asociada a ella. Tomemos, por ejemplo, la energía potencial de un resorte (Ejemplo 8.2.2):\[\begin{aligned} U(x) = \frac{1}{2}kx^2 + C\end{aligned}\] Como recuerda del Ejemplo 8.2.2, para encontrar esta función (en una dimensión), tomamos el\(x\) componente de la fuerza del resorte y (efectivamente) encontramos lo negativo de su anti-derivado , que definimos como la función de energía potencial:\[\begin{aligned} F(x) &= -kx\\ U(x) &= -\int F(x) dx = \int (kx) dx = \frac{1}{2}kx^2+C\\ \therefore F(x) &= -\frac{d}{dx}U(x)\end{aligned}\] Así, la fuerza se puede obtener de lo negativo de la función de energía potencial, tomando su derivada con respecto a la posición.

En tres dimensiones, la situación es similar, aunque la función de energía potencial (y los componentes del vector de fuerza) generalmente dependerán de las tres coordenadas de posición,\(x\),\(y\), y\(z\). En tres dimensiones, los tres componentes del vector de fuerza se dan tomando el gradiente del negativo de la función de energía potencial ¹:

\(\vec F(\vec r )=-\vec\nabla U(\vec r)=-\vec\nabla U(x,y,z)\)

\[\therefore F_{x}(x,y,z) =-\frac{\partial}{\partial x} U(x,y,z)\]

\[\therefore F_{y}(x,y,z) =-\frac{\partial}{\partial y} U(x,y,z)\]

\[\therefore F_{z}(x,y,z) =-\frac{\partial}{\partial z} U(x,y,z)\]

Notas al pie

1. Como recordarás del Apéndice B, el gradiente es un vector que apunta hacia la dirección del aumento máximo en una función multi-variable.