8.3: Energía Mecánica y Conservación de Energía

Recordemos el Teorema Trabajo-Energía, que relaciona el trabajo neto realizado en un objeto con su cambio en la energía cinética, a lo largo de un camino de punto\(A\) a punto\(B\):\[\begin{aligned} W^{net}=\Delta K = K_B - K_A\end{aligned}\] dónde\(K_A\) está la energía cinética inicial del objeto y\(K_B\) es su final energía cinética. Generalmente, el trabajo neto realizado es la suma del trabajo realizado por las fuerzas conservadoras,\(W^C\), y el trabajo realizado por ninguna fuerza conservadora,\(W^{NC}\):\[\begin{aligned} W^{net}=W^C+W^{NC}\end{aligned}\] El trabajo realizado por las fuerzas conservadoras puede expresarse en términos de cambios en las funciones energéticas potenciales. Por ejemplo, supongamos que dos fuerzas conservadoras,\(\vec F_1\) y\(\vec F_2\), se ejercen sobre el objeto. El trabajo que realizan esas dos fuerzas viene dado por:\[\begin{aligned} W_1 &= -\Delta U_1\\ W_2 &= -\Delta U_2\end{aligned}\] dónde\(U_1\) y\(U_2\) son los cambios en la energía potencial asociados a las fuerzas\(\vec F_1\) y\(\vec F_2\), respectivamente. Podemos reorganizar el Teorema de Trabajo-Energía de la siguiente manera ¹:

\[\begin{aligned} W^{net}=W^C+W^{NC}=-\Delta U_1 - \Delta U_2 +W^{NC} &= \Delta K\\ \therefore W^{NC} = \Delta U_1 + \Delta U_2 + \Delta K\end{aligned}\]Es decir, el trabajo que realizan las fuerzas no conservadoras es igual a la suma de los cambios en las energías potenciales y cinéticas. En general, podemos utilizar\(\Delta U\) para representar el cambio en la energía potencial total del objeto. La energía potencial total es la suma de las energías potenciales asociadas a cada una de las fuerzas conservadoras que actúan sobre el objeto (\(\Delta U = \Delta U_1 + \Delta U_2\)arriba). Por lo tanto, la expresión anterior se puede escribir de una forma más general:

\[W^{NC}=\Delta U+\Delta K\]

En particular, tenga en cuenta que si no hay fuerzas no conservadoras haciendo trabajo sobre el objeto:

\[\Delta K+\Delta U=0\text{ if no non-conservative forces}\]

\(-\Delta U=\Delta K\)

Es decir, la suma de los cambios en las energías potenciales y cinéticas del objeto es siempre cero. Esto significa que si la energía potencial del objeto aumenta, entonces la energía cinética del objeto debe disminuir en la misma cantidad.

Podemos introducir la “energía mecánica”\(E\), de un objeto como la suma de las energías potenciales y cinéticas del objeto:

\[E=U+K\]

Si el objeto comenzó en posición\(A\), con energía potencial\(U_A\) y energía cinética\(K_A\), y terminó en posición\(B\) con energía potencial\(U_B\) y energía cinética\(K_B\), entonces podemos escribir el energía mecánica en ambas posiciones y su cambio\(\Delta E\), como:

\[\begin{aligned} E_A &= U_A + K_A\\ E_B &= U_B + K_B\\ \Delta E &= E_B - E_A \\ &= U_B + K_B - U_A - K_A\\ \therefore \Delta E &= \Delta U + \Delta K\end{aligned}\]

Así, el cambio en la energía mecánica del objeto es igual al trabajo realizado por fuerzas no conservadoras:

\[\begin{aligned} W^{NC} = \Delta U + \Delta K = \Delta E\end{aligned}\]

y si no hay trabajo realizado por fuerzas no conservadoras sobre el objeto, entonces la energía mecánica del objeto no cambia:

\[\begin{aligned} \Delta E &= 0\quad\text{if no non-conservative forces}\\ \therefore E &= \text{constant}\end{aligned}\]

Esto es lo que generalmente llamamos la “conservación de la energía mecánica”. Si no hay fuerzas no conservadoras haciendo trabajo sobre un objeto, su energía mecánica se conserva (es decir, constante).

La introducción de la energía mecánica nos da una manera completamente diferente de pensar sobre la mecánica. Ahora podemos pensar que un objeto tiene “energía” (potencial y/o cinética), y podemos pensar que las fuerzas cambian la energía del objeto.

Ejercicio\(\PageIndex{1}\)

¿Es significativo el valor de la energía mecánica de un objeto o solo la diferencia en la energía mecánica lo que es significativo?

1. Sí, el valor de la energía mecánica es significativo. En cualquier momento dado, un objeto tendrá una cantidad cuantificable de energía mecánica.
2. No, el valor no es significativo porque el valor de la energía potencial es arbitrario. Solo las diferencias en la energía mecánica son significativas.
3. No, el valor no es significativo porque tanto las energías potenciales como las energías cinéticas son arbitrarias. Sus valores cambiarán dependiendo de donde se establezca que la energía sea cero.
4. Depende de qué fuerzas conservadoras actúen sobre el objeto (y por lo tanto qué “tipo” de energía potencial tiene el objeto).

Contestar

También podemos pensar en el trabajo realizado por fuerzas no conservadoras como un tipo de cambio en la energía. Por ejemplo, el trabajo realizado por fricción puede pensarse como un cambio en la energía térmica (¡siente la quemadura mientras te frotas la mano vigorosamente sobre una mesa!). Si podemos modelar el trabajo realizado por fuerzas no conservadoras como un tipo de “otra” energía\(-W^{NC}=\Delta E^{other}\), entonces podemos afirmar eso:\[\begin{aligned} \Delta E^{other} + \Delta U + \Delta K =0\end{aligned}\] que es lo que solemos denominar “conservación de energía”. Es decir, la energía total en un sistema, incluyendo cinética, potencial y cualquier otra forma (ej. térmica, eléctrica, etc.) es constante a menos que algún agente externo esté actuando sobre el sistema.

Siempre podemos incluir ese agente externo en el sistema para que la energía total del sistema sea constante. El sistema más grande que podemos tener es el propio Universo. Así, la energía total en el Universo es constante y sólo puede transformarse de un tipo a otro, pero nunca se puede añadir ni quitar energía del Universo.

Pensamientos de Olivia

Aquí hay un ejemplo que puede ayudarte a entender el concepto de agentes externos y conservación de energía. Digamos que tenemos una masa que cuelga de un resorte, para que la masa oscile hacia arriba y hacia abajo como un yoyo. Si definimos nuestro sistema para incluir el resorte, la masa y la gravedad, la energía se conservará (la energía se transforma de energía potencial a energía cinética y de nuevo).

Ahora bien, ¿y si alguien está sosteniendo el final de la primavera y empiezan a caminar para que todo el sistema se acelere? La energía no se conserva porque el sistema está ganando energía cinética, aparentemente de la nada. El sistema está siendo actuado por un agente externo (la persona). Si expandimos nuestro sistema para que incluya el resorte, la masa, la gravedad y la persona, la energía se conserva. En lugar de la energía cinética “saliendo de la nada”, podemos ver que en realidad viene de la persona que convierte la energía química en su cuerpo para mover sus músculos.

Figura\(\PageIndex{1}\): Una persona acelera una masa y primavera caminando. Si el sistema no incluye a la persona, la energía no se conserva. Si incluye a la persona, se conserva la energía.

Pero, ¿y si hay un agente externo actuando sobre nuestro nuevo sistema? Podemos seguir “alejando” para incluir cada vez más fuentes externas en la definición de nuestro sistema. Si seguías alejando el zoom, eventualmente llegarías al punto en el que todo el Universo estaba incluido en tu sistema. En este punto, ya no se puede alejar más. Esto quiere decir que, si el Universo es su sistema, la energía debe conservarse siempre porque no puede haber ningún agente externo que actúe sobre el sistema.

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{2}\): Un bloque se lanza a lo largo de una superficie sin fricción comprimiendo un resorte por una distancia\(D\). El panel superior muestra el resorte cuando está en reposo, y el panel inferior muestra el resorte comprimido por una distancia\(D\) justo antes de liberar el bloque.

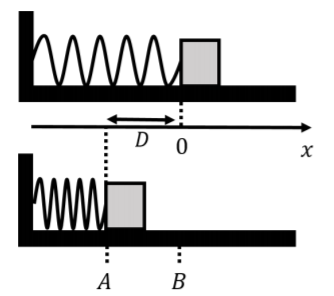
Un bloque de masa\(m\) puede deslizarse a lo largo de una superficie horizontal sin fricción. Un resorte horizontal, con constante de resorte\(k\), está unido a una pared en un extremo, mientras que el otro extremo puede moverse, como se muestra en la Figura 8.3.2. Se define un sistema de coordenadas de tal manera que el\(x\) eje es horizontal y el extremo libre del resorte está en\(x=0\) cuando el resorte está en reposo. El bloque se empuja contra el resorte para que el resorte se comprima por una distancia\(D\). Luego se libera el bloque. ¿Qué velocidad tendrá el bloque cuando salga del muelle?

Solución:

Este es nuevamente el mismo ejemplo que vimos en los Capítulos 6 y 7. Aquí mostraremos que se resuelve muy fácilmente utilizando la conservación de energía. Las fuerzas que actúan sobre el bloque son:

1. Peso, que no funciona ya que es perpendicular al desplazamiento del bloque.
2. La fuerza normal, que no funciona ya que es perpendicular al desplazamiento del bloque.
3. La fuerza del resorte, que es conservadora y puede modelarse con una energía potencial\(U(x)=\frac{1}{2}kx^2\), donde\(x\) está la posición del extremo del resorte.

El bloque comienza en reposo en la posición\(A\) (\(x=-D\)), donde el resorte se comprime por una distancia\(D\), y deja el resorte en la posición\(B\) (\(x=0\)), donde el resorte está en su posición de reposo.

En la posición\(A\), la energía cinética del bloque es\(K_A=0\) ya que el bloque está en reposo, y la energía potencial de la fuerza de resorte del bloque es\(U_A=\frac{1}{2}kD^2\). La energía mecánica del bloque en la posición\(A\) es así:\[\begin{aligned} K_A&=0\\ U_A&=\frac{1}{2}kD^2\\ \therefore E_A &= U_A + K_A = \frac{1}{2}kD^2\end{aligned}\] En la posición\(B\), la energía potencial de resorte del bloque es cero (ya que el resorte está en reposo), y toda la energía es cinética:\[\begin{aligned} K_B&=\frac{1}{2}mv_B^2\\ U_B&=0\\ \therefore E_B &= U_B+K_B=\frac{1}{2}mv_B^2\end{aligned}\] Dado que no hay fuerzas no conservadoras haciendo trabajo en el bloque, las energías mecánicas en\(A\) y\(B\) son las mismas:\[\begin{aligned} W^{NC}&=\Delta E=E_B-E_A= 0\\ \therefore E_B&=E_A\\ \frac{1}{2}mv_B^2&= \frac{1}{2}kD^2\\ v_B &= \sqrt{\frac{kD^2}{m}}\end{aligned}\] como encontramos anteriormente.

Ejemplo\(\PageIndex{2}\)

Figura\(\PageIndex{3}\): Un bloque se desliza por una pendiente antes de deslizarse sobre una superficie plana y detenerse.

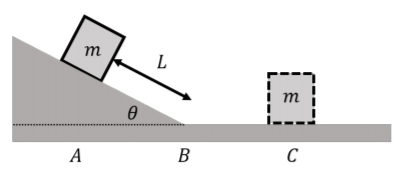
Un bloque de masa\(m\) is placed at rest on an incline that makes an angle \(\theta\) with respect to the horizontal, as shown in Figure \(\PageIndex{3}\). The block is nudged slightly so that the force of static friction is overcome and the block starts to accelerate down the incline. At the bottom of the incline, the block slides on a horizontal surface. The coefficient of kinetic friction between the block and the incline is \(\mu_{k1}\), and the coefficient of kinetic friction between the block and horizontal surface is \(\mu_{k2}\). If one assumes that the block started at rest a distance \(L\) from the bottom of the incline, how far along the horizontal surface will the block slide before stopping?

Solución

Este es el mismo problema que resolvimos en el Ejemplo 6.2.1. En ese caso, resolvimos la aceleración del bloque usando la Segunda Ley de Newton y luego usamos la cinemática para encontrar hasta dónde llegó el bloque. Podemos resolver este problema de una manera mucho más fácil utilizando la conservación de energía.

Todavía es una buena idea pensar qué fuerzas se aplican sobre el objeto para determinar si hay fuerzas no conservadoras haciendo trabajo. En este caso, las fuerzas sobre el bloque son:

1. La fuerza normal, que no funciona, ya que siempre es perpendicular al movimiento.
2. Peso, que sí funciona cuando cambia la altura del objeto, que podemos modelar con una función energética potencial.
3. La fricción, que es una fuerza no conservadora, cuyo trabajo debemos determinar.

Dividamos el movimiento en dos segmentos: (1) un segmento a lo largo de la inclinación (posiciones\(A\) a\(B\) en la Figura\(\PageIndex{3}\)), donde la energía potencial gravitacional cambia, y (2), el segmento horizontal de posiciones\(B\) a posición\(C\) en la figura. Entonces podemos aplicar la conservación de energía para cada segmento.

Comenzando con el primer segmento, podemos elegir que la energía potencial gravitacional sea cero cuando el bloque está en la parte inferior de la pendiente. El bloque comienza a una altura\(h=L\sin\theta\) por encima de la parte inferior de la inclinación. La energía potencial gravitacional para el inicio y el final del primer segmento son así:

\[\begin{aligned} U_A &= mgL\sin\theta\\ U_B &= 0\end{aligned}\]

Dado que el bloque comienza en reposo, su energía cinética es cero en la posición\(A\), y si la velocidad de la caja está\(v_B\) en posición\(B\), podemos escribir su energía cinética en ambas posiciones como:

\[\begin{aligned} K_A &=0\\ K_B &= \frac{1}{2}mv_B^2\end{aligned}\]La energía mecánica del objeto en las posiciones\(A\) y\(B\) es así:\[\begin{aligned} E_A &= U_A+K_A = mgL\sin\theta\\ E_B &= U_B+K_B = \frac{1}{2}mv_B^2\\ \Delta E &= E_B - E_A = \frac{1}{2}mv_B^2 - mgL\sin\theta\end{aligned}\]

Finalmente, dado que tenemos una fuerza no conservadora, la fuerza de fricción cinética, actuando sobre el primer segmento, necesitamos calcular el trabajo realizado por esa fuerza. Encontramos en el Ejemplo 6.2.1 que la fuerza de fricción tuvo magnitud\(f_k=\mu_{k1}N=\mu_{k1}mg\cos\theta\). Dado que la fuerza de fricción es antiparalela al vector de desplazamiento, que apunta hacia abajo en la pendiente y tiene longitud\(L\), el trabajo realizado por fricción es:\[\begin{aligned} W^{NC}=W_f = -f_kL=-\mu_{k1}mg\cos\theta L\end{aligned}\] Aplicando la conservación de energía a lo largo del primer segmento, tenemos:

\[\begin{aligned} W^{NC} &= \Delta E\\ -\mu_{k1}mg\cos\theta L &= \frac{1}{2}mv_B^2 - mgL\sin\theta\\ \therefore \frac{1}{2}mv_B^2 &= mgL\sin\theta-\mu_{k1}mg\cos\theta L \end{aligned}\]

Obsérvese que la ecuación anterior, en palabras, podría leerse como, “el cambio en la energía cinética (\(\frac{1}{2}mv_B^2\)) es igual al cambio negativo en la energía potencial (\(mgL\sin\theta\)) menos el trabajo realizado por fricción (\(\mu_{k1}mg\cos\theta L\))”. Es decir, el bloque tenía energía potencial, la cual se convirtió en energía cinética y calor (el trabajo realizado por fricción puede considerarse como energía térmica).

Ahora procedemos de manera análoga para el segundo segmento, de posición\(B\) en posición\(C\). La única fuerza que puede hacer trabajo a lo largo de este segmento (de longitud\(x\)) es la fuerza de fricción cinética, ya que tanto el peso como la fuerza normal son perpendiculares al desplazamiento. No hay fuerzas conservadoras haciendo trabajo, por lo que no hay cambio en la energía potencial. La energía cinética inicial es\(K_B\) (desde arriba), y la energía cinética final,\(K_C\), es cero. El cambio en la energía mecánica es así:

\[\begin{aligned} \Delta E &= E_C - E_B = K_C - K_B = -K_B\\ &=-\frac{1}{2}mv_B^2\\ &=- mgL\sin\theta+\mu_{k1}mg\cos\theta L \end{aligned}\]

donde, en la última línea, se utilizó el resultado del primer segmento. El trabajo realizado por la fuerza de fricción a lo largo del segmento horizontal de longitud (indeterminada)\(x\) es:

\[\begin{aligned} W^{NC}=W_f = -f_kx = -\mu_{k2} N x=-\mu_{k2} mg x\end{aligned}\]

Finalmente, podemos encontrar\(x\) fijando el trabajo realizado por fuerzas no conservadoras igual al cambio en la energía mecánica:

\[\begin{aligned} W^{NC} &= \Delta E\\ -\mu_{k2} mg x &=- mgL\sin\theta+\mu_{k1}mg\cos\theta L \\ \therefore x&= L\frac{1}{\mu_{k2}}\left(\sin\theta - \mu_{k1}\cos\theta\right)\end{aligned}\]

que es el mismo resultado que obtuvimos en el Ejemplo 6.2.1.

Discusión

Al utilizar la conservación de energía, pudimos modelar el movimiento del bloque por la pendiente de una manera mucho más fácil que lo que se hizo en el Ejemplo 6.2.1. Además, aunque modelamos la fricción como una fuerza no conservadora que trabaja, obtuvimos una idea de que esto podría considerarse como una pérdida de energía. En términos de energía, diríamos que el bloque inicialmente tenía energía potencial gravitacional, que luego se convirtió en energía cinética así como energía térmica (en el calor generado por la fricción).

Notas al pie

1. Es por ello que definimos la energía potencial como negativa de la obra; ¡se convierte en un término positivo cuando la movemos al mismo lado de la ecuación que la energía cinética!