8.4: Diagramas y equilibrios energéticos

Podemos escribir la energía mecánica de un objeto como:\[\begin{aligned} E = K + U\end{aligned}\] que será una constante si no hay fuerzas no conservadoras haciendo trabajo sobre el objeto. Esto significa que si la energía potencial del objeto aumenta, entonces su energía cinética debe disminuir en la misma cantidad, y viceversa.

Considera un bloque que pueda deslizarse sobre una superficie horizontal sin fricción y que esté unido a un muelle, como se muestra en la Figura\(\PageIndex{1}\) (lado izquierdo), donde\(x=0\) se elige como la posición correspondiente a la longitud de descanso del muelle. Si empuja el bloque para comprimir el resorte una distancia\(D\) y luego lo suelta, el bloque inicialmente acelerará debido a la fuerza del resorte en la\(x\) dirección positiva hasta que el bloque llegue a la posición de reposo del resorte (\(x=0\)en el diagrama). Cuando pase ese punto, el resorte ejercerá una fuerza en sentido contrario. El bloque continuará en la misma dirección y desacelerará hasta que se detenga y dé la vuelta. Luego acelerará nuevamente hacia la posición de reposo del resorte, y luego desacelerará una vez que el resorte comience a comprimirse nuevamente, hasta que el bloque se detenga y el movimiento se repita. Decimos que el bloque “oscila” de un lado a otro sobre la posición de descanso del resorte.

Podemos describir el movimiento del bloque en términos de su energía mecánica total,\(E\). Su energía potencial viene dada por:\[\begin{aligned} U(x)=\frac{1}{2}kx^2\end{aligned}\] A la derecha de la Figura\(\PageIndex{1}\) se encuentra un “Diagrama de Energía” para el bloque, que nos permite examinar cómo se divide la energía total\(E\),, del bloque entre energía cinética y potencial dependiendo de la posición del bloque. El eje vertical corresponde a la energía y el eje horizontal corresponde a la posición del bloque.

La energía mecánica total,\(E=\SI{25}{J}\), se muestra por la línea roja horizontal. También se ilustran la función de energía potencial (\(U(x)\)en azul), y la energía cinética, (\(K=E-U(x)\), en negro punteado).

Figura\(\PageIndex{1}\): Izquierda: El bloque oscila alrededor de la posición de reposo del resorte, entre\(x = −D\) y\(x = D\). Derecha: El diagrama de energía para el bloque. Este diagrama es para un resorte con constante de resorte\(k = 1 \text{N/m}\).

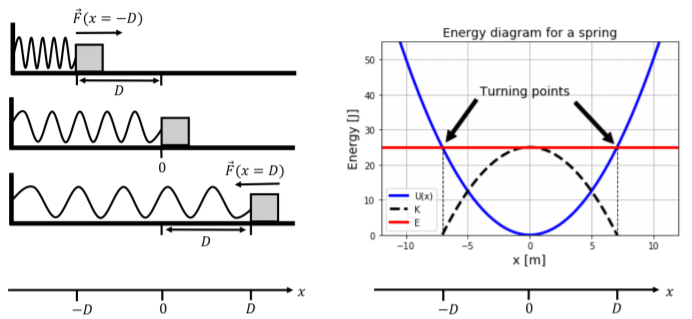
El diagrama de energía nos permite describir el movimiento del objeto unido al resorte en términos de energía. Algunas cosas a tener en cuenta:

1. At\(x=\pm D\), la energía potencial es igual a\(E\), por lo que la energía cinética es cero. El bloque se encuentra así instantáneamente en reposo en esas posiciones.
2. At\(x=0\), la energía potencial es cero, y la energía cinética es máxima. Esto corresponde a donde el bloque tiene la velocidad más alta.
3. La energía cinética del bloque nunca puede ser negativa ¹, así, el bloque no puede ubicarse fuera del rango\([-D,+D]\), y diríamos que el movimiento del bloque está “ligado”. Los puntos entre los que se encuadra el movimiento se denominan “puntos de inflexión”.

Un análisis del diagrama de energía nos dice que el bloque está ligado entre los dos puntos de inflexión, que a su vez son equidistantes del origen. Cuando inicialmente comprimimos el resorte, estamos “dando” al bloque “energía potencial de resorte”. A medida que el bloque comienza a moverse, la energía potencial del bloque se convierte en energía cinética a medida que se acelera y luego vuelve a energía potencial a medida que desacelera.

Ejercicio\(\PageIndex{1}\)

Calcular las posiciones de los puntos de inflexión para la situación mostrada en la Figura\(\PageIndex{1}\). La energía total es\(25\text{ J}\) y la constante de resorte es\(k=\SI{1}{N/m}\).

Contestar

\(7.1\text{ m}\)

Al mirar solo la función de energía potencial, sin saber que está relacionada con un resorte, podemos llegar a las mismas conclusiones; es decir, que el movimiento está ligado siempre y cuando la energía mecánica total no sea infinita. Llamamos al punto\(x=0\) un “equilibrio estable”, porque es un mínimo local de la función energética potencial. Si el objeto es desplazado del punto de equilibrio, querrá retroceder hacia ese punto. Esto también se puede entender en términos de la fuerza asociada a la función de energía potencial:

\[\begin{aligned} F = -\frac{d}{dx}U(x)\end{aligned}\]

El mínimo local ocurre donde la derivada de la función potencial es igual a cero. Así, el punto de equilibrio viene dado por la condición de que la fuerza asociada al potencial sea cero (\(x=0\)en el caso de la energía potencial de un resorte). El equilibrio es un equilibrio estable porque la fuerza asociada con la función de energía potencial (\(F(x)=-kx\)para el resorte) apunta hacia el punto de equilibrio.

La función de energía potencial para un objeto con energía mecánica total,\(E\), puede pensarse como una pequeña “montaña rusa”, en la que se coloca una canica y se ve “rodar hacia abajo” la función de energía potencial. Se puede pensar en colocar una canica donde\(U(x)=E\) y soltarla. El mármol entonces rodaría por la función de energía potencial, así como un mármol real rodaría por una pendiente real, imitando el movimiento del objeto a lo largo del\(x\) eje. Esto se ilustra en la Figura\(\PageIndex{2}\) que muestra una función arbitraria de energía potencial y un mármol que se coloca en una ubicación donde la energía potencial es igual a\(E\).

Figura\(\PageIndex{2}\): Función arbitraria de energía potencial e ilustración de visualizar un mármol rodando hacia abajo de la función colocando el mármol sobre la función de energía potencial en un punto donde\(U(x) = E\).

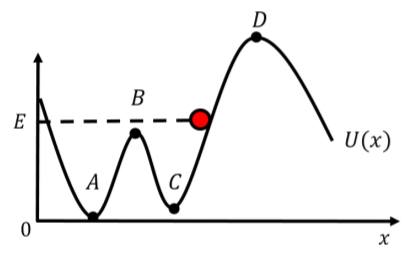
El movimiento del mármol se unirá entre los dos puntos donde la función de energía potencial es igual a\(E\). Cuando el mármol se coloca como se muestra, rodará hacia la izquierda, igual que si se tratara de un mármol real sobre una pista. Dado que la energía potencial está aumentando en función de\(x\) en el punto donde colocamos el mármol, la fuerza está en la\(x\) dirección negativa (recuerde, la fuerza es la negativa de la derivada de la función de energía potencial). Con la energía dada, el mármol nunca sería capaz de hacerlo a punto\(D\), ya que no tiene suficiente energía para “subir la colina”. Rodaría hacia abajo, a través de punto\(C\), de arriba a punto\(B\), de abajo a punto\(A\), para luego dar la vuelta a donde\(U(x)=E\) y regresar a donde empezó.

Las ubicaciones\(A\) y\(C\) en el diagrama son equilibrios estables, ya que si se coloca una canica en una de esas ubicaciones y se empuja ligeramente, volverá al punto de equilibrio (u oscilará alrededor de ese punto). Los puntos\(B\) y\(D\) son “equilibrios inestables”, porque si el mármol se coloca ahí y se le da un empujón, no volverá inmediatamente a esos puntos. Obsérvese que si el mármol fuera colocado en punto\(D\) y empujado hacia la derecha, el movimiento del mármol quedaría desatado a la derecha, y seguiría yendo en esa dirección.

Ahora, digamos que la energía potencial de un objeto es descrita por la función en la Figura\(\PageIndex{2}\), y el objeto tiene energía total\(E\). El movimiento del objeto a lo largo del\(x\) eje será exactamente el mismo que la proyección del movimiento del mármol sobre el\(x\) eje.

Ejercicio\(\PageIndex{2}\)

Una fuerza,\(F(x)\), acts on an object. The potential energy function, \(U(x)\), associated with the force is given by \(U(x)=a(x-6)^2(x-1)(x-3)+\SI{20}{J}\), where \(a\) is a positive constant. \(U(x)\) is plotted in Figure \(\PageIndex{3}\). Use the “marble” method to determine the direction of the force at \(x=5\). Confirm your answer by finding the value of the force , \(F(x)\), at \(x=5\).

Figura\(\PageIndex{3}\): Una función energética potencial\(U(x)\). El\(x\) eje -representa la\(x\) posición y el\(y\) -eje representa la energía.

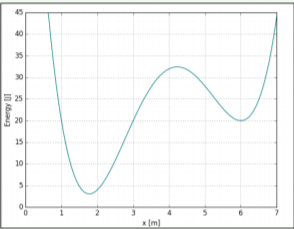
1. \(F(x=5)=-10a\)
2. \(F(x=5)=10a\)
3. \(F(x=5)=20a\)
4. \(F(x=5)=-20a\)

Contestar

Notas al pie

1. Recuerda, la energía cinética viene dada por\(K = \frac{1}{2}mv^{2}\). Dado que ni la masa ni el valor de\(v^{2}\) pueden ser negativos, la energía cinética de un objeto nunca puede ser negativa.