9.3: Energía potencial gravitacional

Considera un gran cuerpo esférico de masa\(M\) con un sistema de coordenadas cuyo origen coincide con el centro del cuerpo esférico (por ejemplo, el cuerpo grande podría ser la Tierra). La fuerza,\(\vec F(\vec r)\) sobre un cuerpo de masa\(m\) (por ejemplo, un satélite), ubicada en una posición\(\vec r\) viene dada entonces por:\[\begin{aligned} \vec F(\vec r) = - G\frac{Mm}{r^2}\hat r=- G\frac{Mm}{r^3}\vec r\end{aligned}\] donde en la segunda igualdad, usamos el hecho de que el vector unitario en la dirección de\(\vec r\) es simplemente el vector \(\vec r\)dividido por su magnitud. Podemos escribir la fuerza en coordenadas cartesianas:

\[\begin{aligned} \vec r &= x\hat x + y \hat y + z\hat z\\ r &= \sqrt{x^2+y^2+z^2} =(x^2+y^2+z^2)^\frac{1}{2} \\ \therefore \vec F(x,y,z) &= - G\frac{Mm}{(x^2+y^2+z^2)^\frac{3}{2} }(x\hat x + y \hat y + z\hat z)\end{aligned}\]

Matemáticamente, esto equivale a la fuerza que consideramos en el Ejemplo 8.1.2 del Capítulo 8, que demostramos que era una fuerza conservadora. La fuerza de gravedad en la teoría de Newton es así una fuerza conservadora, para lo cual podemos determinar una función energética potencial.

Para determinar la función de energía potencial gravitacional para la masa\(m\) en presencia de una masa\(M\), calculamos el trabajo realizado por la fuerza de gravedad sobre la masa\(m\) sobre un camino donde la integral para el trabajo será “fácil” de evaluar, es decir, una línea recta. La figura\(\PageIndex{1}\) muestra tal trayectoria en la dirección radial,\(r\), sobre la cual será fácil calcular el trabajo realizado por la fuerza de gravedad a partir de la masa\(M\) cuando la masa\(m\) se mueve de una distancia\(r_A\) a una distancia \(r_B\)desde el centro de masa\(M\).

Figura\(\PageIndex{1}\): Calcular el trabajo realizado sobre una masa m por la fuerza de gravedad ejercida por la masa\(M\) cuando la masa\(m\) se mueve de una distancia\(r_{A}\) a una\(r_{B}\) distancia del centro de masa\(M\).

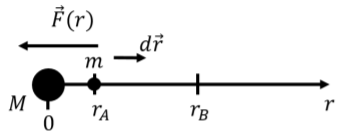
El trabajo realizado por la fuerza de gravedad al pasar de\(r_A\) a\(r_B\) viene dado por:\[\begin{aligned} W &= \int_{r_A}^{r_B}\vec F(r) \cdot d\vec r = \int_{r_A}^{r_B} \left(- G\frac{Mm}{r^2}\hat r \right)\cdot d\vec r =\int_{r_A}^{r_B} - G\frac{Mm}{r^2}dr\\ &=\left[G\frac{Mm}{r} \right]_{r_A}^{r_B} =G\frac{Mm}{r_B} - G\frac{Mm}{r_A}\end{aligned}\] La diferencia de energía potencial al pasar de una posición\(A\) a otra\(B\) viene dada por lo negativo de la obra\(m\) hecho por la fuerza:\[\begin{aligned} \Delta U = U(r_B) - U(r_A) = -W = G\frac{Mm}{r_A} - G\frac{Mm}{r_B}\end{aligned}\] Por inspección, podemos identificar la función de energía potencial para la gravedad:

\[U(r)=-G\frac{Mm}{r}+C\]

que se determina sólo hasta una constante,\(C\).

Una elección particularmente útil de constante es\(C=0\). Esto corresponde a elegir la energía potencial para que sea cero sólo cuando\(r\) va al infinito. Es decir, la energía potencial de la masa\(m\) es cero sólo cuando está infinitamente lejos de la masa\(M\). La elección de la constante\(C\) corresponde al valor (arbitrario) de la energía potencial cuando la masa\(m\) está infinitamente lejos de la masa\(M\). Cuando la masa no\(m\) está infinitamente lejos, tiene energía potencial negativa (si\(C=0\)). ¡Esto no es un problema! Recuerde, lo único que tiene sentido es una diferencia en la energía potencial, por lo que el valor específico de la energía potencial no tiene sentido. La energía cinética de un objeto, por otra parte, tiene que ser positiva.

Recordemos que si no hay otras fuerzas que actúen sobre un objeto, ese objeto se moverá de tal manera para reducir su energía potencial. Si el objeto de masa\(m\) se ubica a cierta\(r\) distancia del objeto de masa\(M\), la fuerza de la gravedad atraerá\(m\) para que\(r\) disminuya. A\(r\) medida que disminuye en magnitud, la energía potencial se vuelve más negativa (mayor en magnitud, pero más alejada de cero), y la energía potencial de\(m\) efectivamente disminuirá a medida que se acelera debido a la fuerza de la gravedad.

Energía mecánica con gravedad

A menos que se indique lo contrario, continuaremos nuestra discusión sobre la energía potencial gravitacional con la elección particular de la constante\(C=0\):

\[U(r)=-G\frac{Mm}{r}\]

Además, asumiremos que\(M\) es un cuerpo grande, como la Tierra, que podemos considerar como fijo, y enfocaremos nuestra discusión en describir el movimiento de masa\(m\) (por ejemplo, un satélite). Si\(M\) es mucho mayor que\(m\), ambos experimentarán una fuerza de gravedad el uno del otro de la misma magnitud (la Tercera Ley de Newton), pero debido a que\(M\) es mucho mayor, su aceleración será mucho menor (la Segunda Ley de Newton). Así, es una buena aproximación asumir que\(M\) es estacionario y que sólo\(m\) se mueve cuando\(M>>m\).

Podemos definir la energía mecánica total de la masa\(m\) cuando tiene una velocidad\(v\) (relativa a\(M\)) y se ubica a una\(r\) distancia del centro de masa\(M\):\[\begin{aligned} E = U + K = -G\frac{Mm}{r}+\frac{1}{2}mv^2\end{aligned}\] donde el término de energía cinética es siempre positivo. Si la gravedad es la única fuerza que se ejerce sobre la masa\(m\), entonces la energía mecánica\(E\), como se definió anteriormente, será una constante. La energía mecánica de un objeto puede darnos una idea del posible movimiento del objeto.

Imagínese lanzar un cohete recto hacia arriba desde la superficie de la Tierra; una vez que todo el combustible se haya quemado, la energía mecánica del cohete se vuelve constante a medida que el motor del cohete deja de trabajar en el cohete. Tan pronto como el motor deje de proporcionar empuje, el cohete comenzará a disminuir la velocidad a medida que la fuerza de gravedad atrae al cohete de regreso a la Tierra. Si el cohete va lo suficientemente rápido, podrá escapar por completo de la atracción gravitacional de la Tierra y viajar al infinito (suponemos que no hay otros planetas ni el Sol, ¡solo existe la Tierra!). Si, por otro lado, la velocidad del cohete es demasiado baja, eventualmente se detendrá y volverá a caer a la Tierra. Esto es lo mismo que te sucede cuando intentas saltar verticalmente. Si pudieras saltar lo suficientemente fuerte, ¡podrías escapar de la atracción gravitacional de la Tierra!

En términos de energía mecánica, podemos preguntarnos si la energía mecánica del cohete es lo suficientemente grande como para escapar de la atracción gravitacional de la Tierra. En concreto, podemos preguntarnos cuál sería el valor de la energía cinética del cohete cuando llegue al infinito. La energía cinética del cohete viene dada por:\[\begin{aligned} K = E - U\end{aligned}\] Si el cohete está infinitamente lejos de la Tierra, entonces su energía potencial es cero, y la energía cinética es igual a\(E\).

Si la energía mecánica,\(E\), es negativa, no es posible que el cohete llegue alguna vez al infinito porque su energía cinética tendría que ser negativa. En otras palabras, si la energía mecánica es negativa, entonces el objeto de masa nunca\(m\) podrá escapar de la atracción gravitacional del objeto\(M\). Decimos que\(m\) está “ligado gravitacionalmente” a\(M\).

Si la energía mecánica,\(E\), es exactamente cero, entonces la energía cinética del objeto se convertirá en cero justo cuando alcance el infinito. En otras palabras, apenas podrá escapar de la atracción gravitacional de la masa\(M\). La condición para que esto suceda es:\[\begin{aligned} E &= 0\\ K & = -U\\ \frac{1}{2}mv^2 &= G\frac{Mm}{r}\\ \therefore v_{esc} &= \sqrt{\frac{2GM}{r}}\end{aligned}\] que podemos interpretar como una condición para la velocidad del cohete. Si a cierta\(r\) distancia de\(M\), el cohete tiene la velocidad dada por la condición anterior, entonces tendrá suficiente energía cinética para escapar de la atracción gravitacional de\(M\). Llamamos a esta velocidad la “velocidad de escape”.

Por último, si la energía mecánica es mayor que cero, entonces el cohete tendrá suficiente energía para escapar de la atracción gravitacional de\(M\) y tener una velocidad distinta de cero cuando llegue al infinito.

Ejercicio\(\PageIndex{1}\)

¿Cuál es la velocidad de escape de la superficie de la Tierra?

1. \(4.29\times 10^{6}\text{km/s}\)
2. \(1.25\times 10^{5}\text{km/s}\)
3. \(11.2\times{km/s}\)
4. \(9.81\times{km/s}\)

Responder

Ejemplo\(\PageIndex{1}\)

Mostrar que un objeto de masa\(m\) in a circular orbit of radius \(r\) around a body of mass \(M\) has half of the kinetic energy required to escape the gravitational pull of \(M\).

Solución:

La única fuerza que actúa sobre el objeto es la gravedad, por lo que tiene una energía mecánica dada por:\[\begin{aligned} E&=U+K\\ E&=-G\frac{Mm}{r}+\frac{1}{2}mv^2\end{aligned}\] Para que el objeto simplemente escape de la atracción gravitacional de\(M\), su energía mecánica debe ser igual a cero:\[\begin{aligned} E&=0\\ \therefore K_{esc}&=-U\end{aligned}\] Dado que el objeto está en una órbita circular, podemos usar la de Newton Segunda Ley para encontrar una expresión para\(v^2\):\[\begin{aligned} F_{net}&=\frac{mv^2}{r}\\ \frac{GMm}{r^2}&=\frac{mv^2}{r}\\ \frac{GM}{r}&=v^2\end{aligned}\] donde en la segunda línea utilizamos el hecho que\(F_{net}\) es igual a la fuerza de gravedad ejercida por\(M\) sobre el objeto. La energía cinética del objeto es así:\[\begin{aligned} K&=\frac{1}{2}mv^2\\ K&=\frac{1}{2}\frac{GMm}{r}\end{aligned}\] Notarás que esto es muy similar a nuestra expresión para\(U\). De hecho, tenemos:\[\begin{aligned} K&=-\frac{1}{2}U\\ \therefore K&=\frac{1}{2}K_{esc}\end{aligned}\]

Nota:

También podemos ver que la velocidad de un objeto en órbita circular es igual a\(\sqrt{GM/r}\), que es la mitad de la velocidad de escape,\(v_{esc}=\sqrt{2GM/r}\)

Tipos de órbitas

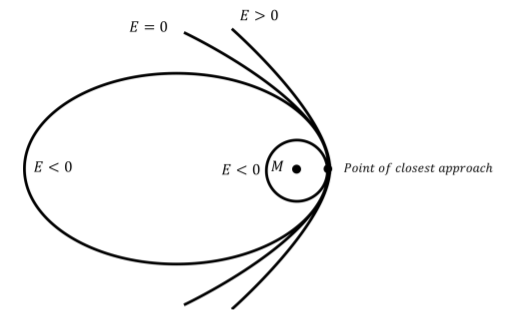
La energía mecánica de un cuerpo de masa\(m\) determina si está ligado gravitacionalmente (es decir, no puede escapar) al cuerpo de masa\(M\). El camino (órbita) que\(m\) tomará depende de su velocidad con respecto a\(M\). Claramente, si la velocidad de\(m\) se dirige al centro de\(M\), entonces simplemente\(m\) chocará con\(M\). En todos los demás casos, la órbita que\(m\) tomará depende de la energía mecánica de así\(m\) como de la velocidad de\(m\) en el punto de aproximación más cercano a\(M\) (ver Figura\(\PageIndex{2}\)). La velocidad de\(m\) en el punto de aproximación más cercana siempre será perpendicular a la línea que une los centros de\(m\) y\(M\). Las diferentes órbitas posibles son:

1. Una órbita circular de radio\(R\) (donde\(R\) está la distancia de aproximación más cercana) si la energía mecánica es negativa (es decir, está ligada) y la velocidad es exactamente igual al valor necesario para que la fuerza gravitacional proporcione lo requerido aceleración centrípeta para un movimiento circular uniforme:\[\begin{aligned} \sum F = G\frac{Mm}{R^2} &= m\frac{v^2}{R}\\ \therefore v_{circ}=\sqrt{\frac{GM}{R}}\end{aligned}\]
2. Una órbita elíptica si la energía mecánica es negativa y la velocidad en el punto de aproximación más cercano es diferente a la requerida para una órbita circular.
3. Una órbita parabólica si la energía mecánica es exactamente cero.
4. Una órbita hiperbólica si la energía mecánica es mayor que cero.

Las posibles órbitas se ilustran en la Figura\(\PageIndex{2}\), y son curvas de la familia de “secciones cónicas”, ya que se pueden encontrar por la intersección de un plano y un cono. Todas las secciones cónicas tienen al menos un punto de “enfoque” (las elipses tienen dos) que corresponde a la ubicación de\(M\).

Figura\(\PageIndex{2}\): Las diferentes órbitas posibles de\(m\) debido a la fuerza gravitacional de\(M\) dependen de la energía mecánica,\(E\), de\(m\). Las órbitas se dibujan en un marco de referencia donde\(M\) está en reposo.