10.2: Colisiones

En esta sección vamos a través de algunos ejemplos de aplicación de conservación de impulso a colisiones de modelos. Las colisiones pueden definirse vagamente como eventos en los que los momentos de las partículas individuales en un sistema son diferentes antes y después del evento.

Distinguimos entre dos tipos de colisiones: colisiones elásticas e inelásticas. Las colisiones elásticas son aquellas para las que la energía mecánica total del sistema se conserva durante la colisión (es decir, es la misma antes y después de la colisión). Las colisiones inelásticas son aquellas para las que no se conserva la energía mecánica total del sistema. En cualquier caso, para modelar el sistema, se elige definir el sistema de tal manera que no haya fuerzas externas en el sistema para que se conserve el impulso total.

Colisiones inelásticas

En esta sección, damos algunos ejemplos de modelización de colisiones inelásticas. Las colisiones inelásticas suelen ser más fáciles de manejar matemáticamente, porque solo se necesita considerar la conservación del impulso y no se usa la conservación de energía (lo que generalmente implica ecuaciones que son cuadráticas en las velocidades debido al término de energía cinética).

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{1}\): Un patinador empujando a otro sobre una superficie horizontal sin fricción.

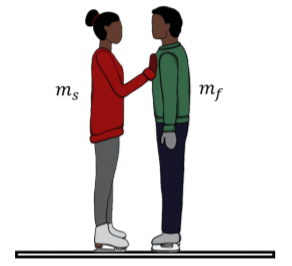
Usted (misa\(m_s\)) and your friend (mass \(m_f\)) face each other on ice skates on an ice surface that is slippery enough that friction can be considered negligible, as shown in Figure \(\PageIndex{1}\). You shove your friend away from you so that he moves with velocity \(\vec v_f\) away from you (the velocity is measured relative to the ice). Is the collision elastic? What is your speed relative to the ice after you shoved your friend?

Solución:

Podemos considerar que el sistema está compuesto por usted y su amigo. No hay fuerzas externas netas en el sistema (la gravedad y las fuerzas normales se cancelan entre sí), por lo que se conservará el impulso del sistema.

No se conservará la energía mecánica. Tenías que usar la energía potencial química almacenada en tus músculos para empujar a tu amigo. Así, se inyectó energía externa (es decir, no energía mecánica de usted o de su amigo) en el sistema, y debemos esperar que la energía mecánica total sea mayor después de la colisión.

Antes de la colisión, tanto tú como tu amigo tienen velocidad cero, y por lo tanto cero energía cinética y cero impulso. Después de la colisión, tu amigo tiene una velocidad\(\vec v_f\). Podemos utilizar la conservación del momento total,\(\vec P\), para determinar su velocidad,\(\vec v_s\), después de la colisión. \[\begin{aligned} \vec P &=\vec P'\\ 0 &= m_s\vec v_s + m_f\vec v_f\\ \therefore \vec v_s &= -\frac{m_f}{m_s}\vec v_f\end{aligned}\]donde los primos (\('\)) denotan una cantidad después de la colisión. Encontramos que tu velocidad es en sentido contrario a la de tu amigo. Antes de la colisión, la energía mecánica\(E\),, del sistema es cero (podemos ignorar la energía potencial gravitacional, ya que todo está en el plano horizontal). Después de la colisión, la energía mecánica,\(E'\), es:\[\begin{aligned} E' = \frac{1}{2}m_sv_s^2+\frac{1}{2}m_fv_f^2\end{aligned}\] que es claramente mayor que la energía mecánica antes de la colisión (es decir, 0), como sospechábamos que sería.

Discusión:

Nos encontramos con que se da un retroceso en sentido contrario, lo cual tiene sentido. Si empujas a tu amigo en una dirección, la Tercera Ley de Newton dice que tu amigo te empuja en dirección opuesta. Tu velocidad depende además de la relación entre la masa de tu amigo y la tuya. Esto también tiene sentido, porque si ambos sienten la misma fuerza, la persona con la masa más pequeña tendrá la velocidad más alta; si tu masa es mayor que la de tu amigo, entonces tu velocidad después de la colisión será menor que la de tu amigo.

También vimos que la energía mecánica no se conservaba. En términos de energía, podemos explicar esto diciendo que quemaste energía potencial química almacenada en tus músculos para empujar a tu amigo. Debido a que incluimos tanto a usted como a su amigo en el sistema, el empujón era una fuerza interna y se conserva el impulso. Por supuesto, si hubiéramos considerado solo a usted como el sistema, entonces su impulso no se habría conservado durante la colisión.

El tipo de colisión que describimos aquí también a veces se llama “explosión”. Se pueden imaginar todas las partes que componen una bomba como pequeñas partículas. Cuando la bomba explota, la energía potencial química se convierte en la energía cinética de los fragmentos de la bomba. Si considera todas las partículas/fragmentos de la bomba como un sistema, entonces se conserva el impulso total de todos los fragmentos de bomba (e igual a cero si la bomba estaba inicialmente en reposo). Nuevamente, la energía mecánica no se conservaría (y aumentaría) a medida que la energía potencial química se convierte en energía mecánica.

Ejemplo\(\PageIndex{2}\)

Un protón de masa\(m_p\) and initial velocity \(\vec v_p\) collides inelastically with a nucleus of mass \(m_N\) at rest, as shown in Figure \(\PageIndex{2}\). A coordinate system is set up as shown, such that the initial velocity of the proton is in the \(x\) direction. After the collision, the proton’s speed is measured to be \(v'_p\) and its velocity vector is found to make an angle \(\theta\) with the \(x\) axis as shown. What is the velocity vector of the nucleus after the collision? Assume that the collision takes place in vacuum.

Figura\(\PageIndex{2}\): Un protón de masa\(m_{p}\) colisionando inelásticamente con un núcleo de masa\(m_{N}\).

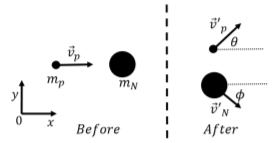
Solución:

Como sistema, consideramos el protón y el núcleo juntos, de manera que el impulso total del sistema se conserva durante la colisión, ya que no se ejercen otras fuerzas externas sobre las dos partículas (ya que están en vacío). Debido a que el impulso es un vector, cada componente del impulso total,\(\vec P\), se conserva durante la colisión:\[\begin{aligned} \vec P &= \vec P'\\ \therefore P_x &= P'_x\\ \therefore P_y &= P'_y\end{aligned}\] donde, como de costumbre, los primos (\('\)) denotan cantidades después de la colisión. Después de la colisión, ambas partículas tendrán vectores de velocidad que tienen\(x\) y\(y\) componentes. Dejar ser el vector de velocidad del núcleo después de la colisión\(\vec v'_N\) y dejar\(\phi\) ser el ángulo que hace con el\(x\) eje, como se muestra en la Figura\(\PageIndex{2}\).

Podemos comenzar considerando la conservación del\(x\) componente del impulso total. Los momentos inicial y final en la\(x\) dirección vienen dados por:\[\begin{aligned} P_x &= m_p v_p\\ P'_x &= m_p v'_p\cos\theta + m_N v'_N\cos\phi\\ \therefore m_p v_p &= m_p v'_p\cos\theta + m_N v'_N\cos\phi\end{aligned}\] lo que nos da una primera ecuación para determinar la velocidad final del núcleo.

El\(y\) componente del impulso total antes de la colisión es cero ya que elegimos el sistema de coordenadas de tal manera que la velocidad inicial del protón está en la\(x\) dirección. Los momentos inicial y final en la\(y\) dirección vienen dados por:\[\begin{aligned} P_y &= 0\\ P'_y &= m_p v'_p\sin\theta - m_N v'_N\sin\phi\\ \therefore m_p v'_p\sin\theta &= m_N v'_N\sin\phi\end{aligned}\] lo que nos da una segunda ecuación para resolver para la velocidad del núcleo. Con las dos ecuaciones de conservación del momento, podemos resolver por la magnitud y dirección de la velocidad del núcleo. A partir del\(y\) componente de conservación del impulso, podemos encontrar una expresión para la velocidad del núcleo: la\[\begin{aligned} m_p v'_p\sin\theta &= m_N v'_N\sin\phi\\ \therefore v'_N &= \frac{m_p}{m_N}v'_p\sin\theta \frac{1}{\sin\phi}\end{aligned}\] cual podemos sustituir en la\(x\) ecuación para la conservación del impulso para resolver por el ángulo\(\phi\):\[\begin{aligned} m_p v_p &= m_p v'_p\cos\theta + m_N v'_N\cos\phi\\ m_p v_p &= m_p v'_p\cos\theta + m_N\frac{m_p}{m_N}v'_p\sin\theta \frac{\cos\phi}{\sin\phi} \\ v_p &= v'_p\cos\theta + v'_p\sin\theta \frac{1}{\tan\phi}\\ \therefore \tan\phi &= \frac{v'_p\sin\theta}{v_p-v'_p\cos\theta}\end{aligned}\] Si nos dieran números para la velocidad inicial y final del protón, así como el ángulo\(\theta\), podríamos encontrar un valor para el ángulo\(\phi\), que luego podríamos usar para determinar la velocidad final del núcleo:\[\begin{aligned} v'_N &= \frac{m_p}{m_N}v'_p\sin\theta \frac{1}{\sin\phi}\end{aligned}\] Discusión:

Al usar la ecuación de conservación de momento y escribir\(y\) los componentes\(x\) y, pudimos encontrar dos ecuaciones para determinar la magnitud y dirección de la velocidad del núcleo después de la colisión. En el límite donde\(m_N >> m_p\), la velocidad final del núcleo sería muy pequeña (cercana a cero).

Colisiones elásticas

En esta sección, damos algunos ejemplos de modelado de colisiones elásticas. A pesar de que es la energía mecánica la que se conserva en una colisión elástica, casi siempre se puede simplificar esto para que solo se conserve la energía cinética. Si una colisión tiene lugar en una posición bien localizada en el espacio (es decir, antes y después de la colisión son el mismo punto en el espacio), entonces las energías potenciales de los objetos involucrados no cambiarán, por lo que cualquier cambio en su energía mecánica se debe a un cambio en la energía cinética.

Ejemplo\(\PageIndex{3}\)

Figura\(\PageIndex{3}\): Dos bloques a punto de colisionar elásticamente.

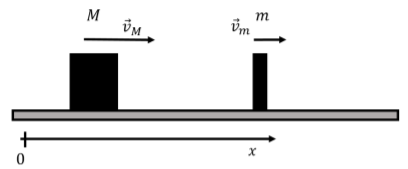
Un bloque de masa\(M\) moves with velocity \(\vec v_M\) in the \(x\) direction, as shown in Figure \(\PageIndex{3}\). A block of mass \(m\) is moving with velocity \(\vec v_m\) also in the \(x\) direction and collides elastically with block \(M\). Both blocks slide with no friction on the horizontal surface. What are the velocities of the two blocks after the collision?

Solución:

Debido a que se trata de una colisión elástica, se conservan tanto el impulso total como la energía mecánica total. Equiparar el impulso total antes y después de la colisión, y considerando solo el\(x\) componente, da la siguiente ecuación:\[\begin{aligned} \vec P &=\vec P'\\ Mv_M+mv_m&=Mv'_M+mv'_m\end{aligned}\] donde los primos (\('\)) corresponden a las cantidades posteriores a la colisión. Obsérvese que, en principio, los\(x\) componentes de las velocidades (\(v_M\)\(v'_M\),\(v_m\),,\(v'_m\)) podrían ser números negativos si el bloque correspondiente se mueve en la\(x\) dirección negativa.

Para la energía mecánica de los dos bloques, solo necesitamos considerar su energía cinética ya que sus energías potenciales gravitacionales son las mismas antes y después de la colisión en la superficie horizontal. La energía mecánica total del sistema, antes y después de la colisión viene dada por:\[\begin{aligned} E &=E'\\ \frac{1}{2}Mv_M^2+\frac{1}{2}mv_m^2&=\frac{1}{2}Mv'^2_M+\frac{1}{2}mv'^2_m\\ \therefore Mv_M^2+mv_m^2&=Mv'^2_M+mv'^2_m\end{aligned}\] donde cancelamos el factor de la mitad en la última línea. Esto da dos ecuaciones (conservación de energía e impulso) y dos incógnitas (las dos velocidades después de la colisión). Este no es un sistema lineal de ecuaciones, porque la ecuación de conservación de energía es cuadrática en las velocidades.

El siguiente método permite resolver fácilmente muchos modelos de colisiones elásticas entre dos partículas convirtiendo la ecuación cuadrática de conservación de energía en una ecuación lineal en las velocidades. Primero, escribe ambas ecuaciones para que las cantidades relacionadas con cada partícula estén en lados opuestos de la ecuación. Para el impulso, esto da:

\[Mv_{M}+mv_{m}=Mv_{M}^{'} +mv_{m}^{'}\]

\[\therefore M(v_{M}-v_{M}^{'})=m(v'm-v_{m})\]

Para la conservación de la energía, esto da:

\[Mv_{M}^{2}+mv_{m}^{2}=Mv_{M}^{'2}+mv_{m}^{'2}\]

\[\therefore M(v_{M}^{2}-v_{M}^{'2}=M(v_{m}^{'2}-v_{m}^{2})\]

que podemos reescribir como:

\[\begin{aligned} M(v_M^2-v'^2_M)&= M(v'^2_m-v^2_m)\\ M(v_M-v'_M)(v_M+v'_M)&= M(v'_m-v_m)(v'_m+v_m)\end{aligned}\]

Entonces podemos dividir la Ecuación 10.2.3 y 10.2.4 por la Ecuación 10.2.1 y 10.2.2:\[\begin{aligned} \frac{M(v_M-v'_M)(v_M+v'_M)}{M(v_M-v'_M)}&= \frac{M(v'_m-v_m)(v'_m+v_m)}{m(v'm-v_m)}\\ \therefore v_M+v'_M&=v'_m+v_m\end{aligned}\] lo que nos da una ecuación que es mucho más fácil de trabajar, ya que es lineal en las velocidades. Si reorganizamos esta última ecuación de manera que las cantidades antes y después de la colisión estén en diferentes lados de la igualdad:

\[v_{M}-v_{m}=-(v_{M}^{'}-v_{m}^{'})\]

podemos ver que la velocidad relativa entre\(M\) y\(m\) es la misma antes y después de la colisión. Es decir, si el bloque\(M\) “vio” el bloque que\(m\) se aproximaba con una velocidad de\(3\text{m/s}\) antes de la colisión, “vería” el bloque\(m\) alejándose con la velocidad\(3\text{m/s}\) después de la colisión, independientemente de la real direcciones y velocidades del bloque, si la colisión fue elástica.

Al usar esta ecuación con la ecuación original de conservación del momento, ahora tenemos dos ecuaciones y dos incógnitas que son fáciles de\[\begin{aligned} v_M-v_m &= - (v'_M-v'_m)\\ Mv_M+mv_m&=Mv'_M+mv'_m\end{aligned}\] resolver: Resolver for\(v'_m\) en ambas ecuaciones da:\[\begin{aligned} v_M-v_m &= - (v'_M-v'_m)\\ \therefore v'_m &= v_M+v'_M-v_m\\ Mv_M+mv_m&=Mv'_M+mv'_m\\ \therefore v'_m&=\frac{1}{m}(Mv_M+mv_m-Mv'_M)\end{aligned}\] Equiparar las dos expresiones para nos\(v'_m\) permite resolver para \(v'_M\):\[\begin{aligned} \frac{1}{m}(Mv_M+mv_m-Mv'_M)&=v_M+v'_M-v_m\\ Mv_M+mv_m-Mv'_M&=mv_M+mv'_M-mv_m\\ (M-m)v_M+2mv_m&=(M+m)v'_M\\ \therefore v'_M&=\frac{M-m}{M+m}v_M+\frac{2m}{M+m}v_m\end{aligned}\] Uno puede resolver fácilmente para la otra velocidad,\(v'_m\):\[\begin{aligned} \therefore v'_m &= \frac{m-M}{M+m}v_m+\frac{2M}{M+m}v_M\end{aligned}\] Y escribiendo estos juntos:\[\begin{aligned} v'_M&=\frac{M-m}{M+m}v_M+\frac{2m}{M+m}v_m\\ v'_m &= \frac{m-M}{M+m}v_m+\frac{2M}{M+m}v_M\end{aligned}\]

Discusión:

Las fórmulas que hemos obtenido anteriormente son válidas para cualquier colisión elástica unidimensional.

Ejercicio\(\PageIndex{1}\)

Dos trenes de masas iguales chocan elásticamente en una vía. Si entrenar\(A\) had a speed \(v\) and train \(B\) was at rest, what are the speeds of the trains after the collision?

1. \(A\)Tanto los trenes como los\(B\) viajes alejados unos de otros con velocidades\(\frac{1}{2}v\).
2. \(A\)El tren estará en reposo y el tren\(B\) se alejará con una velocidad\(v\).
3. Ambos trenes\(A\) y\(B\) se quedarán unidos y se moverán a una velocidad de\(v\).
4. \(B\)El tren estará en reposo y el tren\(A\) se alejará a una velocidad de\(v\).

Responder

Ejemplo\(\PageIndex{4}\)

Figura\(\PageIndex{4}\): Un protón choca elásticamente con un protón en reposo.

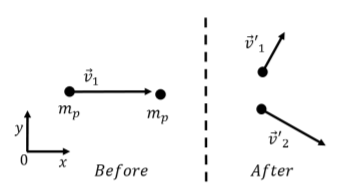
Un protón de masa\(m\) and initial velocity \(\vec v_1\) collides elastically with a second proton that is at rest. After the collision, the two protons have velocities \(\vec v'_1\) and \(\vec v'_2\), as shown in Figure \(\PageIndex{4}\). Show that the velocity vectors of the two protons are perpendicular after the collision.

Solución:

En este ejemplo se resalta una característica particular de las colisiones elásticas cuando los dos objetos tienen la misma masa y uno de los objetos está inicialmente en reposo. La conservación del impulso para el sistema compuesto por los dos protones puede escribirse como:\[\begin{aligned} m\vec v_1 &= m\vec v'_1 + m\vec v'_2\\ \vec v_1 &= \vec v'_1 + \vec v'_2\end{aligned}\] donde el lado izquierdo corresponde al impulso total inicial y el lado derecho al impulso total después de la colisión. En la segunda línea, cancelamos la masa y obtuvimos una relación vectorial entre los vectores de velocidad. Podemos ilustrar gráficamente la relación vectorial como en la Figura\(\PageIndex{5}\) que muestra el triángulo que se forma sumando los dos vectores de velocidad de salida para obtener el vector de velocidad inicial.

Figura\(\PageIndex{5}\): Ilustración gráfica de la relación entre los vectores de velocidad inicial y final como suma vectorial.

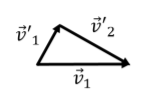
La conservación de la energía cinética para la colisión se puede escribir como:\[\begin{aligned} \frac{1}{2}mv_1^2 &= \frac{1}{2}mv'^2_1+\frac{1}{2}mv'^2_2\\ v_1^2 &= v'^2_1+ v'^2_2\end{aligned}\] donde el lado izquierdo corresponde a la energía cinética inicial y el lado derecho a la energía cinética final. Cancelamos la masa y factor de la mitad en la segunda línea. Esta última ecuación da una relación entre las magnitudes de los vectores de velocidad. Al comparar la ecuación anterior con el teorema de Pitágoras, y al inspeccionar el triángulo en la Figura\(\PageIndex{5}\), queda claro que el triángulo debe ser un triángulo de ángulo recto, y así ese\(\vec v'_1\) y\(\vec v'_2\) debe ser perpendicular.

Marcos de referencia

revisar temas

Antes de continuar, es posible que desee revisar las Secciones 3.4 y 4.1 sobre la expresión de velocidades en diferentes marcos de referencia.

Debido a que el momento de una partícula se define usando la velocidad de la partícula, su valor depende del marco de referencia en el que elegimos medir esa velocidad. En algunos casos, es útil aplicar la conservación del impulso en un marco de referencia donde el impulso total del sistema es cero. Por ejemplo, consideremos dos partículas de masa\(m_1\) y\(m_2\), moviéndose una hacia la otra con velocidades\(\vec v_1\) y\(\vec v_2\), respectivamente, según se mide en un marco de referencia\(S\), como se ilustra en la Figura 10.2.6.

Figura\(\PageIndex{6}\): Dos partículas moviéndose una hacia la otra.

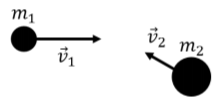
En el marco de referencia\(S\), se puede escribir el momento total\(\vec P\),, de las dos partículas:\[\begin{aligned} \vec P = m_1\vec v_1 + m_2\vec v_2\end{aligned}\] Considere un marco de referencia\(S'\),, que se mueve con velocidad\(\vec v_{CM}\),, relativo al marco de referencia \(S\). En ese marco de referencia, las velocidades de las dos partículas son diferentes y están dadas por:\[\begin{aligned} \vec v'_1&=\vec v_1- \vec v_{CM}\\ \vec v'_2&=\vec v_2- \vec v_{CM}\end{aligned}\]

El impulso total,\(\vec P'\), en el marco de referencia\(S'\) viene dado entonces por ¹:

\[\begin{aligned} \vec P' &= m_1\vec v'_1 + m_2 \vec v'_2\\ &=m_1(\vec v_1- \vec v_{CM})+m_2(\vec v_2- \vec v_{CM})\\ &= m_1\vec v_1 + m_2\vec v_2 - (m_1+m_2) \vec v_{CM}\end{aligned}\]

Podemos elegir la velocidad del cuadro\(S'\)\(\vec v_{CM}\), de tal manera que el impulso total en ese marco de referencia sea cero:\[\begin{aligned} \vec P' &= 0\\ m_1\vec v_1 + m_2\vec v_2 - (m_1+m_2) \vec v_{CM} &=0\\ \therefore \vec v_{CM} &= \frac{m_1\vec v_1 + m_2\vec v_2 }{m_1+m_2}\end{aligned}\]

Este marco de referencia “especial”, en el que el impulso total del sistema es cero, se denomina “marco de referencia del centro de masa”. La velocidad del marco de referencia del centro de masa se puede obtener fácilmente si hay\(N\) partículas involucradas en lugar de dos:

\[\therefore \vec v_{CM}=\frac{m_{1}\vec v_{1}+m_{2}\vec v_{2}+m_{3}\vec v_{3}+...}{m_{1}+m_{2}+m_{3}+...}=\frac{\sum m_{i}\vec v_{i}}{\sum m_{i}}\]

Nuevamente, hay que señalar que debido a que la ecuación anterior es una ecuación vectorial, representa una ecuación por componente de los vectores. Por ejemplo, el\(x\) componente de la velocidad del marco de referencia del centro de masa viene dado por:\[\begin{aligned} \therefore v_{CMx} = \frac{m_1 v_{1x} + m_2v_{2x} + m_3 v_{3x} + \dots }{m_1+m_2+m_3+\dots}=\frac{\sum m_iv_{ix}}{\sum m_i}\end{aligned}\]

Ejemplo\(\PageIndex{5}\)

Figura\(\PageIndex{7}\): Un bloque que se aproxima a otro bloque idéntico en reposo, como se ve en el marco de referencia del laboratorio.

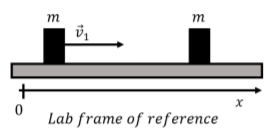
En el marco de referencia de un laboratorio, un bloque de masa\(m\) has a velocity \(\vec v_1\) directed along the positive \(x\) axis and is approaching a second block of mass \(m\) that is at rest (\(\vec v_2=0\)), as shown in Figure \(\PageIndex{7}\). What is the velocity of the center of mass frame? What is the velocity of each block in the center of mass frame? Verify that the total momentum is zero in the center of mass frame.

Solución:

Dado que se trata de una situación unidimensional, solo necesitamos evaluar el\(x\) componente de la velocidad del centro de masa:\[\begin{aligned} \vec v_{CM} &= \frac{m_1\vec v_1 + m_2\vec v_2 }{m_1+m_2}\\ \therefore v_{CMx} &= \frac{m_1 v_{1x} + m_2 v_{2x}}{m_1+m_2}\\ &=\frac{mv_1 + m(0) }{m+m}\\ &=\frac{1}{2}v_1\end{aligned}\]

El marco de referencia del centro de masa también se mueve a lo largo de la dirección positiva\(x\) del eje, pero con una velocidad que es la mitad de la del bloque móvil. En el marco de referencia del centro de masa, parece que el bloque de la izquierda es más lento que en el marco de laboratorio y que el bloque de la derecha se mueve en\(x\) dirección negativa. Las velocidades de los dos bloques en el marco de referencia del centro de masa vienen dadas por:

\[\begin{aligned} v'_1&=v_1-v_{CMx}=\frac{1}{2}v_1\\ v'_2&=(0)-v_{CMx}=-\frac{1}{2}v_1\end{aligned}\]

Así, en el marco de referencia del centro de masa, los dos bloques se acercan entre sí con la misma velocidad (\(v_1/2\)), lo que es sólo el caso porque los dos bloques tienen la misma masa. Los bloques, tal como se ve en el marco de referencia del centro de masa, se muestran en la Figura\(\PageIndex{8}\).

Figura\(\PageIndex{8}\): En el marco de referencia del centro de masa, el bloque se aproxima entre sí con la misma velocidad, porque tienen la misma masa.

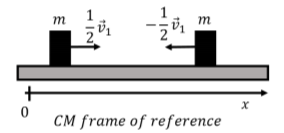
Claramente, el impulso total es cero en el marco de referencia del centro de masa:

\[\begin{aligned} \vec P' = m\vec v'_1+ m\vec v'_2 = m \left(\frac{1}{2}\vec v_1 - \frac{1}{2}\vec v_1\right) = 0\end{aligned}\]

Discusión:

Como hemos visto, en el centro de masa marco de referencia el impulso total es cero. Si sólo hay dos partículas, y tienen la misma masa, entonces, en el centro de masa marco de referencia, ambas tienen la misma velocidad y se mueven acercándose o alejándose una de la otra.

Notas al pie

1. Tenga en cuenta que estamos usando primes (\('\)) para denotar cantidades en un marco de referencia diferente, no después de una colisión.