10.6: Problemas y soluciones de la muestra

Ejercicio\(\PageIndex{1}\)

Figura\(\PageIndex{1}\): Una bala de masa\(m\) golpea y se incrusta en un péndulo balístico de masa\(M\).

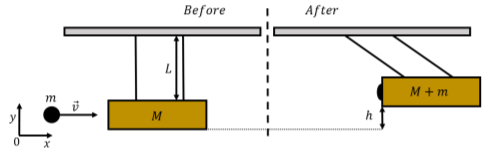
Un péndulo balístico es un dispositivo que se puede construir para medir la velocidad de un proyectil. El péndulo se construye de tal manera que el proyectil se dispara contra el bob del péndulo (típicamente un bloque de madera) que luego se balancea como se ilustra en la Figura\(\PageIndex{1}\), with the projectile embedded within. By measuring the height that is reached by the pendulum’s bob, one can determine the speed of the projectile before it collided with the pendulum. If a ballistic pendulum with a mass \(M\) suspended at the end of strings of length \(L\) is observed to rise by a height \(h\) after being struck by a bullet of mass \(m\), how fast was the bullet moving?

Contestar

Podemos modelar esta situación dividiéndola en tres fases:

1. Antes de que la bala colisione con el péndulo, sólo la bala tiene impulso en la\(x\) dirección.
2. Inmediatamente después de la colisión inelástica, la bala y el péndulo forman un objeto combinado de masa\(M+m\) que tiene el mismo impulso que la bala, en la\(x\) dirección, antes de que el péndulo comience a balancearse hacia arriba.
3. El péndulo con la bala incrustada oscila hacia arriba hasta que su energía cinética es cero.

La colisión entre la bala y el péndulo es inelástica, debido a que parte de la energía cinética de la bala se utiliza para deformar la bala y el péndulo. En general, cualquier colisión donde dos objetos terminen “pegados” es inelástica.

Para modelar el movimiento del péndulo primero aplicamos la conservación del momento para determinar la velocidad,\(v'\), del péndulo y la bala incrustada justo después de la colisión. Aplicando la conservación del impulso en la\(x\) dirección al sistema formado por el péndulo y la bala, justo antes y después de la colisión, tenemos:

\[\begin{aligned} P&=mv \\ P'&=(M+m)v' \\ \therefore mv&=(M+m)v' \\ \therefore v' &=\frac{m}{m+M}v \end{aligned}\]

donde\(P\) y\(P'\) son los momentos inicial y final del sistema, respectivamente. El péndulo con la bala incrustada en él tendrá así una velocidad de\(v'\) en la parte inferior del movimiento del péndulo, antes de que oscile hacia arriba.

Ahora podemos usar la conservación de energía para modelar el movimiento oscilante ya que, en ese punto, solo la tensión y la gravedad actúan sobre el péndulo, y no hay fuerzas no conservadoras. Si elegimos que el origen sea la ubicación del péndulo en el fondo de su trayectoria, su energía potencial gravitacional inicial es cero y su energía mecánica inicial,\(E\), viene dada por:

\[\begin{aligned} E = \frac{1}{2}(m+M) v'^2 \end{aligned}\]

En la parte superior de la trayectoria, el péndulo con la bala incrustada se detendrá y no tendrá energía cinética. La energía mecánica en la parte superior de la trayectoria\(E'\),, es así igual a la energía potencial gravitacional del péndulo a una altura\(h\) por encima del origen:

\[\begin{aligned} E' = (m+M)gh\end{aligned}\]

Aplicar conservación de energía mecánica nos permite encontrar la velocidad inicial de la bala:

\[\begin{aligned} E &= E'\\ \frac{1}{2}(m+M) v'^2 &= (m+M)gh\\ v'^2 &= 2gh\\ \left( \frac{m}{m+M}v\right)^2&= 2gh\\ \therefore v &= \frac{m+M}{m} \sqrt{2gh}\end{aligned}\]

donde está la segunda última línea que utilizamos la expresión para la\(v'\) que obtuvimos de la conservación del impulso.

Discusión:

Este ejemplo mostró una situación en la que tanto el impulso como la energía se conservaron, pero no al mismo tiempo. Este ejemplo también resaltó cómo, mediante el uso de leyes de conservación, se pueden derivar modelos que son mucho más fáciles de resolver matemáticamente que si uno tuviera que modelar todas las fuerzas involucradas.

Ejercicio\(\PageIndex{2}\)

Figura\(\PageIndex{2}\): Un bloque unido a un muelle a punto de chocar con otro bloque.

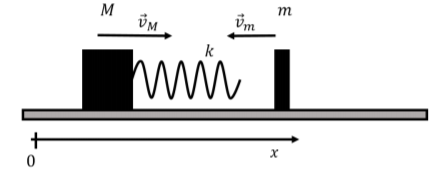
Un bloque de masa\(M\) with a spring of spring constant \(k\) attached to it is sliding on a frictionless surface with velocity \(\vec v_M\) in the \(x\) direction. A second block of mass \(m\) has velocity \(\vec v_m\) also in the \(x\) direction (shown above in the negative \(x\) direction, but let us assume that we do not necessarily know the direction, only that the two blocks will collide). During the collision between the blocks, what is the maximum amount by which the spring is compressed?

Contestar

La colisión es elástica porque la energía utilizada para comprimir el resorte se “devuelve” cuando el resorte se extiende nuevamente, ya que la fuerza del resorte es conservadora.

Ellos clave para modelar la compresión del resorte es identificar la condición bajo la cual el resorte se comprime al máximo. Esto ocurrirá en el punto durante la colisión donde las dos masas tendrán exactamente la misma velocidad, moviéndose momentáneamente al unísono a medida que el resorte se comprime al máximo. Porque, instantáneamente, las masas tienen la misma velocidad, hay un marco de referencia en el que las dos masas están en reposo, y el impulso es cero. Por supuesto, ese marco de referencia es el marco de referencia del centro de masa.

Debido a que la colisión es unidimensional, podemos calcular la velocidad del centro de masa como:\[\begin{aligned} v_{CM} = \frac{Mv_M+mv_m}{m+M}\end{aligned}\] donde observamos que\(v_m\) es un número negativo, ya que el bloque de masa\(m\) se mueve en la\(x\) dirección negativa. El impulso total,\(\vec P^{CM}\), en el centro de masa marco de referencia debe ser cero. Escribiendo esto para el\(x\) componente y transformando las velocidades de los dos bloques en el marco de referencia del centro de masa:

\[\begin{aligned} P^{CM}_x = M(v_M-v_{CM})+m(v_m-v_{CM})&=0\\ \therefore (v_m-v_{CM}) &= -\frac{M}{m}(v_M-v_{CM})\end{aligned}\]

También tenga en cuenta que podemos escribir la diferencia de velocidad\(v_M-v_{CM}\) sin usar la velocidad del centro de masa: Luego\[\begin{aligned} v_M-v_{CM} &= v_M-\frac{Mv_M+mv_m}{m+M}=\frac{1}{m+M}(v_M(m+M)-Mv_M-mv_m)\\ &=\frac{m}{m+M}(v_M-v_m)\end{aligned}\] podemos usar la conservación de energía en el marco del centro de masa para determinar la compresión máxima del resorte. Antes de la colisión, la energía mecánica total en el sistema,\(E\), es la suma de las energías cinéticas de los dos bloques (ya que el resorte no está comprimido):

\[\begin{aligned} E&=\frac{1}{2}m(v_m-v_{CM})^2+\frac{1}{2}M(v_M-v_{CM})^2\\ &=\frac{1}{2}\frac{M^2}{m}(v_M-v_{CM})^2+\frac{1}{2}M(v_M-v_{CM})^2\\ &=\frac{1}{2}M \left( 1 + \frac{M}{m}\right) (v_M-v_{CM})^2\\ &=\frac{1}{2}M \left(\frac{m+M}{m} \right)(v_M-v_{CM})^2\\ &=\frac{1}{2}M \left(\frac{m+M}{m} \right)\left(\frac{m}{m+M}(v_M-v_m)\right)^2\\ &=\frac{1}{2} \left(\frac{mM}{m+M}\right)(v_M-v_m)^2\end{aligned}\]

donde usamos nuestras expresiones anteriores para simplificar la expresión. Cuando el resorte se comprime al máximo, los dos bloques están en reposo y la energía mecánica del sistema,\(E'\), se “almacena” como energía potencial de resorte:\[\begin{aligned} E'&=\frac{1}{2}kx^2\end{aligned}\] donde\(x\) está la distancia a la que se comprime el resorte. Equiparar los dos nos permite determinar la compresión máxima del resorte:\[\begin{aligned} E &= E' \\ \frac{1}{2} \left(\frac{mM}{m+M}\right)(v_M-v_m)^2 &= \frac{1}{2}kx^2\\ \therefore x &= \sqrt{\frac{1}{k} \left(\frac{mM}{m+M}\right)}(v_M-v_m)\end{aligned}\]

Discusión:

Al modelar la colisión en el marco de referencia del centro de masa, pudimos determinar fácilmente la compresión máxima del resorte. Esto hubiera sido más difícil en el marco de referencia de laboratorio, ya que los dos bloques seguirían moviéndose cuando el resorte está comprimido al máximo, por lo que habríamos necesitado determinar sus velocidades para determinar la energía mecánica total cuando se comprime el resorte.

Cuando calculamos la energía cinética inicial, encontramos que estaba dada por:\[\begin{aligned} E=\frac{1}{2} \left(\frac{mM}{m+M}\right)(v_M-v_m)^2 &=\frac{1}{2}M_{red}(v_M-v_m)^2\end{aligned}\] La combinación de masas entre paréntesis se llama la “masa reducida” del sistema, y es una especie de masa efectiva que puede ser utilizada para modelar el sistema como un todo.

Ejercicio\(\PageIndex{3}\)

Un cable uniforme se dobla en un semicírculo de radio\(R\). Where is the center of mass of the wire?

Contestar

El alambre curvo se ilustra en la Figura\(\PageIndex{3}\), junto con un elemento de masa pequeña\(dm\),, en el alambre, y nuestra elección del sistema de coordenadas (centrado en el centro del semicírculo). Por simetría, la posición del centro de masa se ubicará en\(x=0\), por lo que solo necesitamos determinar la\(y\) posición.

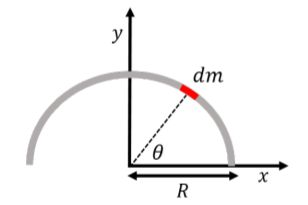
Figura\(\PageIndex{3}\): Un alambre uniforme doblado en un semicírculo de radio\(R\), y un elemento de masa pequeña,\(dm\), en el alambre.

La\(y\) posición del centro de masa viene dada por:\[\begin{aligned} y_{CM} = \frac{1}{M}\int y dm\end{aligned}\] donde\(M\) está la masa total del alambre. Podemos definir la masa por unidad de longitud,\(\lambda\), para el alambre como:\[\begin{aligned} \lambda =\frac{M}{\pi R}\end{aligned}\] Escogeremos integrar la ecuación para la\(y\) posición del centro de masa sobre\(\theta\) (de 0 a\(\pi\)), en lugar de sobre\(y\), como hará que la integral sea más fácil (es más fácil de expresar\(dm\) en términos de\(d\theta\) que\(dy\) porque el cable es curvo). \(\theta\)es el ángulo en el que se encuentra el elemento de masa. El elemento de masa forma un arco en el cable de longitud\(ds\) que subtiende un ángulo\(d\theta\). Los dos están relacionados por:\[\begin{aligned} ds = Rd\theta\end{aligned}\] El elemento de masa\(dm\),, puede entonces expresarse en términos de la masa por unidad de longitud del alambre y la longitud\(Rd\theta\),, del elemento de masa: También\[\begin{aligned} dm = \lambda ds = \lambda Rd\theta\end{aligned}\] necesitamos expresar la\(y\) posición del elemento de masa utilizando\(\theta\):\[\begin{aligned} y = R\sin\theta\end{aligned}\] Ahora que hemos expresado\(dm\) y\(y\) en términos de\(\theta\), podemos determinar la\(y\) posición del centro de masa:\[\begin{aligned} y_{CM} &= \frac{1}{M}\int y dm = \frac{1}{M}\int_0^\pi R\sin\theta \lambda Rd\theta\\ &= \frac{R^2\lambda}{M}\int_0^\pi \sin\theta d\theta = \frac{R^2\lambda}{M} \bigl[-\cos\theta\bigr]_0^\pi\\ &=\frac{2R^2\lambda}{M}=\frac{2R}{\pi}\end{aligned}\] donde en la última igualdad, usamos la expresión para la masa por unidad de longitud,\(\lambda\), obtenida anteriormente.