11.1: Vectores cinemáticos rotacionales

Antes de continuar, es posible que desee revisar:

revisar temas

• Sección 4.4 sobre cinemática para movimiento circular.
• Sección A1.3 sobre el producto vector.
• Sección A1.4 sobre vectores axiales y su uso en la definición de cantidades rotacionales.

Cantidades cinemáticas rotacionales escalares

Recordemos que podemos describir el movimiento de una partícula a lo largo de un círculo de radio\(R\),, usando su posición angular\(\theta\),, su velocidad angular\(\omega\), y su aceleración angular,\(\alpha\). Con una elección adecuada del sistema de coordenadas, la posición angular puede definirse como el ángulo formado por el vector de posición de las partículas\(\vec r\), y el\(x\) eje de un sistema de coordenadas cuyo origen es el centro del círculo, como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Posición angular para una partícula que se mueve alrededor del\(z\) eje (fuera de la página), a lo largo de un círculo de radio\(R\) con un centro en el origen.

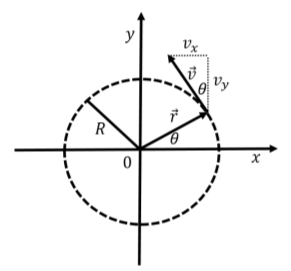
La velocidad angular,\(\omega\), es la velocidad del cambio de la posición angular, y la aceleración angular,\(\alpha\), es la velocidad de cambio de la velocidad angular:\[\begin{aligned} \omega &= \frac{d}{dt}\theta \\ \alpha &= \frac{d}{dt}\omega\end{aligned}\] Si la aceleración angular es constante, entonces la velocidad angular y la posición en función del tiempo son dado por:\[\begin{aligned} \omega(t) = \omega_0+\alpha t\\ \theta(t) = \theta_0+\omega_0 t+\frac{1}{2}\alpha t^2\end{aligned}\] donde\(\theta_0\) y\(\omega_0\) son la posición angular y la velocidad, respectivamente, at\(t=0\).

También podemos describir el movimiento de la partícula en términos de cantidades “lineales” (a diferencia de cantidades “angulares”) a lo largo de un eje unidimensional que se curva a lo largo del círculo. Si\(s\) es la distancia a lo largo de la circunferencia del círculo, medida en sentido antihorario desde donde el círculo se cruza con el\(x\) eje, entonces se relaciona con el desplazamiento angular:\[\begin{aligned} s = R\theta\end{aligned}\] si\(\theta\) se expresa en radianes. De igual manera, la velocidad lineal a lo largo del\(s\) eje\(v_s\), y la aceleración correspondiente\(a_s\),, están dadas por:\[\begin{aligned} v_s &= \frac{ds}{dt} =\frac{d}{dt}R\theta = R\omega\\ a_s&= \frac{dv}{dt} =\frac{d}{dt}R\omega = R\alpha\end{aligned}\] donde el radio del círculo,\(R\), es una constante que puede ser sacada de las derivadas del tiempo. Para el movimiento a lo largo de un círculo, el vector de velocidad\(\vec v\),, de la partícula es siempre tangente al círculo (Figura\(\PageIndex{1}\)), por lo que\(v_s\) corresponde a la velocidad de la partícula. El vector de aceleración\(\vec a\),, en general no es tangente al círculo;\(a_s\) representa el componente del vector de aceleración que es tangente al círculo. Si\(a_s=0\), entonces\(\alpha=0\), y la partícula se mueve con una velocidad constante (movimiento circular uniforme), y el vector de aceleración apunta hacia el centro del círculo.

Ejercicio\(\PageIndex{1}\)

¿Cuál de las siguientes afirmaciones describe correctamente las velocidades en los puntos\(A\) and \(B\) on the disk rotating about an axis through its center, as illustrated in Figure \(\PageIndex{2}\)?

Figura\(\PageIndex{2}\): Dos puntos en diferentes radios en un disco giratorio.

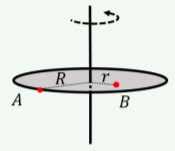
1. Ambos puntos\(A\) y\(B\) tienen las mismas velocidades angulares y lineales.
2. Ambos puntos\(A\) y\(B\) tienen la misma velocidad lineal pero tienen diferentes velocidades angulares.
3. Ambos puntos\(A\) y\(B\) tienen la misma velocidad angular pero tienen diferentes velocidades lineales.

Responder

Cantidades cinemáticas rotacionales vectoriales

En la sección anterior, definimos cantidades angulares para describir el movimiento de una partícula alrededor del\(z\) eje a lo largo de un círculo de radio\(R\) que se encuentra en el\(xy\) plano. Mediante el uso de vectores, podemos definir las cantidades angulares para la rotación alrededor de un eje que puede apuntar en cualquier dirección. Dado un eje de rotación, la trayectoria de cualquier partícula que gire alrededor de ese eje puede describirse mediante un círculo que se encuentra en el plano perpendicular a ese eje de rotación, como se ilustra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Definir el vector\(\vec r\) y la velocidad angular,\(\vec w\) para una partícula con velocidad que\(\vec v\) gira alrededor de un eje en una dirección general.

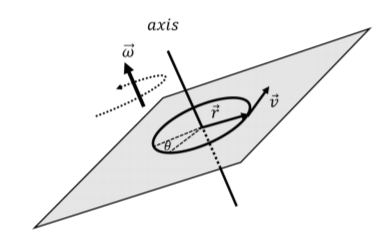
Definimos el vector,\(\vec r\), para que una partícula sea el vector que va desde el eje de rotación a la partícula y se encuentre en un plano perpendicular al eje de rotación, como en la Figura\(\PageIndex{3}\). Dado el vector de velocidad de la partícula,\(\vec v\), definimos su vector de velocidad angular\(\vec\omega\),, alrededor del eje de rotación, como:

\[\vec w=\frac{1}{r^{2}}\vec r\times \vec v\]

El vector de velocidad angular es perpendicular tanto al vector de velocidad como al vector\(\vec r\), ya que se define como su producto cruzado. Así, el vector de velocidad angular es colineal con el eje de rotación. Mediante el uso del vector de velocidad angular, podemos especificar la dirección del eje de rotación así como la dirección en la que la partícula está girando alrededor de ese eje. El sentido de rotación viene dado por la regla de la mano derecha para vectores axiales: cuando apuntas tu pulgar en la misma dirección que el vector de velocidad angular, la dirección de rotación es la dirección que apuntan tus dedos cuando los rizas, como se ilustra en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Uso de la regla de la derecha para vectores axiales. En este caso, la dirección de rotación es en sentido contrario a las agujas del reloj al mirar la página (la dirección en la que se rizan los dedos), por lo que el vector de rotación apunta fuera de la página (la dirección del pulgar).

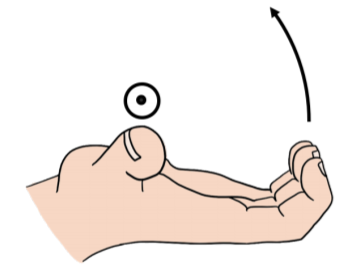
Esta definición de la velocidad angular es consistente con la descripción de la sección anterior para el movimiento alrededor de un círculo de radio\(R\) que se encuentra en el\(xy\) plano, como en la Figura\(\PageIndex{1}\). En ese caso, la magnitud de la velocidad angular viene dada por:\[\begin{aligned} \omega &=\frac{1}{r^2} || \vec r \times \vec v||= \frac{1}{r^2}r v\sin\phi= \frac{v}{R}\\ \therefore v &= R\omega\end{aligned}\] donde\(\phi\) está el ángulo entre los vectores\(\vec r\) y\(\vec v\) (\(90^{\circ}\)para el movimiento alrededor de un círculo). La dirección de la velocidad angular en la Figura\(\PageIndex{1}\) es en la\(z\) dirección positiva, que corresponde a la rotación en sentido contrario a las agujas del reloj alrededor del\(z\) eje.

Ejercicio\(\PageIndex{2}\)

Empujas en el lado derecho de una puerta para abrirla, ya que las bisagras de la puerta están a la izquierda. El vector de velocidad angular de la puerta es:

1. Hacia arriba
2. Hacia abajo
3. Adelante
4. Hacia atrás

Responder

Siempre se puede definir un vector de velocidad angular relativo a un punto de rotación, incluso si la partícula no se mueve a lo largo de un círculo. Si definimos el vector\(\vec r\) como el vector desde el punto de rotación a la partícula, entonces el vector de velocidad angular describe el movimiento de la partícula como si se estuviera moviendo instantáneamente en un círculo centrado en el punto de rotación, en un plano dado por los vectores \(\vec r\)y\(\vec v\).

Consideremos, por ejemplo, la partícula en la Figura\(\PageIndex{5}\) que se mueve en línea recta con un vector de velocidad en el\(xy\) plano en una posición\(\vec r\) relativa al origen. Podemos definir su vector de velocidad angular relativo al origen, que estará en la\(z\) dirección positiva.

Figura\(\PageIndex{5}\): Posición angular para una partícula que se mueve en línea recta.

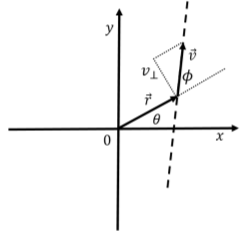
La velocidad angular describe el movimiento de la partícula como si se estuviera moviendo instantáneamente a lo largo de un círculo de radio\(r\) centrado alrededor del origen. La velocidad angular está relacionada con el componente de\(\vec v\),\(v_\perp\), que es perpendicular a\(\vec r\) (que es el componente tangente al círculo de radio\(r\), en la Figura\(\PageIndex{5}\)):

\[||\vec w || =\frac{1}{r^{2}}||\vec r\times \vec v || = \frac{v\sin φ}{r}=\frac{v\perp}{r}\]

donde\(\phi\) esta el angulo entre\(\vec r\) y\(\vec v\).

Del mismo modo, podemos definir el vector de aceleración angular,\(\vec \alpha\), alrededor de un eje de rotación:

\[\vec \alpha = \frac{1}{r^{2}}\vec r\times\vec a\]

donde\(\vec a\) es el vector de aceleración de la partícula, y\(\vec r\) es el vector desde el eje de rotación a la partícula. La dirección de la aceleración angular es colineal con el eje de rotación y la regla de la derecha da la dirección de rotación de la aceleración angular. También podemos definir la aceleración angular alrededor de un punto; en ese caso, la dirección del vector definirá un eje de rotación instantáneo alrededor de un círculo de radio\(r\) centrado en el punto así como la dirección de la aceleración angular alrededor de ese eje.

Finalmente, podemos definir un vector de desplazamiento angular,\(\vec \theta\), relativo a un eje de rotación. La dirección del vector de desplazamiento angular será colineal con el eje de rotación, su dirección indicará la dirección de rotación alrededor de ese eje, y su magnitud (en radianes) corresponderá al desplazamiento angular (como se muestra en la Figura\(\PageIndex{3}\)). Solo podemos relacionar el vector de desplazamiento angular con un vector de desplazamiento lineal infinitesimal\(d\vec s\), ya que el vector\(\vec r\) de posición desde el eje de rotación será diferente en cada extremo del vector de desplazamiento si el desplazamiento es grande. El vector de desplazamiento angular infinitesimal que corresponde a un vector de desplazamiento infinitesimal,\(d\vec s\), se define como:\[\begin{aligned} d\vec \theta &= \frac{1}{r^2} \vec r \times d\vec s\\\end{aligned}\]

Ejercicio\(\PageIndex{3}\)

¿Qué afirmación es correcta con respecto a una hormiga en un disco que está rotando cada vez más lentamente como se ilustra?

Figura\(\PageIndex{6}\): Una hormiga en un disco.

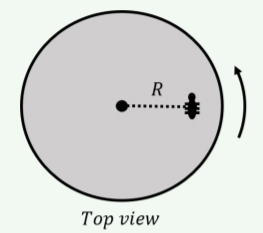
1. La velocidad angular apunta hacia la página y la aceleración angular apunta fuera de la página.
2. Tanto la velocidad angular como la aceleración apuntan a la página.
3. Tanto la velocidad angular como la aceleración apuntan fuera de la página.
4. La aceleración angular apunta hacia la página y la velocidad angular señala fuera de la página.

Responder

El vector de velocidad angular instantánea es la velocidad de cambio del vector de desplazamiento angular:\[\begin{aligned} \vec\omega &= \frac{d\vec \theta}{dt} = \frac{d}{dt} \frac{1}{r^2} \vec r \times d\vec s = \frac{1}{r^2} \vec r \times \vec v_s\end{aligned}\] donde\(\vec v_s\) está la velocidad tangencial (instantánea) alrededor del círculo (es decir, la componente de la velocidad\(\vec v\) que es perpendicular a\(\vec r\)). El vector de aceleración angular es la velocidad de cambio del vector de velocidad angular:\[\begin{aligned} \vec\alpha = \frac{d}{dt} \vec \omega\end{aligned}\]

Dadas las cantidades cinemáticas angulares, las cantidades lineales relacionadas en una posición\(\vec r\) desde el eje de rotación vienen dadas por:

\[d\vec s=d\vec\theta\times\vec r\]

\[\vec v_{s}=\vec w\times\vec r\]

\[\vec a_{s}=\vec\alpha\times\vec r\]

donde las cantidades lineales están siempre en la dirección perpendicular a\(\vec r\) (tangente al círculo, para el movimiento alrededor de un círculo). En otras palabras, no se puede, digamos, tomar el vector de aceleración, obtener el vector de aceleración angular, y luego recuperar el vector de aceleración original; uno solo recuperará el componente del vector de aceleración que es perpendicular al\(\vec r\).

Ejercicio\(\PageIndex{4}\)

Una partícula tiene una velocidad angular en negativo\(z\) direction. In which way is the particle’s velocity vector at a point in its trajectory when it is on the positive \(y\) axis?

1. \(z\)Dirección positiva
2. \(y\)Dirección negativa
3. \(x\)Dirección positiva
4. \(x\)Dirección negativa

Responder