11.2: Dinámica rotacional para una sola partícula

Supongamos que una sola fuerza\(\vec F\),, está actuando sobre una partícula de masa\(m\). La Segunda Ley de Newton para la partícula viene dada entonces por:\[\begin{aligned} \vec F = m \vec a\end{aligned}\] Podemos definir un punto de rotación tal que\(\vec r\) sea la posición de la partícula relativa a ese punto. Podemos tomar el producto cruzado de\(\vec r\) con ambos lados de la ecuación en la Segunda Ley de Newton:\[\begin{aligned} \vec r \times \vec F &= m \vec r \times \vec a\end{aligned}\]

El lado izquierdo de la ecuación se llama “el par de torsión\(\vec F\) relativo al punto de rotación”, y generalmente se denota por\(\vec \tau\):

\[\vec\tau = \vec r\times \vec F\]

El lado derecho de la ecuación está relacionado con el vector de aceleración angular,\(\vec \alpha\), sobre ese punto de rotación:\[\begin{aligned} m \vec r \times \vec a = mr^2\vec\alpha\end{aligned}\] Poniendo esto en conjunto, obtenemos:\[\begin{aligned} \vec\tau = mr^2 \vec\alpha\end{aligned}\]

Si se ejerce más de una fuerza sobre la partícula, es fácil demostrar que el par neto de la fuerza neta sobre la partícula es igual a la suma de los pares en la partícula:\[\begin{aligned} \vec r \times (\vec F_1 + \vec F_2 + \vec F_3 + \dots) &= (\vec r \times \vec F_1 + \vec r \times \vec F_2 + \vec r \times \vec F_3 + \dots) \\ \therefore \vec r \times \sum \vec F &= \sum \vec \tau = \vec \tau^{net}\end{aligned}\]

Podemos escribir “La Segunda Ley de Newton para la dinámica rotacional de una partícula”:

\[\sum \vec\tau = \vec\tau ^{net}=mr^{2}\vec\alpha\]

Esta ecuación nos proporciona una formulación alternativa a la Segunda Ley de Newton que es útil para describir el movimiento de una partícula que está rotando. El lado izquierdo de la ecuación corresponde a las “causas del movimiento” (al igual que la suma de las fuerzas en la Segunda Ley de Newton), y el lado derecho de la ecuación a la inercia y la cinemática. Algunas cosas a tener en cuenta al comparar con la Segunda Ley de Newton:

1. Las cantidades rotacionales, par y aceleración angular, solo se definen con respecto a un punto o eje de rotación (ya que esto determina el vector\(\vec r\)). Si uno elige un punto de rotación diferente, entonces el par y la aceleración angular serán diferentes.
2. La aceleración angular de una partícula es proporcional al par neto ejercido sobre ella, al igual que la aceleración lineal es proporcional a la fuerza neta ejercida sobre la partícula.
3. El par alrededor de un centro de rotación puede pensarse como el equivalente a una fuerza que hace que las cosas giren alrededor de un eje que pasa por el punto de rotación y que es paralelo a los vectores de par /aceleración angular.
4. En lugar de masa, son los tiempos de masa los\(r^2\) que desempeñan el papel de inercia y determinan qué tan grande de aceleración angular experimentará una partícula para un par neto dado.

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{1}\): Un cohete de juguete que acelera alrededor de un círculo de radio\(R\), visto desde arriba.

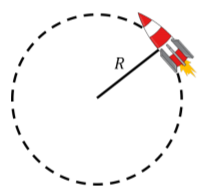
Un cohete de juguete está unido a una cuerda en una mesa horizontal sin fricción, como se muestra en la Figura\(\PageIndex{1}\). The rocket has a mass \(m\) and produces a constant force of thrust with a magnitude \(F\) that accelerates the rocket along a circle of radius \(R\) (the length of the string). If the rocket starts at rest, what distance along the circumference of the circle will the rocket have traveled after a time, \(t\)?

Solución:

Podemos modelar el cohete como una partícula puntual de masa\(m\) con las siguientes fuerzas ejercidas sobre él:

1. \(\vec F\), el empuje del cohete, actuando siempre tangente al círculo.
2. \(\vec T\), la fuerza de tensión en la cuerda, actuando siempre hacia el centro del círculo.
3. \(\vec F_g\), el peso del cohete, actuando en la página, con magnitud\(mg\).
4. \(\vec N\), una fuerza normal ejercida por la tabla, fuera de la página, con magnitud\(mg\).

Debido a que la fuerza normal y el peso son iguales en magnitud y opuestos en dirección, la fuerza neta será la suma de la fuerza de empuje y la fuerza de tensión, que siempre son perpendiculares entre sí. Pensando en esto con la Segunda Ley de Newton, podríamos modelar la fuerza de empuje como aumentando la velocidad de la partícula, mientras que la fuerza de tensión mantiene al cohete moviéndose en círculo (no puede hacer trabajo para aumentar la velocidad, ya que siempre es perpendicular al movimiento).

También podemos pensar en esto en términos de pares y aceleración angular alrededor del centro del círculo. El empuje dará como resultado un par neto alrededor del centro de rotación, lo que conducirá a que el cohete tenga una aceleración angular. Al determinar la aceleración angular, podemos entonces modelar el desplazamiento en algún momento,\(t\), utilizando la cinemática. La fuerza de tensión no creará ningún par alrededor del centro del círculo porque la fuerza de tensión siempre es colineal con el vector de posición,\(\vec r\) (el producto cruzado de los vectores colineales es siempre cero).

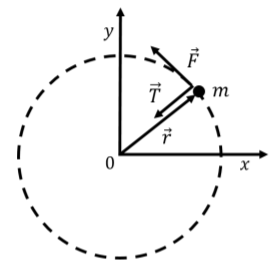
Introducimos un sistema de coordenadas cuyo origen coincide con el centro del círculo, como se muestra en la Figura\(\PageIndex{2}\), de manera que\(\vec r\) corresponde a la posición del cohete con relación al origen. La fuerza de empuje y la tensión también se muestran en el diagrama. Elegimos la dirección del\(x\) eje de tal manera que el cohete se ubicó en la intersección del\(x\) eje y el círculo en el momento,\(t=0\).

Figura\(\PageIndex{2}\): Sistema de coordenadas para describir el movimiento del cohete.

El par neto en el cohete alrededor del punto de rotación viene dado por el producto cruzado entre la fuerza de empuje,\(\vec F\), y el vector de posición,\(\vec r\):\[\begin{aligned} \vec\tau^{net} = \vec r\times\vec F\end{aligned}\] y apuntará en la\(z\) dirección positiva (según lo dado por la regla de la mano derecha). \(\vec r\)y\(\vec F\) son perpendiculares, por lo que la magnitud del par neto viene dada por:\[\begin{aligned} \tau^{net} = rF \sin(90^{\circ}) = RF\end{aligned}\] donde\(R\) esta la magnitud de\(\vec r\). El vector de par neto es así:\[\begin{aligned} \vec\tau^{net} = RF \hat z\end{aligned}\] Aplicar la versión rotacional de la Segunda Ley de Newton nos permite determinar la aceleración angular:\[\begin{aligned} \vec \tau ^{net} &= mr^2\vec\alpha\\ RF \hat z&= mR^2\vec\alpha\\ \therefore \vec \alpha &= \frac{F}{mR}\hat z\end{aligned}\] El vector de aceleración angular apunta en la\(z\) dirección positiva (al igual que el par neto), e indica que el cohete está acelerando en sentido contrario a las agujas del reloj alrededor del\(z\) eje.

Después de un periodo de tiempo\(t\), el cohete habrá cubierto un desplazamiento angular\(\Delta \theta\),, dado por:\[\begin{aligned} \Delta \theta &= \theta(t)-\theta_0 = \omega_0t + \frac{1}{2}\alpha t^2\\ &=\frac{1}{2}\frac{F}{mR} t^2\end{aligned}\] El desplazamiento lineal,\(\Delta s\), que corresponde a este desplazamiento angular es:\[\begin{aligned} \Delta s = R \Delta\theta = \frac{1}{2}\frac{F}{m} t^2\end{aligned}\]

Discusión:

La fórmula que encontramos para el desplazamiento lineal total es la misma que habríamos encontrado si la partícula se estuviera moviendo en línea recta con una fuerza neta\(F\) aplicada a ella (ya que la partícula tendría una aceleración constante dada por\(F/m\)).