11.4: Rotación alrededor de un eje versus rotación alrededor de un punto.

Al definir cantidades angulares (torque, aceleración angular, etc.), es importante identificar si estas se definen con relación a un eje o a un punto de rotación. Esto, a su vez, determina el vector\(\vec r\) que está involucrado en la definición de las cantidades angulares.

Considera un disco de radio\(r\) con una fuerza,\(\vec F\) ejercida sobre su perímetro, como se ilustra en la Figura\(\PageIndex{1}\). El disco sólo puede girar alrededor de un eje que es perpendicular al disco y que pasa por el centro del disco, como una rueda montada en un eje. La fuerza tiene un componente,\(\vec F_{plane}\), que se encuentra en el plano perpendicular al eje de rotación, y un componente,\(\vec F_{axis}\), que es paralelo al eje de rotación.

Figura\(\PageIndex{1}\): Una fuerza ejercida sobre el disco que solo puede girar alrededor de un eje a través de su centro y perpendicular a su plano. Solo el componente de\(\vec F\) eso está en el plano perpendicular al eje de rotación,\(\vec F\) plano, contribuirá al par alrededor del eje de rotación.

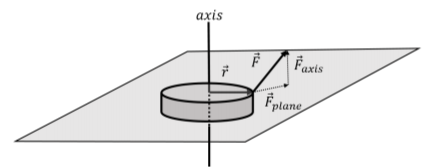
El vector siempre\(\vec r\) se define para ser perpendicular al eje de rotación y para ir desde el eje de rotación al punto donde \(\vec F\)se ejerce la fuerza, como se ilustra. El par obtenido al tomar el producto cruzado:\[\begin{aligned} \vec \tau = \vec r \times \vec F\end{aligned}\] será perpendicular a ambos\(\vec r\) y\(\vec F\), y por lo tanto no será paralelo al eje de rotación. Solo el componente del par que es paralelo al eje de rotación contribuirá a rotar el disco alrededor del eje. Sólo la componente de la fuerza que se encuentra en el plano perpendicular al eje de rotación\(\vec F_{plane}\),, contribuirá a la componente del par alrededor de ese eje de rotación. Así, cuando necesitamos determinar el par alrededor de un eje de rotación, podemos considerar vectores\(\vec r\) y \(\vec F\)que se encuentran en el plano perpendicular al eje de rotación. El par de torsión\(\vec F\) relativo al eje de rotación es así:\[\begin{aligned} \vec \tau_{axis} = \vec r \times \vec F_{plane}\end{aligned}\] Además, sólo el componente de\(\vec F_{plane}\) que es perpendicular a\(\vec r\) contribuirá a ese par, como vimos en la sección anterior.

En general, los objetos sólidos como un disco solo pueden rotar alrededor de un eje. En ese caso, solo se pueden considerar los componentes de las fuerzas que se encuentran en el plano perpendicular al eje de rotación para calcular los componentes de los pares alrededor de ese eje que son paralelos a ese eje.

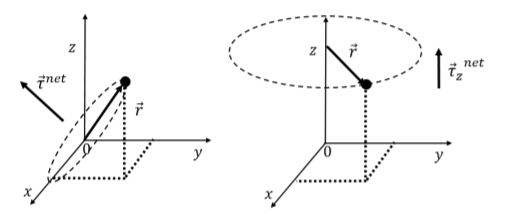
Una partícula puntual puede ser capaz de rotar alrededor de cualquier eje que pase por un punto de rotación. El vector de par neto en la partícula alrededor de ese punto indicará la dirección del eje alrededor del cual giraría la partícula. Esto se ilustra en el panel izquierdo de la Figura\(\PageIndex{2}\).

En cambio, si la partícula estuviera restringida a girar alrededor del\(z\) eje (por ejemplo, si la partícula está en una pista), entonces usaríamos el componente del vector de par que es paralelo al\(z\) eje para describir su movimiento, como se ilustra en el panel derecho. El\(z\) componente del par podría determinarse utilizando solo los componentes de las fuerzas que se encuentran en el plano perpendicular al eje, y definiendo el vector\(\vec r\) desde el eje a la partícula en lugar de desde el punto de rotación a la partícula.

Figura\(\PageIndex{2}\): Panel izquierdo: una partícula que gira alrededor de un círculo centrado en el origen con un eje determinado a partir del vector de par neto. Panel derecho: una partícula que está restringida a girar alrededor del\(z\) eje.

Ejemplo\(\PageIndex{1}\)

Una fuerza dada por\(\vec F=F_x\hat x + F_y \hat y + F_z \hat z\) is exerted at a position \(\vec r=r_x \hat x + r_y \hat y + r_z\hat z\). Calculate the torque about the \(z\) axis as well as the torque about the origin.

Solución:

Para calcular el par alrededor del\(z\) eje, necesitamos tomar el producto cruzado entre los componentes de los vectores\(\vec r\) y\(\vec F\) que se encuentran en el\(x-y\) plano, ya que ese es el plano perpendicular al eje de rotación (el \(z\)eje). Esto da:\[\begin{aligned} \vec\tau_z =(r_x \hat x + r_y \hat y) \times (F_x\hat x + F_y \hat y) =(r_xF_y-r_yF_y)\hat z\end{aligned}\] Si en cambio queremos calcular el par sobre el origen, tomamos el producto cruzado entre los dos vectores:\[\begin{aligned} \vec\tau &=(r_x \hat x + r_y \hat y+ r_z\hat z) \times (F_x\hat x + F_y \hat y+ F_z \hat z)\\ &=(r_yF_z-r_zF_y)\hat x+(r_zF_x-r_xF_z)\hat y+(r_xF_y-r_yF_y)\hat z\end{aligned}\] Si una partícula se ubicara en la posición dada, la fuerza provocaría que la partícula gire (instantáneamente) alrededor de un eje que pasa por el origen y es paralelo al vector de par.

Discusión:

Este ejemplo destaca la diferencia entre calcular el par alrededor de un eje de rotación y determinar el par alrededor de un punto. Al calcular el par alrededor de un eje que pasa por el origen, solo consideramos los componentes de los vectores\(\vec r\) y\(\vec F\) que están en el plano perpendicular al eje de rotación. Esto correspondería a una situación en la que la partícula está restringida a moverse en un plano que es perpendicular al eje de rotación. En cambio, si calculamos el par sobre el origen, entonces el vector de par determina el eje de rotación a través del origen alrededor del cual giraría la partícula. En este caso, dado que el eje de rotación es el\(z\) eje, y el punto de rotación fue el origen, el par alrededor\(z\) del eje fue simplemente el\(z\) componente del par calculado alrededor del origen.