11.5: Dinámica rotacional para un objeto sólido

Ahora consideramos la dinámica rotacional de un objeto sólido alrededor de un eje de rotación específico. Al igual que hicimos en el Capítulo 10, modelamos un objeto sólido como un sistema hecho de muchas partículas de masa\(m_i\). Debido a que todos los puntos de un sólido deben moverse al unísono, todos giran alrededor de un eje de rotación en lugar de un punto. Describimos la posición de cada partícula\(i\) mediante un vector\(\vec r_i\) que es perpendicular al eje de rotación y va desde el eje a la partícula correspondiente, como se muestra en la Figura 11.5.1.

Figura\(\PageIndex{1}\): Dos partículas puntuales que forman parte de un objeto sólido grande y sus vectores de posición con respecto a un eje de rotación.

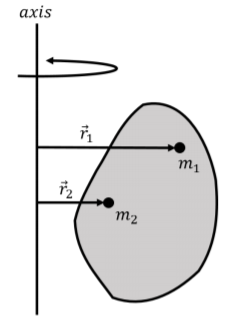
Deseamos modelar el movimiento del objeto a medida que gira alrededor de un eje específico. Así, al considerar el par neto en cualquier partícula\(i\), solo consideramos el componente del par neto de la partícula que es paralelo al eje de rotación (ese componente del par que proviene de fuerzas que están en el plano perpendicular al eje de rotación).

Podemos escribir la versión rotacional de la Segunda Ley de Newton para la partícula\(i\), con el vector de masa\(m_i\) y posición\(\vec r_i\) relativo al eje de rotación:\[\begin{aligned} \sum_k \vec\tau_{ik} = \vec\tau_i^{net} &= m_ir_i^2\vec\alpha_i\end{aligned}\] donde\(\vec\tau_{ik}\) está el\(k\) -ésimo par sobre la partícula \(i\). \(\vec\tau_i^{net}\)es el par neto en la partícula alrededor del eje de rotación y\(\vec\alpha_i\) es la aceleración angular de la partícula alrededor de ese eje.

Podemos dividir los pares ejercidos sobre una partícula en pares internos y externos. Los pares internos son los que ejerce otra partícula en el sistema, mientras que los pares externos son ejercidos por algo externo al sistema. Si la partícula 1 ejerce un par\(\vec\tau\) sobre la partícula 2, la partícula 2 ejercerá un par igual y opuesto,\(-\vec\tau\) sobre la partícula 1.

En efecto, consideremos las dos partículas que ejercen una fuerza igual y opuesta (la Tercera Ley de Newton),\(\vec F\), una sobre la otra, y un punto/eje de rotación arbitrario, como se ilustra en la Figura\(\PageIndex{2}\). El par sobre la partícula 1 a partir de la fuerza ejercida por la partícula 2 tendrá la misma magnitud que el par sobre la partícula 2 de la fuerza por partícula 1. Esto se debe a que ambas fuerzas tienen la misma magnitud y son colineales, lo que da como resultado que tengan el mismo brazo de palanca. El vector de par de cada fuerza estará en direcciones opuestas, ya que las fuerzas están en dirección opuesta. Por lo tanto, la Tercera Ley de Newton también se sostiene para los pares.

Figura\(\PageIndex{2}\): Dos partículas ejercerán pares iguales y opuestos entre sí debido a la Tercera Ley de Newton; las fuerzas ejercidas por cada partícula sobre la otra son colineales y así tendrán el mismo brazo de palanca con relación a cualquier punto/eje de rotación.

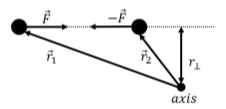
Podemos sumar juntas las ecuaciones para cada partícula\(i\):\[\begin{aligned} \vec\tau_1^{net} + \vec\tau_2^{net} +\vec\tau_3^{net} + \dots &= m_1r_1^2\vec\alpha_1 + m_2r_2^2\vec\alpha_2 +m_3r_3^2\vec\alpha_3 +\dots\\ \sum_i \vec\tau_i^{net} &= \sum_i m_ir_i^2\vec\alpha_i\end{aligned}\] donde la suma sobre todos los pares ejercidos sobre cada partícula será igual al par externo neto ejercido sobre todas las partículas, ya que la suma de los pares internos\(\vec\tau_i^{int}\),, será cero: \[\begin{aligned} \sum_i \vec\tau_i^{net} = \sum_i \vec\tau_i^{int} + \sum_i \vec\tau_i^{ext} = \sum_i \vec\tau_i^{ext} = \vec\tau^{ext}\end{aligned}\]donde\(\vec\tau^{ext}\) está el par externo neto en el sistema.

Todas las partículas son parte del mismo cuerpo rígido, y no pueden moverse una con relación a la otra. Además, todos deben moverse alrededor de círculos que están centrados alrededor del eje de rotación y en un plano perpendicular a ese eje. Por lo tanto, todos deben tener la misma aceleración angular ¹,\(\vec\alpha_i = \vec \alpha_1 = \vec \alpha_2 =\dots=\vec\alpha\). Podemos así factorizar la aceleración angular,\(\vec \alpha\), fuera de la suma.

Podemos escribir así la Segunda Ley de Newton para la dinámica rotacional de un objeto sólido como:

\[\begin{aligned} \sum_i \vec\tau_i^{net} &= \sum_i m_ir_i^2\vec\alpha_i\\ \therefore \vec\tau^{ext}&= \left(\sum_i m_ir_i^2\right)\vec\alpha\end{aligned}\]

El término entre paréntesis describe cómo se distribuyen las diversas masas en relación con el eje de rotación. El término entre paréntesis se llama el momento de inercia del objeto, y generalmente se denota con la letra,\(I\):

\[I=\sum_{i}m_{i}r_{i}^{2}\]

El momento de inercia es una propiedad del objeto en relación con un eje de rotación específico. Reescribir la Segunda Ley de Newton para la dinámica rotacional de objetos sólidos utilizando el momento de inercia:

\[\vec\tau ^{ext}=I\vec\alpha\]

El par neto ejercido sobre un objeto en la dirección del eje de rotación es así igual a su momento de inercia alrededor de ese eje multiplicado por su aceleración angular alrededor de ese eje. En otras palabras, el momento de inercia describe cómo el objeto resistirá el movimiento rotacional dado un par neto. Un objeto con un menor momento de inercia tendrá una aceleración angular mayor para un par dado. Nuevamente, esto es análogo al caso lineal, donde la aceleración de un objeto dada una fuerza neta viene determinada por su masa inercial.

Ejemplo\(\PageIndex{1}\)

Figura\(\PageIndex{3}\): Mancuerna compuesta por dos pequeñas masas idénticas separadas por una distancia\(L\).

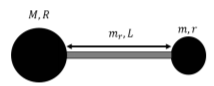
Dos pequeñas masas puntuales,\(m\), están conectadas por una varilla de longitud sin masa\(L\) para formar una mancuerna, como se ilustra en la Figura\(\PageIndex{3}\). \(F\)Se ejerce una fuerza neta de magnitud sobre cada masa, en direcciones opuestas, como se ilustra en la Figura.

1. ¿Cuál es la aceleración lineal del centro de masa de la mancuerna?
2. ¿Cuál es la aceleración angular de la mancuerna con relación a un eje que atraviesa su centro de masa y es perpendicular a la página?
3. ¿Cuál es la aceleración angular de la mancuerna con relación a un eje que atraviesa una de las masas y es perpendicular a la página?

Solución:

Modelamos la mancuerna como un cuerpo rígido compuesto por dos masas puntuales sostenidas a una distancia fija.

a. La aceleración lineal del centro de masa debe ser cero, porque la fuerza neta sobre la mancuerna es cero. No obstante, el hecho de que el centro de masa no se mueva no significa que todas las partes de la mancuerna estén inmóviles.

b. primero, calculamos la aceleración angular relativa a un eje que es perpendicular a la página y pasa por el centro de masa. El centro de masa se ubica a medio camino entre las dos masas, como se ilustra en la Figura\(\PageIndex{4}\). También definimos un sistema de coordenadas como se muestra, de tal manera que el\(z\) eje está fuera de la página.

Figura\(\PageIndex{4}\): La mancuerna que gira alrededor del centro de masa.

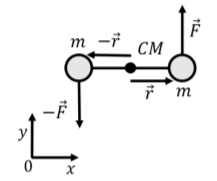
El vector desde el eje de rotación a cada masa tendrá la misma magnitud\(r\), pero diferentes direcciones. El par externo neto en la mancuerna relativo al eje que pasa por el centro de masa\(\vec\tau^{ext}\),, que es igual a la suma de los pares de cada fuerza:\[\begin{aligned} \vec\tau^{ext}&= \vec r \times \vec F + (-\vec r) \times (-\vec F) \\ &= 2 (\vec r \times \vec F)=2 (r\hat x \times F\hat y) = 2rF (\hat x \times \hat y)=2rF\hat z\\ &=LF\hat z\end{aligned}\] donde utilizamos el hecho de que\(2r = L\). El par neto es así distinto de cero y en la\(z\) dirección positiva; la mancuerna tendrá una aceleración angular que es paralela al par neto, y así acelerará en sentido contrario a las agujas del reloj.

El momento de inercia de la mancuerna con relación al eje a través del centro de masa viene dado por:\[\begin{aligned} I = \sum_i m_ir_i^2 = mr^2 +mr^2 = 2mr^2 = \frac{1}{2}mL^2\end{aligned}\] Usando la Segunda Ley de Newton para la dinámica rotacional, encontramos que la aceleración angular es:\[\begin{aligned} \vec\tau^{ext}&= I\vec\alpha\\ LF\hat z&=\frac{1}{2}mL^2\vec\alpha\\ \therefore \vec\alpha &= \frac{2F}{mL}\hat z\end{aligned}\] Debido a que el centro de masa es fijo (la suma de las fuerzas es cero), los dos extremos de la mancuerna girará alrededor de un eje que atraviesa el centro de masa. Esta es una característica de todas las situaciones en las que la fuerza neta sobre un objeto es cero y el par neto alrededor de un eje que atraviesa el centro de masa es distinto de cero.

c. Ahora calculemos la aceleración angular de la mancuerna alrededor de un eje que atraviesa una de las masas, como se ilustra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): La mancuerna girando alrededor de uno de sus extremos.

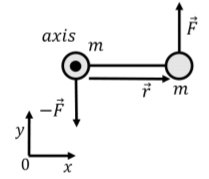
Primero calculamos el par neto en la mancuerna. El vector que va desde el eje de rotación a la fuerza ejercida sobre la masa que coincide con el eje de rotación es cero. Así, sólo la fuerza ejercida sobre la masa que no está en el eje de rotación contribuye al par neto:\[\begin{aligned} \vec\tau^{ext}&= \vec r \times \vec F = LF\hat z\end{aligned}\] El momento de inercia de la mancuerna alrededor de este eje es:\[\begin{aligned} I = \sum_i m_ir_i^2 = m(0)^2 + m(r^2) = mL^2\end{aligned}\] que es mayor de lo que era alrededor del centro de masa. Nuevamente, la aceleración angular se encuentra usando la Segunda Ley de Newton para la dinámica rotacional:\[\begin{aligned} \vec\tau^{ext}&= I\vec\alpha\\ LF\hat z&=mL^2\vec\alpha\\ \therefore \vec\alpha &= \frac{F}{mL}\hat z\end{aligned}\] Encontramos que la aceleración angular es más pequeña alrededor de un eje que atraviesa uno de la masa que alrededor de un eje a través del centro de masa. Debido a que el centro de masa de la mancuerna está fijo, sólo podemos pensar en la mancuerna como que gira instantáneamente alrededor de uno de sus extremos; es decir, el movimiento de la mancuerna no será tal que una masa gire alrededor de la otra; esto sólo es cierto instantáneamente.

Discusión:

Este sencillo ejemplo ilustra varias características clave sobre la dinámica rotacional:

• Si la suma de las fuerzas sobre un objeto es cero, no significa que todo el objeto sea estacionario; solo implica que el centro de masa es estacionario (o mejor dicho, moviéndose con una velocidad constante, pero siempre podemos elegir modelar el sistema en un marco de referencia donde el centro de masa es estacionario).
• Si la suma de las fuerzas sobre un objeto es cero, y la suma de los pares externos no es cero, el objeto girará alrededor de un eje que atraviesa el centro de masa. Es decir, todos los puntos del objeto se moverán a lo largo de círculos que están centrados en un eje que pasa por el centro de masa.
• Podemos modelar el objeto giratorio alrededor de cualquier eje que escojamos. En general, el par externo neto y el momento de inercia dependerán de la elección del eje, al igual que la aceleración angular resultante.
• Al determinar el movimiento del centro de masa, podemos dibujar un diagrama de cuerpo libre, y la ubicación de donde se ejercen las fuerzas no importa.
• Al determinar cómo gira el objeto, no podemos usar un diagrama de cuerpo libre, porque importa dónde se aplican las fuerzas (ya que el par de una fuerza dada depende de la ubicación donde se aplique la fuerza con relación al eje de rotación).

Notas al pie

1. Tendrán diferentes aceleraciones lineales, pero la aceleración angular (y velocidad angular) será la misma para todas las partículas si se mueven al unísono.