12.3: Momentum Angular

En esta sección, mostramos que podemos definir una cantidad llamada “momento angular” como el equivalente rotacional del momento lineal.

Momento Angular de una Partícula

El momento angular relativo a un punto de rotación,\(\vec L\), de una partícula con impulso lineal\(\vec p\), se define como:

\[\vec L = \vec r\times \vec p\]

donde\(\vec r\) es el vector desde el punto de rotación a la partícula, y el momento lineal,\(\vec p\), se define con relación a un marco inercial de referencia en el que el punto de rotación está en reposo.

Considere la derivada de tiempo del momento angular (donde tenemos que usar la regla del producto para las derivadas):

\[\begin{aligned} \frac{d\vec L}{dt} &= \frac{d}{dt} (\vec r\times \vec p)\\ &=\frac{d\vec r}{dt}\times \vec p + \vec r\times\frac{d\vec p}{dt}\\ &=\vec v\times \vec p + \vec r\times\frac{d\vec p}{dt}\\\end{aligned}\]

El primer término es cero, ya que\(\vec v\) es paralelo a\(\vec p\) por definición. Recordemos la Segunda Ley de Newton escrita usando impulso lineal:

\[\begin{aligned} \frac{d\vec p}{dt} = \vec F^{net}\end{aligned}\]

donde\(\vec F^{net}\) es la fuerza neta sobre la partícula en relación con el punto de rotación. Por lo tanto, la tasa de cambio del momento angular viene dada por:

\[\begin{aligned} \frac{d\vec L }{dt} &= \vec r\times\frac{d\vec p}{dt}\\ &=\vec r\times\vec F^{net}\end{aligned}\]

donde el término a la derecha es el par neto en la partícula. Así, la tasa de cambio del momento angular viene dada por:

\[\frac{d\vec L}{dt}=\vec\tau ^{net}\]

que es análogo al caso lineal, pero utilizamos momento angular en lugar de momento lineal y par neto en lugar de fuerza neta. El par neto en una partícula es así igual a la velocidad de cambio de su momento angular. En particular, el momento angular de una partícula permanecerá constante (no cambiará con el tiempo) si el par neto sobre la partícula es cero.

También podemos definir el momento angular de una partícula usando solo cantidades angulares:

\[\begin{aligned} \vec L = \vec r \times \vec p = m \vec r \times \vec v = mr^2 \vec\omega\end{aligned}\]donde factorizamos la masa\(m\) fuera del impulso y usamos la definición\(\vec \omega = 1/r^2(\vec r \times \vec v)\). Podemos pensar en\(mr^2\) el momento de inercia,\(I\), de la partícula y escribir:

\[\vec L = mr^{2}\vec\omega = I\vec\omega\]

que es un análogo cercano a la definición de momento lineal, pero usamos momento de inercia en lugar de masa y velocidad angular en lugar de velocidad.

El momento angular es así paralelo a la velocidad angular de la partícula alrededor del punto de rotación. Si no se ejerce un par neto sobre la partícula alrededor de ese punto, entonces el momento angular de la partícula alrededor de ese punto permanecerá constante. También podemos considerar el par y el momento angular alrededor de un eje en lugar de un punto; en ese caso, simplemente tomaríamos los componentes de par y momento angular que son paralelos a ese eje.

Ejemplo\(\PageIndex{1}\)

Un pequeño bloque de masa\(m\) unido a una cuerda sin masa se mueve a lo largo de un círculo de radio\(R\) sobre una mesa horizontal, como se representa desde arriba en la Figura\(\PageIndex{1}\). Si la tabla es sin fricción: ¿se conserva el momento lineal y/o angular del bloque con respecto al eje de rotación? Si hay fricción entre la mesa y el bloque, ¿se conserva el momento lineal y/o angular del bloque con respecto al eje de rotación? ¿Qué se puede decir de la energía cinética del bloque en los dos casos?

Figura\(\PageIndex{1}\): Un pequeño bloque unido a una cuerda sin masa que se mueve en círculo horizontal sobre una mesa.

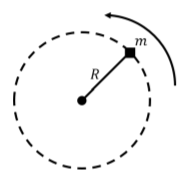
Solución:

Si no hay fricción entre el bloque y la mesa, entonces las fuerzas ejercidas sobre el bloque son:

1. \(\vec F_g\), el peso del bloque, ejercido hacia abajo, con magnitud\(mg\).
2. \(\vec N\), una fuerza normal, ejercida hacia arriba, con magnitud\(mg\).
3. \(\vec T\), una fuerza de tensión, ejercida hacia el centro del círculo.

Todas estas fuerzas son perpendiculares al desplazamiento (tangencial) del bloque a lo largo del círculo. Así, no se puede realizar ningún trabajo sobre el bloque y su velocidad,\(v\), debe permanecer constante. Por lo tanto, la energía cinética del bloque debe permanecer constante.

La suma de las fuerzas sobre el bloque debe ser hacia el centro del círculo, ya que el bloque está en movimiento circular uniforme. El momento lineal del bloque no se puede conservar si hay una fuerza neta sobre el bloque (y claramente, el vector de velocidad del bloque cambia de dirección a medida que va alrededor del círculo).

Las fuerzas de peso y la fuerza normal están ambas fuera del plano de movimiento y, por lo tanto, no pueden ejercer un par a lo largo del eje de rotación. También son iguales y opuestos en magnitud por lo que el par neto de esas dos fuerzas es siempre cero (ya que la fuerza neta de esas fuerzas es cero). La fuerza de tensión siempre es antiparalela al vector\(\vec r\), desde el eje de rotación hasta la partícula, y no puede dar como resultado un par alrededor del eje de rotación. Así, el par neto en el bloque es cero y su momento angular debe conservarse.

Si hay fricción cinética ejercida por la mesa sobre el bloque, entonces hay una fuerza adicional,\(\vec f_s\), ejercida sobre el bloque en la dirección opuesta al movimiento (tangente al círculo, en la dirección opuesta a la velocidad del bloque).

La fuerza de fricción hará un trabajo negativo sobre el bloque, ralentizándolo y reduciendo su energía cinética, que ya no se conserva. La fuerza neta sobre el bloque es diferente de cero, por lo que su impulso lineal aún no se conserva. Finalmente, la fuerza de fricción, que siempre es perpendicular a\(\vec r\), dará como resultado un par que reduce la velocidad angular del bloque. El momento angular del bloque ya no se conserva cuando hay fricción entre la mesa y el bloque.

Discusión

En este ejemplo, vimos que la energía cinética, el momento lineal y el momento angular se conservan bajo diferentes condiciones. La energía cinética se conserva si no se realiza ningún trabajo neto en el bloque. El momento lineal se conserva si la fuerza neta sobre el bloque es cero. El momento angular se conserva si el par neto en el bloque es cero. Al introducir el momento angular, podemos utilizar una nueva cantidad conservada para ayudarnos a modelar la dinámica rotacional.

Ejemplo\(\PageIndex{2}\)

Una partícula se mueve a velocidad constante\(\vec v\) (in a straight line) relative to a coordinate system in an inertial frame of reference, as shown in Figure \(\PageIndex{2}\). Show that its angular momentum about the origin is conserved.

Figura\(\PageIndex{2}\): Una partícula que se mueve en línea recta.

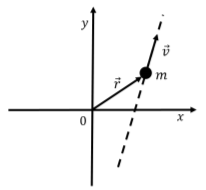
Solución:

En este caso, la partícula se mueve en línea recta, pero aún podemos definir su momento angular relativo al origen. Si\(\vec r\) es el vector de posición de la partícula en relación con el origen, su momento angular es:

\[\begin{aligned} \vec L = \vec r \times \vec p\end{aligned}\]

Podemos tomarnos el tiempo derivado del momento angular para ver si cambia con el tiempo:

\[\begin{aligned} \frac{d\vec L}{dt} = &= \frac{d}{dt} (\vec r\times \vec p)\\ &=\frac{d\vec r}{dt}\times \vec p + \vec r\times\frac{d\vec p}{dt}\\ &=\vec v\times \vec p + \vec r\times\frac{d\vec p}{dt}\\\end{aligned}\]

El primer término es cero porque\(\vec v\) y\(\vec p\) son paralelos (por lo que su producto cruzado debe ser cero). El segundo término es cero porque el momento de la partícula es constante en el tiempo (ya que su velocidad es constante). Así, el momento angular de la partícula no cambia con el tiempo, y se conserva.

Discusión:

Por supuesto, esperábamos este resultado ya que no se ejerce un par neto sobre la partícula. Sin embargo, cabe destacar que una partícula no necesita estar rotando para que su momento angular alrededor de un eje dado sea definida o conservada; lo único que importa es que no haya un par neto en la partícula con relación a ese eje.

Momento angular de un objeto o sistema

Considere un sistema hecho de muchas partículas de masa\(m_i\), cada una con una posición\(\vec r_i\), y velocidad,\(\vec v_i\), en relación con un punto de rotación que se fija en un marco inercial de referencia.

Podemos escribir la Segunda Ley de Newton usando el momento angular,\(\vec L_i\), para partícula\(i\):\[\begin{aligned} \frac{d\vec L_i}{dt} = \vec \tau_i^{net}\end{aligned}\] dónde\(\vec \tau_i^{net}\) está el par neto ejercido sobre la partícula\(i\). Podemos sumar cada lado de esta ecuación para todas las partículas en el sistema:\[\begin{aligned} \frac{d\vec L_1}{dt} + \frac{d\vec L_2}{dt} + \frac{d\vec L_3}{dt} + \dots &= \vec \tau_1^{net} + \vec \tau_2^{net} +\vec \tau_3^{net} + \dots\\ \therefore \frac{d}{dt} \sum_i\vec L_i &= \sum_i \vec \tau_i^{net}\end{aligned}\] La suma de todos los pares de torsión en todas las partículas incluirá una suma sobre pares que son internos al sistema y pares que son externos al sistema. La suma sobre los pares internos es cero:\[\begin{aligned} \sum_i \vec\tau_i^{net} = \sum_i \vec\tau_i^{int} + \sum_i \vec\tau_i^{ext} = \sum_i \vec\tau_i^{ext} = \vec\tau^{ext}\end{aligned}\] donde definimos,\(\vec\tau^{ext}\), para ser el par externo neto ejercido sobre el sistema. También introducimos el momento angular total del sistema,\(\vec L\), como la suma de los momentos angulares de las partículas individuales:\[\begin{aligned} \vec L = \sum_i\vec L_i\end{aligned}\] La tasa de cambio del momento angular total del sistema viene dada entonces por:

\[\frac{d\vec L}{dt}=\vec\tau^{ext}\]

Hasta este punto, no requeríamos que el sistema fuera un objeto sólido, por lo que las partículas en el sistema pueden moverse unas con respecto a otras. Por ejemplo, las partículas podrían ser el Sol, los planetas, y todo lo demás que esté en nuestro Sistema Solar. El momento angular total de todos los cuerpos en el Sistema Solar (digamos, relativo al Sol) se conserva si no hay un par neto en el sistema solar relativo al Sol (es decir, si no hay par alrededor del Sol ejercido sobre alguno de los cuerpos en el sistema que no es ejercido por uno de los otros cuerpos en el sistema).

Ahora, consideremos un objeto sólido que se modela como un sistema de muchas partículas de masa,\(m_i\), en posición,\(\vec r_i\), con velocidad,\(\vec v_i\), con relación a un eje fijo de rotación. Podemos definir el momento angular de una sola partícula como (Ecuación 12.3.3):\[\begin{aligned} \vec L_i = m_i r_i^2 \vec \omega_i^2\end{aligned}\] El momento total del sistema es la suma de los momentos angulares de las partículas individuales:\[\begin{aligned} \vec L &= \sum_i\vec L_i = \sum_i m_i r_i^2 \vec \omega_i^2\end{aligned}\] Debido a que todas las partículas son parte del mismo objeto, todas deben moverse al unísono y tener la misma velocidad angular,\(\vec\omega\), relativa al eje de rotación. Podemos definir así el momento angular alrededor del eje de rotación para un objeto sólido con velocidad angular\(\vec\omega\), como:

\[\vec L = \left(\sum_{i} m_{i}r_{i}^{2} \right) \vec\omega = I\vec\omega\]

donde reconocimos que la suma entre paréntesis es simplemente el momento de inercia del objeto relativo al eje de rotación. Nuevamente, hay que enfatizar que este es el momento angular total del objeto alrededor de un eje de rotación, y no alrededor de un punto.

Visualizar el par y el momento angular de un sistema puede ser un desafío porque casi siempre requiere visualizar algo en tres dimensiones. Considere una rueda (por ejemplo, una rueda de bicicleta) que esté girando alrededor del eje horizontal que sostiene con las manos, como se ilustra en el panel izquierdo de la Figura\(\PageIndex{3}\) (sin las manos). Imagina que estás sujetando el eje para que la rueda quede delante de ti, tu mano derecha está a la derecha de la rueda y tu mano izquierda está a la izquierda de la rueda.

Figura\(\PageIndex{3}\): Una rueda que gira sobre un eje, con una velocidad angular horizontal (izquierda). Si intenta inclinar el eje como se muestra en el panel derecho, cambiando el momento angular de la rueda, también necesitará ejercer un par en la dirección vertical (que se muestra en la parte inferior derecha).

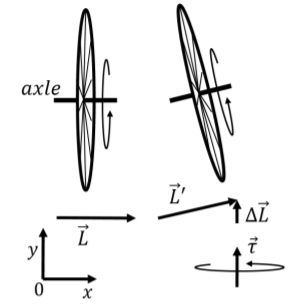
Definimos un sistema de coordenadas como se muestra para que la rueda esté girando como se muestra en el panel izquierdo, con la velocidad angular (y el momento angular) en la\(x\) dirección positiva (la parte superior de la rueda viene hacia ti).

Luego intenta levantar la mano derecha mientras baja la mano izquierda para inclinar el eje de rotación, como se muestra en el panel derecho. Al hacerlo, se cambia la dirección del momento angular (y la velocidad angular) de la rueda de tal manera que el momento angular,\(\vec L'\), ahora tiene una componente vertical,\(\Delta \vec L\), como se muestra. El par que se requiere para cambiar el momento angular viene dado por:\[\begin{aligned} \vec \tau = \frac{d\vec L}{dt} \sim \frac{\Delta \vec L}{\Delta t}\end{aligned}\] donde\(\Delta t\) está el tiempo que se tarda en cambiar el eje de rotación. El par requerido para cambiar el eje de rotación se dirige en la misma dirección que\(\Delta \vec L\) (la\(y\) dirección positiva). Es decir, no podrás simplemente inclinar el eje como se muestra; si quieres inclinar el eje, también necesitarás empujar hacia adelante con la mano derecha y tirar hacia atrás con la mano izquierda para ejercer el par requerido (¡mostrado en la parte inferior derecha de la figura)! Si simplemente intentas inclinar el eje de rotación, tu mano derecha será empujada hacia ti y tu mano izquierda lejos de ti, ¡como reacción al par que de otro modo se requeriría para inclinar el eje!

Conservación del momento angular

En la sección anterior, vimos que el par externo neto que se ejerce sobre un objeto (o sistema) es igual a la tasa de cambio de su momento angular:\[\begin{aligned} \frac{d\vec L}{dt} = \vec \tau^{ext}\end{aligned}\] donde el momento angular y el par se miden alrededor del mismo eje o punto de rotación, fijados en un marco inercial de referencia.

El momento angular total de un sistema alrededor de un punto de rotación se conserva (es decir, no cambia con el tiempo) si no se ejerce un par externo neto sobre el sistema alrededor de ese punto. Si uno hace que el sistema sea lo suficientemente grande, entonces todos los pares pueden tomarse para ser internos, y el momento angular del sistema se conserva. Así se conserva el momento angular del Universo alrededor de un punto fijo.

La conservación del momento angular es otra ley de conservación que derivamos de la Segunda Ley de Newton. En la formulación moderna de la física, entendemos que la conservación del momento angular se asocia con la simetría rotacional de la Segunda Ley de Newton; no importa desde qué “ángulo” modelaremos un sistema, siempre podemos usar la Segunda Ley de Newton. De igual manera, la conservación del impulso lineal se asocia con la simetría traslacional y la conservación de la energía se asocia con el hecho de que la Segunda Ley de Newton no cambia con el tiempo. El momento angular es fundamentalmente diferente al momento lineal y la energía, y se conserva bajo diferentes condiciones. El momento angular de un sistema alrededor de un eje/punto dado se conserva si no hay un par neto en el sistema alrededor de ese eje/punto.

Ejemplo\(\PageIndex{3}\)

Durante un giro, un patinador artístico acerca sus brazos a su cuerpo y aumenta su velocidad angular desde\(\omega_1\) to \(\omega_2\). By what fraction did his moment of inertia decrease in doing so?

Solución:

Podemos considerar que el eje de rotación es vertical a través del centro del patinador. Cuando el patinador artístico está girando, no hay un par externo neto sobre él. Así, su impulso angular se conserva a medida que trae sus brazos. A medida que introduce sus brazos, su momento de inercia disminuye, ya que está acercando la masa de sus brazos al eje de rotación. Si\(I_1\) y\(I_2\) son los momentos de inercia del patinador antes y después de brincar sus brazos, respectivamente, podemos escribir el momento angular alrededor de su eje de rotación como:\[\begin{aligned} L_1 &= I_1\omega_1\\ L_2 &= I_2\omega_2\end{aligned}\] Dado que no hay torque externo en el patinador, el momento angular es el mismo antes y después de que cambie su momento de inercia:\[\begin{aligned} L_1 &= L_2\\ I_1\omega_1 &= I_2\omega_2\\ \therefore \frac{I_1}{I_2} &= \frac{\omega_2}{\omega_1}\end{aligned}\]

Discusión:

Un patinador artístico giratorio es un buen ejemplo de la conservación del momento angular. Al cambiar su forma, pueden cambiar su momento de inercia y así su velocidad angular.

Ejemplo\(\PageIndex{4}\)

Demostrar que la Segunda Ley de Kepler es equivalente a una declaración sobre la conservación del momento angular de un planeta que orbita el Sol.

Solución:

La Segunda Ley de Kepler establece que en un periodo de tiempo\(\Delta t\), el área\(\Delta A\), que es barrida por un planeta es constante, independientemente de dónde se encuentre a lo largo de su órbita. En otras palabras:\[\begin{aligned} \frac{\Delta A}{\Delta t} = \text{constant}\end{aligned}\] La figura\(\PageIndex{4}\) muestra un planeta en órbita elíptica alrededor del sol.

Figura\(\PageIndex{4}\): El área barrida por un planeta en un periodo de tiempo\(dt\).

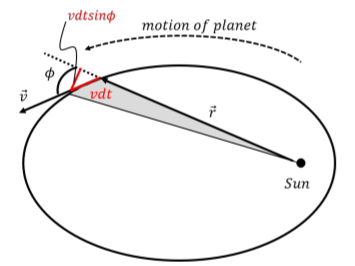
En algún momento, el planeta tiene un vector de velocidad\(\vec v\) y un vector de posición en\(\vec r\) relación con el Sol. En un pequeño periodo de tiempo\(dt\), el planeta se moverá a lo largo de una corta distancia\(vdt\), que podemos tomar como línea recta si\(dt\) es lo suficientemente pequeña. Dejar\(\phi\) ser el ángulo entre los vectores de velocidad y posición cuando estos son cola a cola, como se ilustra.

La pequeña cantidad de área,\(dA\), barrida por el planeta en un periodo de tiempo\(dt\), viene dada por el área del triángulo de ángulo recto con altura\(r\) y base\(vdt\sin\phi\)¹:\[\begin{aligned} dA = \frac{1}{2} r vdt\sin\phi\end{aligned}\] La velocidad a la que se barre el área es así:\[\begin{aligned} \frac{dA}{dt} = \frac{1}{2} r v\sin\phi\end{aligned}\] Consideremos ahora la magnitud del momento angular del planeta sobre el Sol:\[\begin{aligned} L = rp\sin\phi = rmv\sin\phi\end{aligned}\] donde está la masa del planeta\(m\). La velocidad a la que el planeta barre el área se puede escribir en términos del momento angular del planeta:\[\begin{aligned} \frac{dA}{dt} &= \frac{1}{2} r v\sin\phi = \frac{L}{2m}\end{aligned}\] La única fuerza que se ejerce sobre el planeta es la fuerza gravitacional del Sol. Esa fuerza siempre es antiparalela al vector\(\vec r\) del Sol al planeta, y no puede resultar en un par en el planeta alrededor del Sol. Así, el momento angular del planeta alrededor del Sol debe conservarse, y\(L\) es constante. A su vez, esto significa que la velocidad a la que el área es barrida por el planeta, que es proporcional a\(L\), también es constante. Así, la Segunda Ley de Kepler equivale a decir que el momento angular de un planeta relativo al Sol es constante.

Notas al pie

1. Esto sólo es exacto en el límite de\(dt\to 0\), cuando el área pequeña de la pieza extra fuera de la elipse se desvanece.