13.4: El movimiento de un péndulo

En esta sección, mostramos cómo y cuándo el movimiento de un péndulo puede describirse como simple movimiento armónico. Considera el simple péndulo que se construye a partir de una cuerda de longitud sin masa,\(L\), unida a un punto fijo en un extremo y a una masa puntual\(m\) en el otro, como se ilustra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un péndulo simple que oscila en un plano vertical.

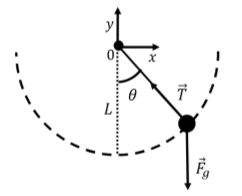
El péndulo puede oscilar en el plano vertical, y hemos mostrado nuestra elección de sistema de coordenadas (el\(z\) eje, no mostrado, está fuera de página). Las únicas dos fuerzas sobre la masa son la tensión de la cuerda y su peso. Podemos describir la posición de la masa por el ángulo,\(\theta(t)\), que la cuerda hace con la vertical. Podemos modelar la dinámica del péndulo simple considerando el par neto y la aceleración angular alrededor del eje de rotación que es perpendicular al plano de la página y que pasa por el punto de la cuerda que se fija.

La fuerza de tensión no puede crear un par en la masa alrededor del eje de rotación, ya que es antiparalela al vector desde el punto de rotación a la masa. El par neto es así el par de torsión de la fuerza de gravedad:\[\begin{aligned} \vec\tau^{net} &=\vec \tau_g \\ &=\vec r \times \vec F_g = (L\sin\theta \hat x - L\cos\theta \hat y) \times (-mg\hat y)\\ &=-mgL\sin\theta \hat z\end{aligned}\] donde\(L\) está la magnitud del vector,\(\vec r\), desde el eje de rotación hasta donde se ejerce la fuerza de gravedad. El par neto es igual a la aceleración angular\(\alpha\), multiplicada por el momento de inercia,\(I\), de la masa:\[\begin{aligned} \vec\tau^{net} &= I\vec\alpha\\ -mgL\sin\theta \hat z&= mL^2 \vec\alpha\\ -g\sin\theta \hat z&= L \vec\alpha\end{aligned}\] donde\(I=ML^2\) está el momento de inercia para una masa puntual a una\(L\) distancia del eje de rotación. Para la posición ilustrada en la Figura\(\PageIndex{1}\), la aceleración angular del péndulo está en la\(z\) dirección negativa (hacia la página) y corresponde a un movimiento en sentido horario para el péndulo, como cabría esperar. La aceleración angular es la derivada por segunda vez del ángulo,\(\theta\): Así\[\begin{aligned} \alpha = \frac{d^2\theta}{dt^2}\end{aligned}\] podemos reescribir la ecuación que obtuvimos de la versión de dinámica rotacional de la Segunda Ley de Newton como:\[\begin{aligned} -g\sin\theta \hat z&= L \vec\alpha\\ \frac{d^2\theta}{dt^2} &= -\frac{g}{L}\sin\theta\end{aligned}\] donde solo usamos las magnitudes en la segunda ecuación, ya que todas las las cantidades angulares están en la\(z\) dirección. Esta ecuación de movimiento para\(\theta(t)\) casi se parece a la ecuación para simple oscilación armónica para el ángulo\(\theta\) (excepto que tenemos\(\sin\theta\) en lugar de\(\theta\)). Sin embargo, considere la “aproximación de ángulo pequeño” ¹ para la función seno:\[\begin{aligned} \sin\theta \approx \theta \end{aligned}\] Si las oscilaciones del péndulo son “pequeñas”, de tal manera que la aproximación de ángulo pequeño es válida, entonces la ecuación de movimiento para el péndulo es:\[\begin{aligned} \frac{d^2\theta}{dt^2} &= -\frac{g}{L}\sin\theta \approx -\frac{g}{L}\theta \\ \therefore \frac{d^2\theta}{dt^2} &=-\frac{g}{L}\theta \quad (\text{for small }\theta)\end{aligned}\] y el ángulo que el péndulo hace con la vertical se describe por la ecuación para oscilación armónica simple con frecuencia angular:\[\begin{aligned} \omega = \sqrt{\frac{g}{L}}\end{aligned}\] El ángulo\(\theta\),, en función del tiempo es así descrito por la función:\[\begin{aligned} \theta(t) = \theta_{max}\cos(\omega t +\phi)\end{aligned}\] donde\(\theta_{max}\) está la amplitud máxima de las oscilaciones y \(\phi\)es una fase que depende de cuándo elegimos definir\(t=0\).

Ejercicio\(\PageIndex{1}\)

Kaiden construyó un reloj de abuelo usando un simple péndulo, pero encontró que el período era el doble de lo que quería que fuera. Para reducir a la mitad el periodo del péndulo, puede

1. cambiar la masa.
2. reducir a la mitad la longitud de la cuerda.
3. cuarto de la longitud de la cuerda.
4. el doble de la longitud de la cuerda.
5. cuadruplicar la longitud de la cuerda.

Responder

El péndulo físico

Un péndulo físico se define como cualquier objeto al que se le permite rotar en el plano vertical alrededor de algún eje que atraviesa el objeto, como se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Péndulo físico que oscila en un plano vertical alrededor de un eje a través del objeto.

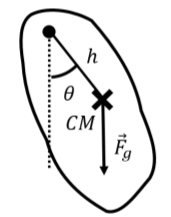
Las únicas fuerzas ejercidas sobre el péndulo son su peso (ejercido en su centro de masa) y una fuerza de contacto ejercida en el eje de rotación. El péndulo físico puede modelarse exactamente de la misma manera que el péndulo simple, excepto que utilizamos el momento de inercia del objeto alrededor del eje de rotación. Solo el peso resulta en un par alrededor del eje de rotación, ya que la fuerza de contacto se ejerce en el eje de rotación:\[\begin{aligned} \tau^{net} = \tau_g &= I\alpha\\ -mgh\sin\theta &= I\alpha = I \frac{d^2\theta}{dt^2}\end{aligned}\] donde\(h\) está la distancia desde el eje de rotación hasta el centro de masa. En la aproximación de ángulo pequeño, esto se convierte en:\[\begin{aligned} \frac{d^2\theta}{dt^2} &=-\frac{mgh}{I}\theta \quad (\text{for small }\theta)\end{aligned}\] y encontramos que el péndulo físico oscila con una frecuencia angular:\[\begin{aligned} \omega = \sqrt{\frac{mgh}{I}}\end{aligned}\]

Notas al pie

1. ¡Busca la función sinusoidal en la serie Maclaurin/Taylor!