14.2: Descripción matemática de una ola

Para describir el movimiento de una onda a través de un medio, podemos describir el movimiento de las partículas individuales del medio a medida que pasa la onda. Específicamente, describimos la posición de cada partícula utilizando su desplazamiento,\(D\), desde su posición de equilibrio. Considere nuestro ejemplo de cuerda en el que una onda sinusoidal se propaga a través de un medio (la cuerda) en la\(x\) dirección positiva, como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): El desplazamiento (\(D\)) de puntos en diferentes posiciones (\(x\)) en una cuerda a medida que pasa una onda sinusoidal.

El desplazamiento,\(D\), de cada punto en posición,\(x\), en el medio se muestra en el eje vertical de la Figura\(\PageIndex{2}\). La línea negra continua corresponde a una instantánea de la onda en el momento\(t=0\). La onda tiene una amplitud,\(A=5\text{m}\), una velocidad\(v=1\text{m/s}\), y una longitud de onda,\(\lambda=4\text{m}\). La línea punteada corresponde a una instantánea de la ola un segundo después, a\(t=1\text{s}\), cuando la ola se ha movido a la derecha por una distancia\(vt=1\text{m}\).

Figura\(\PageIndex{2}\): Desplazamiento en función de la posición de las partículas en un medio a medida que pasa una onda. La línea punteada muestra el desplazamiento en función del tiempo\(1\text{ s}\) después de la línea continua, y corresponde a una ola que viaja hacia la derecha.

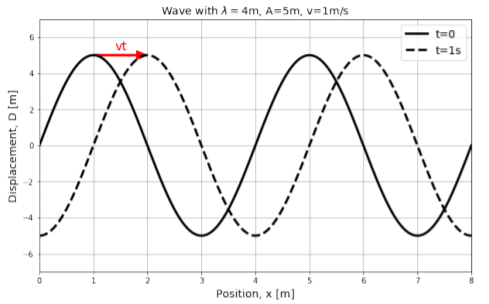
Es importante señalar que la Figura no\(\PageIndex{2}\) se limita a describir ondas transversales, aunque la ilustración sugiere que los desplazamientos de las partículas (eje vertical) son perpendiculares a la dirección de propagación de la onda (horizontal). La cantidad,\(D\), que se traza en el eje vertical corresponde al desplazamiento de una partícula desde su posición de equilibrio. Ese desplazamiento podría corresponder al desplazamiento longitudinal de una partícula en una onda longitudinal.

En el tiempo\(t=0\) (línea continua), el desplazamiento de cada punto en el medio\(D(x, t=0)\), en función de su distancia desde el origen\(x\), puede describirse mediante una función sinusoidal:

\[D(x,t=0)=A\sin\left(\frac{2\pi}{\lambda}x \right) \]

Esto corresponde a que el desplazamiento sea 0 en el origen y en cualquier posición,, es decir\(x\), un múltiplo de la longitud de onda,\(\lambda\).

Si la onda se mueve con velocidad\(v\) en la\(x\) dirección positiva, entonces en el momento\(t\), la función sinusoidal en la Figura\(\PageIndex{2}\) se habrá desplazado hacia la derecha en una cantidad\(vt\) (línea punteada). El desplazamiento de un punto ubicado en la posición\(x\) en el momento\(t\) será el mismo que el desplazamiento del punto en posición\(x-vt\) en el momento\(t=0\). Por ejemplo, en\(\PageIndex{2}\) la Figura el desplazamiento del punto\(x=2\text{m}\) en el tiempo\(t=1\text{s}\) es el mismo que el desplazamiento del punto en posición\(x-vt=1\text{m}\) en\(t=0\).

Podemos afirmar esta condición como: Es\[\begin{aligned} D(x,t) = D(x-vt, t=0)\end{aligned}\] decir, en algún momento\(t\), el desplazamiento de un punto en posición\(x\) se encuentra encontrando la posición del punto en\(x-vt\) at\(t=0\). Ya tenemos una ecuación para encontrar el desplazamiento de un punto en\(t=0\). Usando la condición anterior, podemos modificar la Ecuación 14.2.1 para escribir una función para el desplazamiento de un punto en la posición\(x\) en el momento\(t\):\[\begin{aligned} D(x,t) = A\sin\left( \frac{2\pi}{\lambda}(x-vt) \right)\end{aligned}\] Observando que\(v/\lambda= 1/T\), podemos escribir esto como:\[\begin{aligned} D(x,t) = A\sin\left( \frac{2\pi x}{\lambda}- \frac{2\pi t}{T} \right)\end{aligned}\] En la derivación anterior, nosotros asumió que en su momento\(t=0\), el desplazamiento en\(x=0\) era\(D(x=0, t=0)=0\). En general, el desplazamiento podría tener cualquier valor en\(x=0\) y\(t=0\), así podemos permitir que la onda se desplace hacia la izquierda o hacia la derecha incluyendo una fase,\(\phi\), que se puede determinar a partir del desplazamiento en\(x=0\) y\(t=0\):

\[ D(x,t) = A\sin\left(\frac{2\pi x}{\lambda}-\frac{2\pi t}{T}+\phi \right)\]

donde\(\phi=0\) corresponde que el desplazamiento sea cero en\(x=0\) y\(t=0\).

Ejercicio\(\PageIndex{1}\)

Cuál es el valor de la fase\(\phi\) if the displacement of the point at \(x=0\) is \(D=A/2\) at time \(t=0\)?

1. \(\pi/6\).
2. \(\pi/4\).
3. \(\pi/3\).
4. \(\pi/2\).

Contestar

La ecuación anterior está escrita en términos de la longitud de onda\(\lambda\), y el período,\(T\), de la onda. A menudo, se utiliza el “número de onda”\(k\), y la “frecuencia angular”\(\omega\), para describir la onda. Estos se definen como:

\[k=\frac{2\pi}{\lambda}\]

\[\omega = \frac{2\pi}{T}\]

Usando el número de onda y la frecuencia angular elimina los factores de\(2\pi\) en la expresión for\(D(x,t)\), que ahora se puede escribir como:

\[D(x,t)=A\sin (kx-\omega t+\phi )\]

Es importante señalar que el número de onda,\(k\), no tiene relación con la constante de resorte que utilizamos para los resortes.

Usando la Ecuación 14.1.1, también podemos relacionar el número de onda y la frecuencia angular con la velocidad de la onda:

\[\begin{aligned} v = \frac{\lambda}{T}=\frac{\frac{2\pi}{k}}{\frac{2\pi}{\omega}}=\frac{\omega}{k}\end{aligned}\]

La Ecuación de Onda

En el Capítulo 13, vimos que cualquier sistema físico cuya posición,\(x\), satisfaga la siguiente ecuación:\[\begin{aligned} \frac{d^2x}{dt^2}=-\omega^2 x\end{aligned}\] sufrirá un simple movimiento armónico con frecuencia angular\(\omega\), y que\(x(t)\) puede modelarse como:\[\begin{aligned} x(t) = A\cos(\omega t + \phi)\end{aligned}\]

De igual manera, cualquier sistema, donde el desplazamiento de una partícula en función de la posición y el tiempo\(D(x,t)\),, satisface la siguiente ecuación:

\[\frac{\partial ^{2}D}{\partial x^{2}}=\frac{1}{v^{2}}\frac{\partial ^{2}D}{\partial t^{2}}\]

se describe por una onda que se propaga con una velocidad\(v\). La ecuación anterior se llama la “ecuación de onda unidimensional” y se obtendría a partir del modelado de la dinámica del sistema, así como la ecuación de movimiento para un oscilador armónico simple se puede obtener a partir de la Segunda Ley de Newton. Para el oscilador armónico, las propiedades del sistema (por ejemplo, masa y constante de resorte) determinan la frecuencia angular,\(\omega\). Para una ola, las propiedades del medio determinan la velocidad de la ola,\(v\).

Utilizamos derivadas parciales en la ecuación de onda en lugar de derivadas totales porque\(D(x,t)\) es multivariante. Una posible solución a la ecuación de onda unidimensional es:\[\begin{aligned} D(x,t) = A\sin\left( kx -\omega t + \phi \right)\end{aligned}\] que es la función que usamos en la sección anterior para describir una onda sinusoidal.

Además, si existen múltiples soluciones a la ecuación de onda\(D_1(x,t)\)\(D_2(x,t)\),,, etc, entonces cualquier combinación lineal,\(D(x,t)\), de las soluciones también será una solución a la ecuación de onda:\[\begin{aligned} D(x,t) = a_1D_1(x,t)+a_2D_2(x,t)+a_3D_3(x,t)+\dots\end{aligned}\] Esta última propiedad se llama “el principio de superposición”, y es siendo el resultado de la ecuación de onda lineal en\(D\) (no depende\(D^2\), por ejemplo). Es fácil comprobar, por ejemplo, que si\(D_1(x,t)\) y\(D_2(x,t)\) satisfacer la ecuación de onda, también lo hace su suma.

En tres dimensiones, el desplazamiento de una partícula en el medio depende de sus tres coordenadas espaciales\(D(x,y,z,t)\), y la ecuación de onda en coordenadas cartesianas viene dada por:

\[\begin{aligned} \frac{\partial ^{2}D}{\partial x^{2}}+\frac{\partial ^{2}D}{\partial y^{2}}+\frac{\partial ^{2}D}{\partial z^{2}}&=\frac{1}{v^2}\frac{\partial ^{2}D}{\partial t^{2}}\\\end{aligned}\]

Existen muchas funciones que pueden satisfacer esta ecuación, y la mejor elección dependerá del sistema físico que se modele y de las propiedades de la onda que se desee describir.