15.1: Presión

La presión ejercida por una fuerza\(\vec F\), sobre una superficie con área\(A\), es una cantidad escalar\(P\), definida como:

\[\begin{aligned} P=\frac{F_{\perp}}{A}\end{aligned}\]

donde\(F_{⊥}\) es el componente de la fuerza perpendicular a la superficie. La unidad SI para presión es el Pascal (Pa). La presión está relacionada con el área\(A\),, sobre la cual se ejerce una fuerza, y puede pensarse como una medida de cuán concentrada está esa fuerza. Por ejemplo, una fuerza\(10\text{ N}\) ejercida a través de una aguja (un área pequeña) resultará en una presión mucho mayor que si esa fuerza fuera ejercida por una mano plana (un área más grande).

Cuando se ejerce una fuerza sobre un fluido, crea una presión que modelizamos como estar en todas partes en el fluido. Para cada elemento en el fluido, la presión del fluido circundante ejerce una fuerza hacia dentro sobre el elemento desde todas las direcciones (ver Figura\(\PageIndex{1}\)). En reacción, el elemento ejerce una fuerza hacia afuera en todas las direcciones, y estas fuerzas actúan sobre los elementos vecinos.

Esto es algo análogo a la tensión que existe en todas partes en una cuerda, donde cada elemento de la cuerda experimenta fuerzas de los elementos vecinos en la cuerda que intentan “separarla”. La presión puede pensarse como una tensión “negativa”, en el sentido de que el material bajo presión está experimentando fuerzas que intentan colapsar el elemento sobre sí mismo, en lugar de intentar separarlo. Para crear una tensión en una cuerda, se ejercería una fuerza hacia afuera sobre la cuerda (con el fin de estirarla), de manera que la cuerda ejerza una fuerza hacia adentro en reacción. Para crear presión en un fluido, se debe ejercer una fuerza hacia adentro sobre el fluido, que luego ejerce una fuerza hacia afuera en reacción.

Si consideramos un pequeño volumen cúbico de fluido, como se representa en el centro de la Figura\(\PageIndex{1}\), ese elemento de fluido experimentará fuerzas hacia adentro en todas las direcciones a partir de la presión en el fluido circundante, como lo ilustran las flechas. Si las fuerzas de la presión resultan en ninguna fuerza neta sobre el elemento fluido, entonces decimos que el fluido está en equilibrio hidrostático, y el elemento de fluido estará en reposo en un marco inercial de referencia.

Figura\(\PageIndex{1}\): Un pequeño elemento dentro de un fluido con presión no experimentará fuerza neta por la presión en el fluido, ya que la fuerza asociada a la presión en el fluido se ejerce en todas las direcciones.

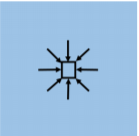
Considere, en cambio, un elemento de fluido que en el borde de un recipiente para el fluido (por ejemplo, una taza de agua), como se representa en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): En el borde de un contenedor, un pequeño elemento de fluido ejercerá una fuerza hacia afuera sobre el contenedor, y el contenedor ejercerá una fuerza hacia adentro sobre el elemento de fluido.

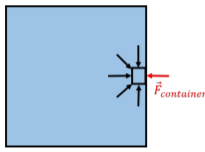
En este caso, no hay fluido en el lado derecho del elemento fluido para ejercer una fuerza hacia la izquierda. Si el elemento fluido está en equilibrio, entonces debe ser el contenedor el que ejerza esa fuerza,\(\vec F\) contenedor, sobre el fluido. Por la Tercera Ley de Newton, el elemento de fluido ejerce una fuerza hacia afuera sobre el contenedor. Esto es cierto en todos los puntos de la superficie del contenedor, que todos experimentarán una fuerza hacia afuera por la presión del fluido. Si la presión es constante sobre una superficie, la magnitud de la fuerza hacia afuera sobre la superficie será igual a la presión del fluido multiplicada por el área de esa superficie.

Si coloca una lata sellada vacía bajo el agua, el agua ejercerá una presión sobre todas las superficies de la lata que conducirá a una fuerza neta hacia adentro en todas las superficies de la lata. Si la presión del agua es lo suficientemente alta, la lata se aplastará. Si, por otro lado, se permite que la lata se llene de agua, no se aplastará, ya que el agua dentro de la lata tendrá la misma presión que el agua fuera de la lata y ejercerá una fuerza neta igual hacia afuera en todas las superficies de la lata. La fuerza neta en cada superficie de la lata será cero, y la lata no se aplastará, por muy alta que sea la presión del agua.

En general, si hay una interfaz con el fluido a cada lado de la misma una presión diferente, es la diferencia de presión a cada lado de la interfaz la que determina la fuerza neta ejercida sobre la interfaz, en lugar de la presión absoluta.

Ejercicio\(\PageIndex{1}\)

Coloca una lata sobre una mesa y usas una bomba para crear un vacío dentro de la lata. Observa que la lata se aplasta. ¿Qué explicación es correcta?

1. Al succionar el aire de la lata, también succiona las paredes de la lata.
2. Se baja la presión dentro de la lata para que el aire fuera de la lata ejerza una fuerza mayor hacia adentro sobre la lata que la fuerza hacia afuera del aire dentro de la lata.
3. Se baja la presión dentro de la lata para que el aire dentro de la lata ejerza una fuerza de tracción sobre las paredes de la lata.
4. Todo lo anterior son todas formas válidas de modelar esto.

Contestar

El efecto de la gravedad

Al discutir la Figura\(\PageIndex{1}\), argumentamos que el fluido ejerce una fuerza igual, desde todas las direcciones, sobre el elemento fluido, de manera que la fuerza neta sobre el elemento fluido es cero. Esto no es del todo correcto ante la presencia de la gravedad, donde el elemento fluido tendrá un peso. Por lo tanto, si el elemento fluido va a estar en equilibrio, la fuerza ascendente (y presión) del fluido de abajo debe ser mayor que la del fluido por encima del elemento fluido.

La figura\(\PageIndex{3}\) muestra un elemento de fluido que tiene una altura\(h\) y una superficie\(A\) en el plano horizontal. La presión,\(P_{2}\), en el fluido por debajo del elemento fluido debe ser mayor que la presión,\(P_{1}\), por encima del elemento fluido, si el elemento fluido está en equilibrio.

Figura\(\PageIndex{3}\): En presencia de gravedad, la presión por debajo de un elemento de fluido debe ser mayor para que el elemento fluido se mantenga en equilibrio.

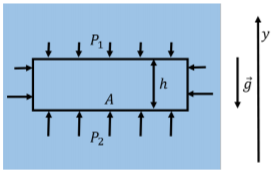
El elemento de fluido tiene una masa total,\(m\), dada por:

\[\begin{aligned} m = \rho V = \rho Ah \end{aligned}\]

donde,\(V = Ah\), es el volumen del fluido, y,\(ρ\), su densidad.

La fuerza neta (horizontal) ejercida por el fluido externo sobre el elemento fluido es cero a lo largo de las superficies verticales. Dejar\(P_{1}\) ser la presión en el fluido por encima del elemento fluido, y\(P_{2}\) ser la presión por debajo del elemento fluido. Si elegimos un eje y que sea positivo hacia arriba y el elemento fluido no acelera en la dirección vertical, entonces el componente y de la Segunda Ley de Newton, escrito para el elemento fluido, es:

\[\begin{aligned} &\sum F_{y} =F_{2}-F_{1}-mg=0 \\ &P_{2}A-P_{1}A-mg=0 \\ &P_{2}A-P_{1}A-\rho Ahg=0 \\ &\therefore P_{2}-P_{1}=\rho gh \end{aligned}\]

donde se utilizó el hecho de que la fuerza resultante de una presión viene dada por la presión multiplicada por el área sobre la que se ejerce. Así encontramos que la diferencia de presión debida a la gravedad en un fluido entre dos posiciones,\(y_{2}\) y\(y_{1}\), viene dada por:

\[P(y_{2})-P(y_{1})=-\rho g(y_{2}-y_{1})\]

donde el\(y\) eje se define para aumentar en la dirección hacia arriba. Dado que la presión en el fluido depende de la ubicación en el fluido, decimos que hay un “gradiente de presión” en el fluido.

Ejercicio\(\PageIndex{2}\)

Figura\(\PageIndex{4}\): Retención de agua en una pajita vertical.

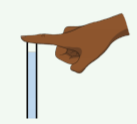
Usas tu dedo para bloquear el extremo superior de una pajita y luego retirar la pajita de un vaso de agua. ¿Cuál es la descripción más correcta de por qué el agua permanece en la pajita (Figura\(\PageIndex{4}\)) antes de soltar el dedo?

1. La pajita no puede tener vacío dentro de ella; a menos que se retire el dedo para dejar entrar aire para reemplazar el agua, el agua permanecerá en la paja.
2. Hay una pequeña cantidad de vacío por encima del agua que succiona el agua hacia arriba y evita que se salga.
3. La presión del aire en la paja debajo del agua es mayor que la presión del aire en la paja por encima del agua.
4. La presión del aire en la paja debajo del agua es menor que la presión del aire en la paja por encima del agua.

Contestar

Hemos asumido que la densidad del fluido,, es constante\(ρ\), y que el fluido no puede comprimirse. Esta es una muy buena aproximación para un líquido como el agua, pero no para un gas, cuya densidad dependerá de su presión. Si el fluido fuera un gas (por ejemplo, una columna de aire en nuestra atmósfera), tanto la densidad como la presión cambiarán en función de la altura. Podemos tomar esto en cuenta fácilmente en nuestro modelo, si consideramos que el elemento fluido tiene una altura muy pequeña,\(dy\), en lugar de la altura finita\(h\),, como en la derivación anterior. Un elemento fluido con una altura infinitesimal,\(dy\), se ilustra en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Gradiente de presión de la gravedad sobre un elemento fluido infinitesimal.

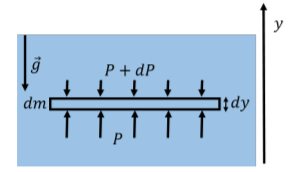
En la altura muy pequeña\(dy\),, la densidad del fluido,\(ρ\), se puede tomar como constante, y el elemento infinitesimal del fluido tendrá una masa\(dm\):

\[\begin{aligned} dm=\rho Ady \end{aligned}\]

Podemos modelar la presión ejercida por el fluido por encima del elemento fluido como\(P + dP\), y la presión ejercida por el fluido de abajo como\(P\), donde\(dP\) hay un pequeño cambio (negativo) en la presión ¹. El\(y\) componente de la Segunda Ley de Newton escrita para el elemento fluido infinitesimal es así:

\[\begin{aligned} \sum F_{y} = PA-(P+dP)A-dmg &=0 \\ PA-PA-dPA-\rho Adyg&=0 \\ \therefore - dP - \rho gdy &=0 \end{aligned}\]

Así podemos determinar cómo cambia la presión con la altura,\(y\):

\[\frac{dP}{dy}=-\rho g\]

Esto nos dice que la tasa de cambio de presión con el aumento\(y\) es negativa; es decir, la presión disminuye a medida que aumenta la elevación, como ya habíamos concluido. Podemos integrar la ecuación para obtener el cambio de presión al pasar de\(y_{1}\) a\(y_{2}\):

\[\begin{aligned} dP&=-\rho gdy \\ \int_{P_{1}}^{P_{2}}dp&=-\int_{y_{1}}^{y_{2}}\rho gdy \\ \therefore P_{2}-P_{1}&= - \int_{y_{1}}^{y_{2}}\rho gdy \end{aligned}\]

Si la densidad,\(ρ\), es constante, entonces esto lleva a la Ecuación 15.1.1. Tenga en cuenta que, hasta el momento, solo hemos modelado cómo la presión en un fluido cambia con la altura, pero no hemos determinado la presión absoluta en un fluido.

Ejemplo\(\PageIndex{1}\)

Si asumimos que la densidad del aire es proporcional a su presión, ¿cómo cambia la densidad del aire con la altitud?

Solución:

Sabemos que la tasa de cambio de presión con altitud (posición\(y\), donde positivo\(y\) se define como ascendente) viene dada por:

\[\begin{aligned}\frac{dP}{dy}=-\rho g \end{aligned}\]

Como podemos suponer que la densidad es proporcional a la presión, podemos introducir una constante arbitraria\(a\), y afirmar que:

\[\begin{aligned} \rho &=aP \\ \therefore \frac{dP}{dy}&=\frac{d}{dy}\frac{1}{a}\rho = \frac{1}{a}\frac{d\rho}{dy} \end{aligned}\]

donde la constante\(a\) puede ser evaluada si conocemos la presión y densidad en algún momento. Podemos escribir así que la tasa de cambio de la densidad con posición\(y\) viene dada por:

\[\begin{aligned} \frac{1}{a}\frac{d\rho}{dy}&=-\rho g \\ \therefore \frac{d\rho}{dy}&=-ag\rho \end{aligned}\]

Esta es una ecuación diferencial separable para\(ρ\), que nos permite separar las variables e integrarnos de, digamos, una altitud de\(y = 0\), donde está la densidad\(ρ_{0}\), a una altitud\(y\), donde la densidad es\(ρ\):

\[\begin{aligned} \frac{d\rho}{\rho}&=-agdy \\ \int_{\rho_{0}}^{\rho}\frac{d\rho}{\rho}&=-\int_{0}^{y}agdy \\ \ln (\rho)-\ln (\rho _{0})&=-agy \\ \ln\left(\frac{\rho}{\rho _{0}} \right)&=-agy \end{aligned}\]

Podemos tomar el exponencial en cada lado de la ecuación para deshacernos del logaritmo:

\[\begin{aligned} \frac{\rho}{\rho_{0}}&=e^{-agy} \\ \therefore \rho (y)&=\rho _{0}e^{-agy} \end{aligned}\]

Encontramos así que la densidad del aire disminuye exponencialmente con la altitud. Por ello es más difícil respirar a gran altura. Dado que asumimos que la densidad del aire es proporcional a su presión, la presión del aire también disminuirá exponencialmente con el aumento de la altitud:

\[\begin{aligned} P(y)=P_{0}e^{-agy} \end{aligned}\]

donde\(P_{0}\) esta la presión a una altitud de\(y = 0\). Si sabemos\(P_{0}\) y\(ρ_{0}\), entonces la constante\(a\) viene dada por:

\[\begin{aligned} a=\frac{\rho _{0}}{P_{0}} \end{aligned}\]

Discusión:

Si aplicáramos este modelo a la atmósfera terrestre, nuestro modelo sólo proporcionaría un acuerdo cualitativo, ya que la densidad del aire también depende de su temperatura y otros factores. Sin embargo, es interesante que, a partir del simple requisito de que un elemento del aire esté en equilibrio hidrostático, podamos obtener una descripción razonable de cómo la presión y la densidad cambian con la altitud en la atmósfera terrestre.

Principio de Pascal

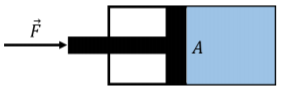
El Principio de Pascal establece que si se ejerce una presión externa sobre un fluido, la presión en todas partes del fluido aumenta en esa cantidad. Por ejemplo, si un fluido está contenido en un pistón con un área de sección transversal,\(A\), y una fuerza,\(F\), se ejerce sobre el pistón (Figura\(\PageIndex{6}\)), entonces la presión en todas partes en el fluido aumenta en\(F/A\).

Figura\(\PageIndex{6}\): Una fuerza ejercida sobre el pistón aumentará la presión en todas partes del fluido.

Si queremos determinar la presión absoluta en el agua a cierta profundidad,\(h\), en el océano, necesitamos incluir el hecho de que la atmósfera terrestre ejerce una fuerza neta descendente sobre la superficie del océano además de que la presión cambia con la profundidad debido a la gravedad. La presión del aire en la atmósfera terrestre se llama “presión atmosférica”, y depende de una variedad de condiciones, como el clima. La presión promedio de la atmósfera es\(P_{0} = 1.013 × 10^{5}\text{ Pa}\). Si la presión atmosférica está\(P_{0}\) en la superficie del océano, entonces la presión a cierta profundidad,\(h\), viene dada por:

\[\begin{aligned} P(h)=P_{0}+\rho gh \end{aligned}\]

donde\(ρ\) está la densidad del agua. Como consecuencia, la presión a cualquier profundidad,\(h\), en un fluido es la misma en todas partes a esa profundidad en el fluido.

Ejercicio\(\PageIndex{3}\)

Figura\(\PageIndex{7}\): Tres vasos con diferentes formas.

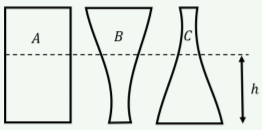
Llenas los tres vasos de la Figura de\(\PageIndex{7}\) tal manera que el líquido alcance una altura h por encima del fondo del vaso. ¿Qué se puede decir de la presión del líquido en el fondo de cada vaso?

1. Es más alto para el vidrio\(A\).
2. Es más alto para el vidrio\(B\).
3. Es más alto para el vidrio\(C\).
4. Es lo mismo para todas las gafas.
5. Sólo es lo mismo para todas las gafas si podemos descuidar la presión atmosférica.

Contestar

Ejemplo\(\PageIndex{2}\)

Figura\(\PageIndex{8}\): Fuerza ejercida sobre el pistón de un elevador hidráulico para dar vida a una masa\(M\).

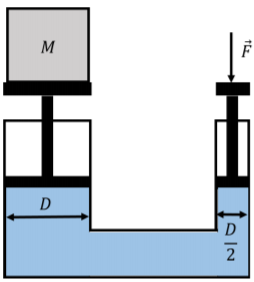
Un elevador hidráulico explota el principio de Pascal para usar una fuerza pequeña para ejercer una fuerza grande. El elevador hidráulico de la Figura\(\PageIndex{8}\) muestra un elevador que se construye al tener un fluido entre dos pistones móviles verticales. Los pistones son cilíndricos y el diámetro de sus secciones transversales son\(D\) y\(D/2\). Una masa,\(M\), se coloca sobre el pistón con el diámetro mayor. ¿Cuál es la magnitud de la fuerza,\(\vec F\), que se debe aplicar sobre el pistón más pequeño con el fin de levantar la masa,\(M\)?

Solución:

Si\(\vec F\) se aplica una fuerza al pistón pequeño, entonces la presión en el fluido aumentará en:

\[\begin{aligned} \Delta P = \frac{F}{A}=\frac{F}{\pi \frac{D^{2}}{4}}=\frac{4F}{\pi D^{2}}\end{aligned}\]

Esto dará como resultado una fuerza neta hacia arriba,\(\vec F'\), en el pistón grande, con una magnitud:

\[\begin{aligned} F' = \Delta P A' = \Delta \pi D^{2} = \frac{4F}{\pi D^{2}}\pi D^{2}=4F\end{aligned}\]

Así, la fuerza sobre el pistón grande será cuatro veces la que se ejerce sobre el pistón pequeño. Uno sólo necesita ejercer una fuerza con una magnitud\(Mg/4\) de para levantar la masa,\(M\).

Medición de la presión

En esta sección, describimos cómo se pueden diseñar instrumentos para medir la presión. El dispositivo más directo es un manómetro, el cual se construye utilizando un tubo en forma de U lleno de un fluido de densidad conocida\(ρ\), como se muestra en la Figura\(\PageIndex{9}\).

Figura\(\PageIndex{9}\): Un manómetro puede medir la diferencia entre una presión\(P\) y una presión atmosférica,\(P_{0}\). Esa diferencia se llama “presión manométrica”.

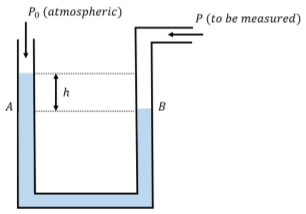
Un manómetro se puede utilizar para medir una presión\(P\) relativa a la presión atmosférica,\(P_{0}\). Un extremo del tubo está abierto a la presión atmosférica, y el otro está conectado al fluido (por ejemplo, un gas) para el cual queremos medir la presión. Si la presión que se mide es mayor que la presión atmosférica, el fluido en el manómetro experimentará una mayor fuerza descendente en el lado de la presión a medir que en el lado abierto a la presión atmosférica, como se muestra en la Figura\(\PageIndex{9}\). Habrá una diferencia,\(h\), en el nivel del fluido a cada lado del tubo, que es directamente proporcional a la diferencia de presión entre los dos lados del tubo.

Considere el punto en el fluido en la ubicación\(B\) de la Figura\(\PageIndex{9}\), donde está la presión\(P_{B} = P\), la presión a medir. El punto en el fluido en la ubicación\(A\), que está a la misma altura en el fluido, debe tener la misma presión que el punto\(B\). Podemos escribir la presión en el punto\(A, P_{A}\), como la suma de la presión atmosférica y la presión de la columna de agua de altura,\(h\):

\[\begin{aligned} P_{A}=P_{0}+\rho gh \end{aligned}\]

Dado que esto también debe ser igual a la presión en el punto\(B\), podemos encontrar la diferencia entre la presión que queremos medir y la presión atmosférica:

\[\begin{aligned} P_{A}&=P_{B} \\ P_{0}+\rho gh &=P \\ \therefore P-P_{0}&=\rho gh \end{aligned}\]

La diferencia entre una presión y la presión atmosférica se llama “presión manométrica”, y es todo lo que podemos medir si no conocemos el valor absoluto de la presión atmosférica. Usando un manómetro, la presión manométrica viene dada por\(ρgh\), mientras que la “presión absoluta”,\(P\), viene dada por la adición de la presión atmosférica a la presión manométrica,\(P = P_{0} + ρgh\). La mayoría de los dispositivos de medición de presión (“manómetros”), miden la presión relativa a la presión atmosférica, utilizando un mecanismo similar.

La presión atmosférica en un lugar de la Tierra varía según el clima. Un barómetro es un instrumento diseñado para medir la presión atmosférica. Se puede construir un barómetro simple a partir de un manómetro, con un extremo cerrado, como se ilustra en la Figura\(\PageIndex{10}\).

Figura\(\PageIndex{10}\): Barómetro construido a partir de un mamómetro para medir los cambios relativos en la presión atmosférica.

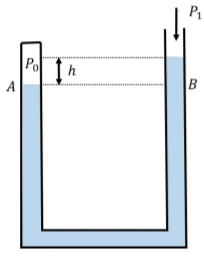
Un extremo del manómetro se sella en un día donde la presión atmosférica es, digamos,\(P_{0}\), mientras que el otro extremo del tubo se deja abierto. La diferencia de altura\(h\),, entre el fluido en cada lado del tubo es una medida de cuán diferente es la presión atmosférica actual,\(P_{1}\), relativa a la presión,\(P_{0}\), cuando se selló el manómetro. En la Figura\(\PageIndex{10}\), el barómetro se muestra en un día donde la presión atmosférica es menor que el día en que se selló el manómetro. La diferencia de presión viene dada por:

\[\begin{aligned} P_{1}=P_{0}+\rho gh \end{aligned}\]

si definimos\(h\) ser positivos cuando el lado con la presión\(P_{0}\) es mayor (así\(h\) es negativo en la Figura\(\PageIndex{10}\) y\(P_{1}\) es menor que\(P_{0}\)).

También podemos medir la presión atmosférica absoluta si evacuamos el aire del extremo sellado del tubo, así que eso\(P_{0} = 0\). Al hacerlo, la diferencia de altura entre el fluido a ambos lados del manómetro es una medida de la presión atmosférica absoluta.

Ejemplo\(\PageIndex{3}\)

Figura\(\PageIndex{11}\): Barómetro construido a partir de un mamómetro para medir la presión atmosférica absoluta.

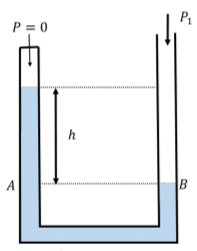
Usando un manómetro lleno de agua (\(ρ = 1 × 10^{3} \text{kg/m}^{3}\)), se construye un barómetro para medir la presión atmosférica absoluta evacuando el aire de un lado del manómetro, como se muestra en la Figura\(\PageIndex{11}\). ¿Cuál es la diferencia en altura\(h\),, cuando la presión atmosférica es “nominal”,\(P_{1} = 1.013 × 10^{5}\text{Pa}\)?

Solución:

La presión,\(P_{1}\), en el lado abierto del manómetro viene dada por:

\[\begin{aligned} P_{B} &=P_{A} \\ P_{1}&=P_{0}+\rho gh = \rho gh \end{aligned}\]

si el lado sellado del manómetro tiene una presión,\(P_{0} = 0\), por encima del fluido. Si\(P_{1} = 1.013 × 10^{5}\text{ Pa}\), podemos encontrar la altura,\(h\):

\[\begin{aligned} h=\frac{P_{1}}{\rho g}=\frac{(1.013\times 10^{5}\text{Pa})}{(1000\text{kg/m}^{3})(9.8\text{m/s}^{2})}=10.3\text{m} \end{aligned}\]

Discusión:

La diferencia de altura es aproximadamente\(10\text{ m}\) cuando la presión atmosférica es nominal. Esto significa que el manómetro necesita ser al menos así de alto para medir la presión atmosférica absoluta, ¡lo cual no es práctico de construir! Si, en cambio, se usa un líquido con una densidad mayor que la del agua, entonces esta altura se puede reducir sustancialmente. Tradicionalmente, los barómetros se han construido utilizando mercurio, que tiene una densidad de (\(ρ_{Hg} = 13.6 × 10^{3}\text{kg/m}^{3}\)), de manera que la diferencia de altura a presión atmosférica nominal es\(760\text{ mm}\). Este es un instrumento mucho más fácil de construir (aparte de las preocupaciones de seguridad del uso de mercurio). Por esta razón, una unidad de presión de uso frecuente es “mm de mercurio”, lo que corresponde a la diferencia de altura en un manómetro que se construye con mercurio.

Ejercicio\(\PageIndex{4}\)

Figura\(\PageIndex{12}\): Barómetro Torricelli.

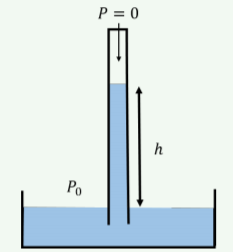
Se construye un barómetro Torricelli, como se ilustra en la Figura\(\PageIndex{12}\), para medir la presión atmosférica absoluta. El tubo vertical sellado tiene un espacio en la parte superior que se evacua (una presión de cero), de manera que la presión atmosférica sobre el recipiente de líquido fuerza al líquido subir el tubo a una altura\(h\), que es proporcional a la presión atmosférica. Si usas aceite de oliva como líquido, ¿qué puedes decir de la altura,\(h\), para la presión atmosférica nominal?

1. Es mayor que\(10.3\text{ m}\).
2. Es igual a\(10.3\text{ m}\).
3. Es menor que\(10.3\text{ m}\).
4. No hay suficiente información para contar.

Contestar

Notas al pie

1. Colocamos el\(dP\) en la parte superior del fluido, aunque la presión sea mayor en la parte inferior del fluido, debido a que el\(y\) eje aumenta hacia arriba. Estamos realmente interesados en el cambio de presión,\(dP\), que corresponde a un cambio de altura,\(dy\), a lo largo de la\(y\) dirección positiva.