17.2: Ley de Gauss

La Ley de Gauss es una relación entre el flujo neto a través de una superficie cerrada y la cantidad de carga,\(Q^{enc}\), en el volumen encerrado por esa superficie:

\[\oint\vec E\cdot d\vec A=\frac{Q^{enc}}{\epsilon_{0}}\]

En particular, tenga en cuenta que la Ley de Gauss es válida para cualquier superficie cerrada, y la forma de esa superficie no está especificada en la Ley de Gauss. Es decir, siempre podemos elegir la superficie a usar a la hora de calcular el flujo. Por razones obvias, a menudo llamamos a la superficie que elegimos una “superficie gaussiana”. Pero nuevamente, esta superficie es simplemente una herramienta matemática, no hay ninguna propiedad real que haga que una superficie sea “gaussiana”; simplemente significa que elegimos esa superficie para aplicar la Ley de Gauss. En el Ejemplo 17.1.3 anterior, confirmamos que la Ley de Gauss es compatible con la Ley de Coulomb para el caso de una carga puntual y una superficie gaussiana esférica.

Físicamente, la Ley de Gauss es una declaración de que las líneas de campo deben comenzar o terminar con una carga (las líneas de campo eléctrico se originan en cargas positivas y terminan con cargas negativas). Recordemos, el flujo es una medida del número neto de líneas que salen de una superficie. Si hay un número neto de líneas que salen de una superficie cerrada (un flujo positivo), esa superficie debe encerrar una carga positiva desde donde se originan esas líneas de campo. Del mismo modo, si hay el mismo número de líneas de campo entrando en una superficie cerrada que hay líneas que salen de esa superficie (un flujo de cero), entonces la superficie no encierra carga alguna. La Ley de Gauss simplemente establece que el número de líneas de campo que salen de una superficie cerrada es proporcional a la cantidad de carga encerrada por esa superficie.

Principalmente, la Ley de Gauss es una herramienta útil para determinar la magnitud del campo eléctrico a partir de una carga determinada, o distribución de carga. Por lo general, tenemos que utilizar la simetría para determinar la dirección del vector de campo eléctrico. En general, la integral para el flujo es difícil de evaluar, y la Ley de Gauss solo puede ser utilizada analíticamente en casos con un alto grado de simetría. Específicamente, la integral para el fundente es más fácil de evaluar si:

1. El campo eléctrico hace un ángulo constante con la superficie. Cuando este es el caso, el producto escalar puede escribirse en términos del coseno del ángulo entre\(\vec E\) y\(d\vec A\), que se puede sacar de la integral si es constante:\[\begin{aligned} \oint \vec E\cdot d\vec A=\oint E\cos\theta dA=\cos\theta\oint EdA\end{aligned}\] Idealmente, se ha elegido una superficie tal que este ángulo sea\(0\) o \(180^{\circ}\).
2. El campo eléctrico es constante en magnitud a lo largo de la superficie. Cuando este es el caso, la integral puede simplificarse aún más factorizando\(E\), y simplemente se convierte en una integral sobre\(dA\) (que corresponde al área total de la superficie,\(A\)):\[\begin{aligned} \oint \vec E\cdot d\vec A=\cos\theta\oint EdA =E\cos\theta\oint dA=EA\cos\theta \end{aligned}\]

En última instancia, los puntos anteriores deben dictar la elección de la superficie gaussiana para que la integral para el flujo sea fácil de evaluar. La elección de la superficie dependerá de la simetría del problema. Para una carga puntual (o esférica), una superficie gaussiana esférica permite calcular fácilmente el flujo (Ejemplo 17.1.3). Para una línea de carga, como veremos, un resultado de superficie cilíndrica es una buena opción para la superficie gaussiana. En términos generales, los pasos para aplicar la Ley de Gauss para determinar el campo eléctrico son los siguientes:

1. Hacer un diagrama que muestre la distribución de carga.
2. Utilice argumentos de simetría para determinar de qué manera apunta el vector de campo eléctrico.
3. Elija una superficie gaussiana que pase por el punto para el que desea conocer el campo eléctrico. Idealmente, la superficie es tal que el campo eléctrico es constante en magnitud y siempre hace el mismo ángulo con la superficie, de manera que la integral de flujo es sencilla de evaluar.
4. Calcular el flujo,\(\oint \vec E\cdot d\vec A\).
5. Calcular la cantidad de carga ubicada dentro del volumen encerrado por la superficie,\(Q^{enc}\).
6. Aplicar Ley de Gauss,\(\oint \vec E\cdot d\vec A=\frac{Q^{enc}}{\epsilon_0}\).

Ejemplo\(\PageIndex{1}\)

Una esfera aislante de radio,\(R\), contains a total charge, \(Q\), which is uniformly distributed throughout its volume. Determine an expression for the electric field as a function of distance, \(r\), from the center of the sphere.

Solución:

Obsérvese que esto es idéntico, matemáticamente, a la derivación que se hizo en la Sección 9.2 para el caso de gravedad.

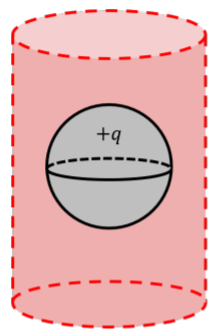
Al aplicar la Ley de Gauss, primero debemos pensar en la simetría para determinar la dirección del vector del campo eléctrico. También necesitamos pensar en todas las regiones posibles del espacio en las que necesitamos determinar el campo eléctrico. En particular, para este caso, necesitamos determinar el campo eléctrico tanto dentro (\(r\leq R\)) como fuera (\(r\geq R\)) de la esfera cargada.

La figura\(\PageIndex{1}\) muestra la esfera cargada de radio\(R\). Si consideramos la dirección del campo eléctrico fuera de la esfera (donde\(\vec E_{out}\) se dibuja), nos damos cuenta de que solo puede apuntar en la dirección radial (hacia o lejos del centro de la esfera), ya que esta es la única opción que preserva la simetría de la esfera. Al ser una esfera, la carga se ve igual desde todos los ángulos; así, el campo eléctrico también debe verse igual desde todos los ángulos, de lo contrario, habría una orientación preferida para la esfera. El mismo argumento se mantiene para el vector de campo eléctrico dentro de la esfera (dibujado como\(\vec E_{in}\)).

Figura\(\PageIndex{1}\): Para una distribución de carga esférica, el campo eléctrico interior y exterior debe apuntar n la dirección radical, por simetría.

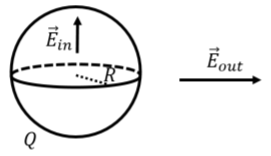
Ahora tenemos que elegir una superficie gaussiana que haga que el flujo integral sea fácil de evaluar. Idealmente, podemos encontrar una superficie sobre la cual el campo eléctrico forme el mismo ángulo con la superficie y sobre la cual el campo eléctrico sea de magnitud constante. Nuevamente, con base en la simetría de la distribución de carga, es evidente que una superficie esférica de radio\(r\),, satisfará estas propiedades.

Comenzamos aplicando la Ley de Gauss fuera de la carga (con\(r\geq R\)) para determinar el campo eléctrico,\(\vec E_{out}\). La figura\(\PageIndex{2}\) muestra nuestra elección de superficie gaussiana esférica (etiquetada\(S\)) de radio\(r\), que es concéntrica con la distribución de carga esférica del radio\(R\), y la carga total,\(+Q\).

Figura\(\PageIndex{2}\): Una superficie gaussiana esférica para determinar el campo eléctrico fuera de una esfera de radio, R, carga de retención,\(+Q\).

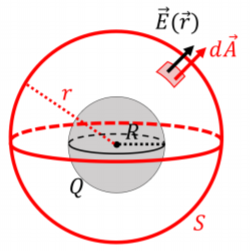
Para aplicar la Ley de Gauss, necesitamos calcular:

• el flujo neto a través de la superficie.
• la carga en el volumen encerrado por la superficie.

El flujo neto a través de la superficie se encuentra de la misma manera que en el Ejemplo 17.1.3, y viene dado por:\[\begin{aligned} \Phi_E&=\oint \vec E\cdot d\vec A=\oint E dA= E\oint dA=E(4\pi r^2)\end{aligned}\] donde nuestra elección de superficie esférica condujo a\(\vec E\cdot d\vec A=EdA\), ya que\(\vec E\) y\(d\vec A\) son siempre paralelos. Además, por simetría, el campo eléctrico debe ser constante en magnitud a lo largo de toda la superficie, o la simetría esférica se rompería. Esto nos permitió factorizar la\(E\) salida de la integral, dejándonos con,\(\oint dA\), que es simplemente el área de nuestra superficie esférica gaussiana,\(4\pi r^2\).

La superficie gaussiana con\(r\geq R\) encierra toda la esfera cargada, por lo que la carga encerrada es simplemente la carga de la esfera,\(Q^{enc}=Q\). La aplicación de la Ley de Gauss nos permite determinar la magnitud del campo eléctrico:\[\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\ E(4\pi r^2) &= \frac{Q}{\epsilon_0}\\ \therefore E&= \frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}\end{aligned}\] que es lo mismo que el campo eléctrico a una\(r\) distancia de una carga puntual. Así, desde el exterior, una distribución esférica de carga conduce al mismo campo eléctrico que si la carga estuviera concentrada en el centro de la esfera.

A continuación, determinamos la magnitud del campo eléctrico dentro de la esfera cargada. En este caso, elegimos una superficie gaussiana esférica de radio\(r\leq R\), que sea concéntrica con la esfera, como lo ilustra la superficie etiquetada,\(S\), que se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Una superficie gaussiana esférica para determinar el campo eléctrico dentro de una esfera de radio,\(R\), sosteniendo carga,\(+Q\).

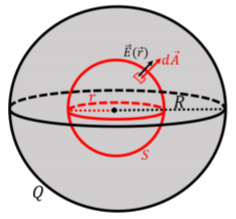
La integral de flujo vuelve a ser trivial, ya que el campo eléctrico siempre forma el mismo ángulo con la superficie gaussiana, y la magnitud del campo eléctrico es constante en magnitud a lo largo de la superficie:

\[\begin{aligned} \Phi_E&=\oint \vec E\cdot d\vec A=\oint E dA= E\oint dA=E(4\pi r^2)\end{aligned}\]

En este caso, sin embargo, la carga en el volumen encerrado por la superficie gaussiana es menor que\(Q\), ya que toda la carga no está encerrada. Se nos dice que la carga se distribuye uniformemente a lo largo del volumen esférico de radio\(R\). Podemos definir así una densidad de carga volumétrica,\(\rho\), (carga por unidad de volumen) para la esfera:

\[\begin{aligned} \rho=\frac{Q}{V}=\frac{Q}{\frac{4}{3}\pi R^3}\end{aligned}\]

El volumen encerrado por la superficie gaussiana es\(\frac{4}{3}\pi r^3\), así, la carga\(Q^{enc}\),, contenida en ese volumen viene dada por:

\[\begin{aligned} Q^{enc}=\frac{4}{3}\pi r^3 \rho=\frac{4}{3}\pi r^3 \frac{Q}{\frac{4}{3}\pi R^3}=Q\frac{r^3}{R^3}\end{aligned}\]

Finalmente, aplicamos la Ley de Gauss para encontrar la magnitud del campo eléctrico dentro de la esfera:

\[\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\ E(4\pi r^2) &=\frac{Q}{\epsilon_0}\frac{r^3}{R^3}\\ \therefore E&= \frac{Q}{4\pi\epsilon_0R^3}r\end{aligned}\]

Tenga en cuenta que el campo eléctrico aumenta linealmente con el radio dentro de la esfera cargada, y luego disminuye con el radio cuadrado fuera de la esfera. También, tenga en cuenta que en el centro de la esfera, el campo eléctrico tiene una magnitud de cero, como se esperaba de la simetría.

Discusión:

En este ejemplo, mostramos cómo usar la Ley de Gauss para determinar el campo eléctrico dentro y fuera de una esfera con carga uniforme. Reconocimos la simetría esférica de la distribución de carga y optamos por utilizar una superficie esférica para aplicar la Ley de Gauss. Esto, a su vez, permitió calcular fácilmente el flujo. Encontramos que fuera de la esfera, el campo eléctrico disminuye en magnitud con el radio al cuadrado, como si toda la carga estuviera concentrada en el centro de la esfera. Dentro de la esfera, encontramos que el campo eléctrico es cero en el centro, y aumenta linealmente con el radio.

Ejercicio\(\PageIndex{1}\)

Un caparazón esférico cargado delgado lleva una carga uniformemente distribuida de\(+Q\).

Figura\(\PageIndex{4}\): Una concha esférica cargada con un dispositivo cúbico en su interior.

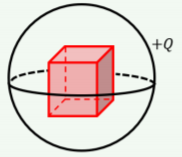
Si colocamos un cubo dentro del caparazón, como se muestra en la Figura\(\PageIndex{4}\), ¿cuál es el flujo total que sale de la superficie del cubo?

1. \(\frac{Q}{12\pi}\text{Vm}\).
2. \(\frac{Q}{2\pi}\text{Vm}\).
3. \(\frac{Q}{6}\text{Vm}\).
4. \(0\text{Vm}\).

Responder

Ejemplo\(\PageIndex{2}\)

Un cable recto infinitamente largo lleva una carga uniforme por unidad de longitud,\(\lambda\). What is the electric field at a distance, \(R\), from the wire?

Solución:

Comenzamos haciendo un diagrama de la distribución de carga, como en la Figura\(\PageIndex{5}\), para que podamos usar argumentos de simetría para determinar la dirección del vector de campo eléctrico. El vector de campo eléctrico podría ser:

1. en la dirección radial (punto a/desde el centro del cable).
2. tal que las líneas de campo eléctrico forman círculos concéntricos con el alambre.
3. colineal con el alambre.

En las tres posibilidades anteriores, no se podría inferir que se prefiere una dirección particular en el plano perpendicular al alambre. Las tres posibilidades preservan la simetría rotacional del cable (el alambre se ve igual desde todas las direcciones en el plano perpendicular al cable).

La segunda y tercera opciones se pueden eliminar, porque esperamos que las líneas de campo eléctrico tengan al menos un componente radial, ya que esperamos que una carga negativa sea atraída por el cable. El campo eléctrico se verá así como el ilustrado en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): Una línea infinita de carga que transporta carga uniforme por unidad de longitud,\(λ\). El panel izquierdo muestra una vista lateral y el panel derecho una vista desde arriba. El campo eléctrico debe estar en la dirección radial o habría una dirección preferida.

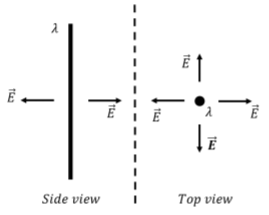
A continuación, tenemos que elegir una superficie gaussiana para aplicar la Ley de Gauss. Una opción conveniente es un cilindro (un “pastillero”) de radio,\(R\), y longitud\(L\), como se muestra en la Figura\(\PageIndex{6}\), ya que éste pasa por un punto que está a una distancia\(R\),, del cable (donde se nos pide el campo eléctrico). En todos los puntos de la superficie cilíndrica, el vector de campo eléctrico es perpendicular o paralelo a la superficie.

Figura\(\PageIndex{6}\): Se utiliza una superficie gaussiana cilíndrica para calcular el flujo a partir de una línea infinita de carga.

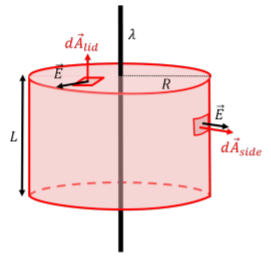
Podemos pensar en la superficie cilíndrica como compuesta por tres superficies: 2 discos en cada extremo (las tapas del pastillero), y la superficie curva que conforma el costado del cilindro. El flujo a través de toda la superficie cilíndrica será la suma de los flujos a través de las dos tapas más el flujo a través del lado:\[\begin{aligned} \oint \vec E\cdot d\vec A = \int_{side} \vec E\cdot d\vec A + \int_{lid}\vec E\cdot d\vec A + \int_{lid}\vec E\cdot d\vec A\end{aligned}\] donde hay que señalar que la integral cerrada (\(\oint\)) se separó en tres integrales normales (\(\int\)) correspondientes a las tres” superficies abiertas” que conforman la superficie cerrada. Nuevamente, recuerde que el flujo es proporcional al número neto de líneas de campo que salen/ingresan a la superficie cerrada, por lo que tiene sentido contar esas líneas sobre las tres superficies abiertas y sumarlas juntas para obtener el número total de la superficie cerrada.

El flujo a través de las tapas es idéntico cero, ya que el campo eléctrico es perpendicular a\(d\vec A\) todas partes en las tapas. El flujo total es así igual al flujo a través de la superficie lateral curvada, para lo cual el vector de campo eléctrico es siempre paralelo a\(d\vec A\), y para el cual el vector de campo eléctrico es constante en magnitud:\[\begin{aligned} \oint \vec E\cdot d\vec A = \int_{side} \vec E\cdot d\vec A =\int_{side} EdA=E\int_{side}dA=E(2\pi R L)\end{aligned}\] donde reconocimos que la superficie lateral puede desplegarse en un rectángulo de altura,\(L\), y anchura,\(2\pi R\), correspondientes a la circunferencia del cilindro, de manera que el área del lado del cilindro viene dada por\(A=2\pi R L\).

A continuación, determinamos la carga dentro del volumen encerrado por la superficie. Dado que el cilindro encierra una longitud,\(L\), de alambre, la carga encerrada viene dada por:\[\begin{aligned} Q^{enc}=\lambda L\end{aligned}\] donde\(\lambda\) está la carga por unidad de longitud en el cable. Poner esto en conjunto en la Ley de Gauss nos da el campo eléctrico a una distancia,\(R\), del cable:\[\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\ E(2\pi R L) &= \frac{\lambda L}{\epsilon_0}\\ \therefore E&= \frac{\lambda}{2\pi\epsilon_0R}\end{aligned}\] Obsérvese que este es el mismo resultado que obtuvimos en el Ejemplo 16.3.3 cuando tomamos el límite de la línea finita de carga que tiene longitud infinita.

Discusión:

En este ejemplo, aplicamos la Ley de Gauss para determinar el campo eléctrico a una distancia de un cable cargado infinitamente largo. Utilizamos la simetría para argumentar que el campo debe ser radial y en el plano perpendicular al alambre, y reconocimos que una superficie gaussiana cilíndrica explotaría la simetría para que el flujo pueda calcularse fácilmente. Obtuvimos el mismo resultado que al integrar la Ley de Coulomb en el Ejemplo 16.3.3. Sin embargo, usar la Ley de Gauss fue mucho menos trabajo que integrar la Ley de Coulomb.

Ejercicio\(\PageIndex{2}\)

¿Por qué es difícil aplicar la Ley de Gauss a un alambre finito?

1. Es fácil aplicar la Ley de Gauss a un alambre finito.
2. Porque el flujo de un cable finito es indefinido.
3. Porque no conocemos la densidad de carga de un cable finito.
4. Porque el argumento de simetría no se sostiene.

Responder

Pensamientos de josh

La Ley de Gauss nos obliga a elegir una superficie “gaussiana”, pero ¿qué superficie debemos elegir? Generalmente, es útil elegir una superficie de tal manera que el flujo pueda determinarse fácilmente, idealmente sin tener que hacer realmente una integral. Si la simetría puede ser explotada de tal manera que\(\vec E\) tiene una magnitud constante y dirección relativa\(d\vec A\) a en cada ubicación de la superficie gaussiana, entonces\(\int \vec E \cdot d\vec A\) será igual a\(E A\). Es por ello que las superficies gaussianas suelen tener la misma forma que el objeto cargado que encierran.

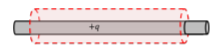
Por ejemplo, si necesito encerrar una carga cilíndrica, sería razonable encerrar la carga con una superficie gaussiana cilíndrica, como se muestra en la Figura\(\PageIndex{7}\)

Figura\(\PageIndex{7}\): Una superficie gaussiana cilíndrica para encerrar una carga cilíndrica.

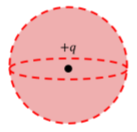
Cuando se trata de cargas puntuales que no tienen forma y por lo tanto son esféricamente simétricas, tiene sentido elegir una superficie gaussiana esférica, como se muestra en la Figura\(\PageIndex{8}\), ya que el campo eléctrico está en la dirección radial para una carga puntual.

Figura\(\PageIndex{8}\): Una superficie gaussiana esférica para encerrar una carga puntual.

Finalmente, hay algunos casos de opciones menos que ideales para las superficies gaussianas. Si bien nunca se equivocan, pueden requerir integrales bastante complicadas para determinar el flujo. Estos casos seguirán proporcionando una respuesta correcta si la situación se modela correctamente.

Supongamos que encierro una carga esférica con una superficie gaussiana cilíndrica, como se muestra en la Figura\(\PageIndex{9}\). El campo eléctrico será más fuerte cerca de la mitad de la longitud del cilindro que en el centro de sus tapas finales, lo que significa que no\(\vec E\) es constante en\(\int \vec E \cdot d \vec A\), por lo que la integral no se puede simplificar a\(EA\). Una mejor opción para una superficie gaussiana en este caso sería una esfera, que explota la simetría de la distribución de carga y proporciona resultados en una magnitud constante en todas partes a lo largo\(\vec E\) de la superficie. Las figuras 17.2.7 y 17.2.8 dan otros ejemplos de cuando no podemos asumir que\(\Phi\) somos iguales a\(EA\).

Figura\(\PageIndex{9}\): Una superficie cilíndrica no es una buena opción para encerrar una carga esférica.

Ejemplo\(\PageIndex{3}\)

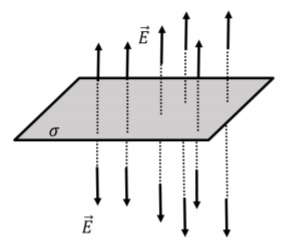
Determinar el campo eléctrico sobre un plano de carga infinitamente grande con carga superficial uniforme por unidad de área,\(\sigma\).

Solución:

La figura\(\PageIndex{10}\) muestra una porción del plano infinito. El vector de campo eléctrico debe ser perpendicular al plano o una dirección preferida podría inferirse de otra manera a partir de la dirección del campo eléctrico. También podemos argumentar que los componentes horizontales del campo eléctrico se cancelarán en todas partes por encima del plano, ya que el plano es infinito. El campo eléctrico apuntará lejos de (hacia) el avión, si la carga es positiva (negativa).

Figura\(\PageIndex{10}\): El campo eléctrico por encima de un plano infinito con carga uniforme por unidad de área\(σ\),, debe ser perpendicular al plano.

Una superficie gaussiana cilíndrica o en forma de caja conduciría tanto a que la integral de flujo fuera fácil de calcular, como se ilustra en la Figura\(\PageIndex{11}\). En efecto, dado que el campo eléctrico es perpendicular al plano, sólo las partes de la superficie que son paralelas al plano (las tapas en el cilindro, los dos planos horizontales en la caja) tendrán un flujo neto a través de ellos.

Figura\(\PageIndex{11}\): Una superficie cilíndrica o una caja son buenas opciones para una superficie gaussiana por encima de un plano, ya que solo las partes de la superficie paralelas al plano tendrán flujo neto a través de ellas.

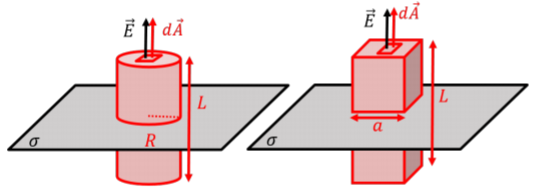
Escojamos una caja (panel derecho de la Figura\(\PageIndex{11}\)) de longitud,\(L\), con una sección transversal cuadrada de lado,\(a\). Colocamos la caja de tal manera que el avión intersecta el centro de la caja (aunque esto no es obligatorio, ya que ya sabemos que el campo eléctrico no dependerá de la distancia del avión). El flujo a través de la caja es simplemente el flujo a través de los dos planos horizontales (de área\(a^2\)):\[\begin{aligned} \oint \vec E\cdot d\vec A&= \int_{top} EdA+\int_{bottom}EdA=2Ea^2\end{aligned}\] La caja encierra una sección del plano con área\(a^2\), de manera que la carga neta encerrada por la superficie es:\[\begin{aligned} Q^{enc}=\sigma a^2\end{aligned}\] Aplicar la Ley de Gauss nos permite determinar la magnitud del campo eléctrico:\[\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0} \\ 2Ea^2&= \frac{\sigma a^2}{\epsilon_0}\\ \therefore E&= \frac{\sigma}{2\epsilon_0}\end{aligned}\] que es el mismo resultado que encontramos en el Ejemplo 16.3.4.

Discusión:

En este ejemplo, utilizamos la Ley de Gauss para determinar el campo eléctrico por encima de un plano infinito. Encontramos que teníamos una opción de superficies gaussianas (cilindro, caja) que nos permitieron aplicar la Ley de Gauss. Encontramos el mismo resultado que habíamos encontrado en el Ejemplo 16.3.4 donde habíamos integrado la Ley de Coulomb (dos veces, una para un anillo de carga, luego para un disco, luego tomó el límite del radio del disco yendo al infinito). Nuevamente, vemos que en configuraciones con una simetría de alto grado, la Ley de Gauss puede ser muy sencilla de aplicar.