17.7: Problemas y soluciones de la muestra

Ejercicio\(\PageIndex{1}\)

Considere una esfera cargada de radio,\(R\), which has a non-uniform charge density, that varies with radius, as \(\rho(r) = ar^2\).

1. ¿Cuál es la carga total sobre la esfera?
2. ¿Cuál es el campo eléctrico en función de la distancia desde el centro de la esfera fuera de la esfera,\(r>R\)?
3. ¿Cuál es el campo eléctrico en función de la distancia desde el centro de la esfera dentro de la esfera,\(r\leq R\)?

Contestar

a. para determinar la carga total de la esfera, dividimos la esfera en conchas infinitesimales de radio\(r\), y grosor,\(dr\). El volumen,\(dV\), de una de estas conchas infinitesimales es su área (dada por el área de la superficie de una esfera de radio\(r\)), multiplicada por su espesor,\(dr\):\[\begin{aligned} dV = 4\pi r^2 dr\end{aligned}\] La carga,\(dQ\), de una de esas conchas viene dada por la carga por unidad de volumen,\(\rho(r)\):\[\begin{aligned} dQ = \rho(r) dV = ar^24\pi r^2 dr = 4a\pi r^4 dr\end{aligned}\] La carga total de la esfera se encuentra sumando la carga de cada proyectil:\[\begin{aligned} Q=\int dQ =\int_0^R4a\pi r^4 dr=\frac{4}{5}a\pi R^5\end{aligned}\]

b. Fuera de la esfera, podemos usar una superficie gaussiana esférica de radio\(r\), de manera que el flujo viene dado por: Toda\[\begin{aligned} \oint \vec E\cdot d\vec A=4\pi r^2 E\end{aligned}\] la carga de la esfera está encerrada. Aplicando la Ley de Gauss, podemos determinar el campo eléctrico fuera de la esfera:\[\begin{aligned} \oint \vec E\cdot d\vec A&= \frac{Q^{enc}}{\epsilon_0}\\ 4\pi r^2 E&= \frac{4a\pi R^5}{5\epsilon_0}\\ \therefore E(r)&=\frac{aR^5}{5\epsilon_0r^2}\end{aligned}\] y vemos que el campo eléctrico disminuye a medida que el radio se cuadra, lo cual tiene sentido, ya que desde fuera de la esfera, no sabemos cómo se distribuye la carga en su interior.

c. Dentro del volumen de la esfera, todavía utilizamos una superficie esférica gaussiana de radio,\(r\), de manera que el flujo viene dado por:\[\begin{aligned} \oint \vec E\cdot d\vec A=4\pi r^2 E\end{aligned}\] Sin embargo, dentro de la esfera, la superficie gaussiana solo encierra la carga hasta un radio de\(r\), que encontramos por integración, similar a parte a):\[\begin{aligned} Q^{enc}=\int dQ =\int_0^r 4a\pi r^4 dr=\frac{4}{5}a\pi r^5\end{aligned}\] Aplicando la Ley de Gauss:\[\begin{aligned} \oint \vec E\cdot d\vec A&= \frac{Q^{enc}}{\epsilon_0}\\ 4\pi r^2 E&= \frac{4a\pi r^5}{5\epsilon_0}\\ \therefore E(r)&=\frac{ar^3}{5\epsilon_0r^2}\end{aligned}\] y encontramos que el campo eléctrico es cero en el centro de la esfera y aumenta con el radio cubo dentro de la esfera.

Ejercicio\(\PageIndex{2}\)

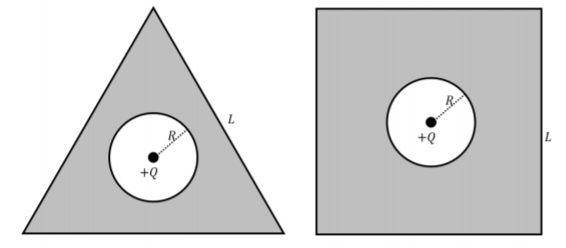
C onsider dos placas conductoras que se ilustran en la Figura\(\PageIndex{1}\). Both plates have a hollow circle of radius, \(R\), at their center. One plate is a square on the outside and the other is a triangle on the outside, both of the outside shapes have a side length of \(L\). A point charge of charge \(+Q\) is placed at the center of the hollowed out circle of both plates.

1. ¿Cuál es el campo eléctrico fuera de las conchas?
2. ¿Cuál es la densidad de carga lineal promedio en las superficies interna y externa de los proyectiles?
3. ¿Qué secciones de las dos placas tendrían la mayor densidad de carga?

Figura\(\PageIndex{1}\): Una concha triangular y cuadrada, ambas con un centro circular ahuecado y una carga puntual.

Contestar

a. Los proyectiles conductores no tienen carga neta, por lo que la única carga en el sistema es la carga puntual\(Q\). Si dibujamos una superficie gaussiana esférica, la única carga encerrada será\(Q\), y podemos ignorar las cargas en las placas. El campo eléctrico es así el campo de una carga puntual:\[\begin{aligned} E= \frac{kQ}{r^2} \end{aligned}\]

b. comencemos con el caparazón que tiene un triángulo en el exterior. Utilizaremos la ley de Gauss para determinar la densidad de carga de las conchas internas y externas. Para ello, dibujaremos un círculo dentro del caparazón,\(S_1\) y un triángulo fuera del caparazón exterior,\(S_2\) como se muestra en la Figura\(\PageIndex{2}\).

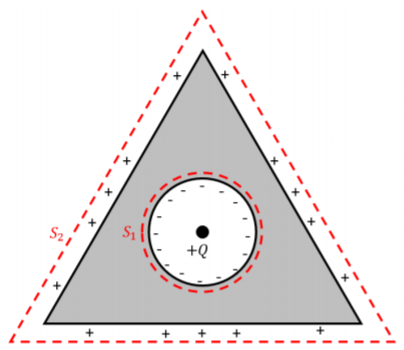
Figura\(\PageIndex{2}\): Una solución al caparazón conductor triangular.

Al considerar\(S_1\), sabemos que el campo eléctrico dentro de la carcasa (conductora) es\(0\), por lo que el flujo de salida\(S_1\) será cero. Esto significa que la carga puntual en el interior del proyectil será igual y opuesta a la suma de las cargas superficiales en el caparazón interior. A partir de aquí, dividimos la carga neta por la circunferencia de la concha interna para determinar la densidad de carga lineal:\[\begin{aligned} \lambda_{circle} = \frac{-Q}{2\pi R} \end{aligned}\] Al considerar\(S_2\), sabemos que la\(Q_{enc} = +Q\), lo que significa que la carga lineal total en el triángulo exterior será\(+Q\) tal que cancela el\(-Q\) a lo largo del círculo interno. La suma de los cargos sería\(Q_{enc} = Q_{point}+Q_{triangle}-Q_{circle}\). Sabiendo esto, debemos dividir la carga total en la superficie exterior por la suma de la longitud de cada uno de los lados del triángulo para encontrar la densidad de carga lineal promedio:\[\begin{aligned} \lambda_{circle} = \frac{Q}{3L} \end{aligned}\] Ahora, consideramos las densidades de carga lineal interna y externa de la concha conductora cuadrada. Elegimos dos superficies gaussianas,\(S_1\), y\(S_2\), como se muestra en la Figura\(\PageIndex{3}\):

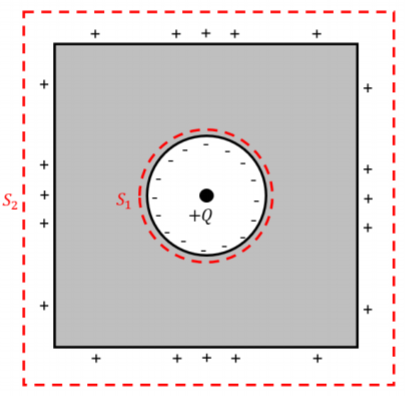
Figura\(\PageIndex{3}\): Una solución a la carcasa conductora cuadrada.

Porque\(S_1\), el círculo se trata como estaba mientras se resolvía la concha triangular. El campo eléctrico también se\(0\) encuentra dentro de la carcasa conductora cuadrada, por lo que sabemos que la densidad de carga lineal promedio es\(\frac{-Q}{2\pi R}\).

Al considerar\(S_2\), sabemos que\(Q_{enc}\) es así\(+Q\), por lo que sabemos que la carga total sobre la superficie cuadrada del caparazón será\(+Q\). Esto nos deja con la siguiente densidad de carga lineal promedio:\[\begin{aligned} \lambda_{square} = \frac{Q}{4L} \end{aligned}\]

c. Estas placas son cargadas por el campo eléctrico generado por la carga puntual mantenida dentro de ellas, lo que significa que la densidad de carga lineal de las dos placas será mayor en los puntos a lo largo de los lados exteriores que están a la distancia más corta de la carga puntual. Estos puntos ocurren en las placas triangulares y cuadradas en el punto que es el más cercano a la carga\(Q\), como se muestra en la Figura\(\PageIndex{4}\).

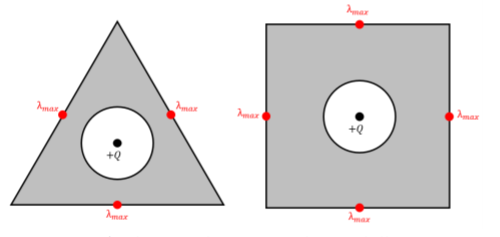
Figura\(\PageIndex{4}\): Una solución a la carcasa conductora cuadrada.