18.3: Cálculo del potencial eléctrico a partir de distribuciones de carga

En esta sección, damos dos ejemplos de determinación del potencial eléctrico para diferentes distribuciones de carga. Tenemos dos métodos que podemos utilizar para calcular el potencial eléctrico a partir de una distribución de cargas:

1. Modelar la distribución de carga como la suma de cargas puntuales infinitesimales\(dq\),, y sumar los potenciales eléctricos,\(dV\), de todas las cargas,\(dq\). Esto requiere que uno elija\(0\text{V}\) ubicarse en el infinito, de manera que los\(dV\) sean todos relativos al mismo punto.
2. Calcule el campo eléctrico (ya sea como integral o a partir de la Ley de Gauss), y use:\[\begin{aligned} \Delta V &=V(\vec r_B)-V(\vec r_A)=-\int_A^B \vec E\cdot d\vec r\end{aligned}\]

El primer método es similar a cómo calculamos el campo eléctrico para cargas distribuidas en el capítulo 16, pero con la simplificación de que solo necesitamos sumar escalares en lugar de vectores. El segundo método ya se introdujo en este capítulo.

Ejemplo\(\PageIndex{1}\)

Un anillo de radio\(R\) carries a total charge \(+Q\). Determine the electric potential a distance \(a\) from the center of the ring, along the axis of symmetry of the ring. Assume that zero electric potential is defined at infinity.

Solución:

La figura\(\PageIndex{1}\) muestra un diagrama del anillo, y nuestra elección de carga infinitesimal,\(dq\).

Figura\(\PageIndex{1}\): Determinar el potencial eléctrico en el eje de un anillo de radio\(R\) portador de carga\(Q\).

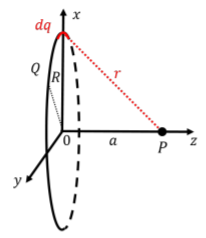
Para calcular el potencial eléctrico en el punto\(P\), con\(0\text{V}\) definido como en el infinito, primero calculamos el potencial infinitesimal a\(P\) partir de la carga puntual infinitesimal,\(dq\):\[\begin{aligned} dV=k\frac{dq}{r}\end{aligned}\] El potencial eléctrico total es entonces la suma (integral) de estos potenciales:\[\begin{aligned} V=\int dV=\int k\frac{dq}{r} = \frac{k}{r}\int dq=k\frac{Q}{r}=k\frac{Q}{\sqrt{a^2+R^2}}\end{aligned}\] donde reconocemos eso\(k\) y\(r\) son los mismos para cada uno\(dq\), para que puedan facturar fuera de la integral. \(\int dq=Q\)es entonces solo la suma de las cargas infinitesimales, que deben sumarse a la carga del anillo.

Discusión:

En este ejemplo, determinamos el potencial eléctrico, relativo al infinito, a una distancia\(a\) desde el centro de un anillo de carga, a lo largo de su eje de simetría. Modelamos el anillo como hecho de muchas cargas puntuales infinitesimales, y sumamos los potenciales eléctricos infinitesimales de esas cargas relativas al infinito. Esto fue mucho más sencillo que determinar el campo eléctrico, ya que el potencial eléctrico es un escalar y no necesitamos considerar cómo cancelarán los componentes de diferentes\(dq\) a lo largo del anillo.

Ejemplo\(\PageIndex{2}\)

Un cable largo, delgado y recto lleva una carga uniforme por unidad de longitud,\(\lambda\). Se encuentra que la diferencia de potencial eléctrico entre los puntos ubicados a distancias\(r_B=2\text{cm}\) y\(r_A=1\text{cm}\) del cable es\(V(r_B)-V(r_A)=-100\text{V}\). ¿Cuál es la densidad de carga lineal en el alambre\(\lambda\)?

Figura\(\PageIndex{2}\): Un cable largo y delgado con mediciones de potencial eléctrico en diferentes puntos.

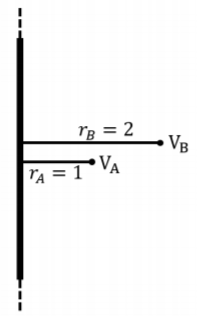
Solución:

En este caso, podemos usar la Ley de Gauss para determinar el campo eléctrico a cierta distancia del cable. A partir de eso, podemos calcular la diferencia de potencial eléctrico entre dos puntos cualesquiera cerca del cable, y así la densidad de carga en el cable.

Mediante el uso de una superficie cilíndrica de longitud\(L\),, y radio\(r\),, podemos usar la Ley de Gauss para determinar el campo a una distancia\(r\),, desde el cable:\[\begin{aligned} \oint \vec E\cdot d\vec A&=\frac{Q^{enc}}{\epsilon_0}\\ 2\pi r L E&= \frac{\lambda L}{\epsilon_0}\\ \therefore \vec E(r)&=\frac{\lambda}{2\pi\epsilon_0 r}\hat r\end{aligned}\] Usando el campo eléctrico, podemos calcular la diferencia de potencial entre dos puntos que están en distancias,\(r_A\) y\(r_B\), desde el cable:\[\begin{aligned} \Delta V &=V(r_B)-V(r_A)=-\int_{r_A}^{r_B} \vec E\cdot d\vec r\\ &=-\int_{r_A}^{r_B} \left( \frac{\lambda}{2\pi\epsilon_0 r}\hat r \right)\cdot d\vec r=-\frac{\lambda}{2\pi\epsilon_0}\int_{r_A}^{r_B} \frac{1}{r}\hat r \cdot d\vec r=-\frac{\lambda}{2\pi\epsilon_0}\int_{r_A}^{r_B} \frac{1}{r}dr\\ &=-\frac{\lambda}{2\pi\epsilon_0}\left[|\ln(r)|\right]_{r_A}^{r_B} = -\frac{\lambda}{2\pi\epsilon_0}\ln\left(\frac{r_B}{r_A}\right)\\ \therefore\Delta V &=\frac{\lambda}{2\pi\epsilon_0}\ln\left(\frac{r_A}{r_B}\right)\end{aligned}\] donde, en la segunda última línea, eliminamos el valor absoluto del logaritmo, ya que\(r_A<r_B\), y en la última línea, eliminamos el signo menos invirtiendo el argumento del logaritmo. Ya que conocemos la diferencia de potencial\(\Delta V\),, para dos puntos ubicados a distancias\(r_B=2\text{cm}\) y\(r_A=1\text{cm}\), podemos determinar la densidad de carga en el cable: ¡\[\begin{aligned} \Delta V &=V(r_B)-V(r_A)=-100\text{V}\\ \Delta V &=\frac{\lambda}{2\pi\epsilon_0}\ln\left(\frac{r_A}{r_B}\right)\\ \therefore \lambda &= \frac{2\pi\epsilon_0\Delta V}{\ln\left(\frac{r_A}{r_B}\right)}=\frac{2\pi(8.85\times 10^{-12}\text{C}^2\cdot \text{N}^{-1}\cdot \text{m}^{-2})(-100\text{V})}{\ln\left(\frac{1}{2}\right)}=8.02\times 10^{-9}\text{C/m}\end{aligned}\]donde, de nuevo, hay que tener mucho cuidado con las señales! Tenga en cuenta que también tiene sentido que la diferencia de potencial,\(\Delta V =V(r_B)-V(r_A)\), sea negativa, ya que\(r_A\) está más cerca del cable cargado positivamente. Una carga positiva en reposo se alejaría del cable cargado positivamente, de\(r_A\) a\(r_B\), de alto potencial a bajo potencial.

Discusión:

En este ejemplo, mostramos cómo determinar el potencial eléctrico cerca de un cable cargado infinitamente largo utilizando el campo eléctrico que determinamos a partir de la Ley de Gauss. Al conocer la diferencia de potencial entre dos puntos cerca del cable, pudimos inferir entonces la densidad de carga en el cable.