18.5: Capacitores

Los capacitores son dispositivos electrónicos comunes que se utilizan para almacenar carga eléctrica para una variedad de aplicaciones. Un condensador generalmente se construye con dos placas conductoras (llamadas “terminales” o “electrodos”) separadas por aire o un material aislante.

Figura\(\PageIndex{1}\): Dos ejemplos de capacitores. El panel izquierdo muestra un condensador de “placa paralela”, y el panel derecho muestra un condensador de forma cilíndrica obtenido al “enrollar” un condensador de placa paralela.

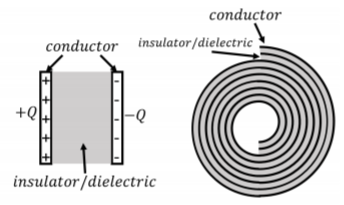
La figura\(\PageIndex{1}\) muestra dos ejemplos de capacitores. El panel izquierdo muestra un condensador de “placa paralela”, que consiste en dos placas conductoras separadas por aire o un aislante. Las placas son conductoras para que una pueda agregar y quitar fácilmente carga a las placas. Las placas siempre tienen cargas iguales y opuestas. El panel derecho muestra una implementación más práctica de un condensador que podría usarse en un circuito, el cual se realiza simplemente “enrollando” un condensador de placa paralela (con un aislante en lugar de aire que separa las placas para que no se toquen).

Capacitancia

Siempre y cuando las cantidades de carga involucradas no sean demasiado grandes, se ha observado que la cantidad de carga,\(Q\), que puede almacenarse en un condensador ¹, es linealmente proporcional a la diferencia de potencial,\(\Delta V\), entre las dos placas:

\[\begin{aligned} Q\propto \Delta V\end{aligned}\]

\[Q=C\Delta V\]

La constante de proporcionalidad\(C\), entre carga y diferencia de potencial a través del condensador (generalmente llamada voltaje a través del condensador) se llama “capacitancia”, y tiene unidades S.I. de “Faradios”,\(F\). La capacitancia de un condensador en particular es una medida de cuánta carga puede contener a un voltaje dado y depende de la geometría del condensador así como del material entre los terminales. Si se coloca demasiada carga en un condensador, el material entre las dos placas se descompondrá, y una chispa generalmente dañará el condensador así como lo descargará.

Podemos calcular fácilmente la capacitancia de un condensador de placa paralela. Modelamos el condensador como hecho de dos placas conductoras, cada una con área,\(A\), separadas por una distancia,\(L\), y manteniendo carga con magnitud,\(Q\). La densidad de carga superficial en una de las placas\(\sigma\),, viene dada por:\[\begin{aligned} \sigma =\frac{Q}{A}\end{aligned}\] En el Ejemplo 18.2.3, encontramos una expresión para la diferencia de potencial entre dos placas paralelas:\[\begin{aligned} \Delta V &= \frac{\sigma}{\epsilon_0}L=\left(\frac{L}{A\epsilon_0}\right)Q\end{aligned}\] Comparando con,\(Q=C\Delta V\), la capacitancia de la placa paralela se encuentra que el condensador es:\[\begin{aligned} C=\epsilon_0\frac{A}{L}\end{aligned}\] Tiene sentido que la capacitancia, la cantidad de carga que se puede almacenar a un voltaje dado, aumenta si las placas tienen un área mayor (más espacio para cargas), y disminuye si las placas están más separadas (campo eléctrico más pequeño).

Los capacitores se utilizan en muchas pantallas táctiles. Por ejemplo, estos podrían estar hechos de vidrio (un aislante), con una fina capa metálica que se toca para interactuar con la pantalla (una de las placas). Al tocar la placa de metal, cambia efectivamente la capacitancia de la pantalla, que se puede detectar y modelar para determinar la ubicación de su (s) dedo (s). La pantalla táctil moderna tiene muchos capacitores integrados directamente en la pantalla, y la función se basa en este principio.

Ejercicio\(\PageIndex{1}\)

Un condensador sostiene\(0.2\text{C}\) of charge when it has a potential difference of \(500\text{V}\) between its plates. If the same capacitor holds \(0.15\text{C}\) of charge, what is the potential difference between its plates?

1. \(375\text{ V}\).
2. \(500 \text{V}\).
3. \(75\text{ V}\).
4. \(150\text{ V}\).

Contestar

Materiales dieléctricos

En la práctica, los capacitores siempre tienen un material aislante entre las dos placas. El material se elige para tener un voltaje de ruptura más alto que el aire, de modo que se puedan almacenar más cargas antes de que ocurra una avería. También se ha observado experimentalmente que la capacitancia aumenta con ciertos materiales, los llamados “materiales dieléctricos”. Un material dieléctrico tiene una “constante dieléctrica”\(K\), definida como la cantidad en la que aumenta la capacitancia:\[\begin{aligned} C=KC_0\end{aligned}\] donde\(C\) está la capacitancia con el material en su lugar, y\(C_0\) es la capacitancia cuando hay vacío entre las placas ( la constante dieléctrica del aire es muy cercana a 1). A menudo, más que la constante dieléctrica, se utiliza la “permitividad”\(\epsilon\),, de un material:\[\begin{aligned} \epsilon=K\epsilon_0\end{aligned}\] basado en la permitividad del espacio libre,\(\epsilon_0\). La capacitancia de un condensador de placa paralela, con un material que tiene permitividad\(\epsilon\), viene dada por: Los materiales\[\begin{aligned} C=K\epsilon_0\frac{A}{L}=\epsilon\frac{A}{L}\end{aligned}\] dieléctricos están hechos de moléculas que pueden polarizarse (como agua), es decir, moléculas que tienen un momento dipolo eléctrico distinto de cero. Cuando el material dieléctrico se coloca entre las placas, los dipolos dentro del material se alinean con el campo eléctrico de las placas. Esto conduce a un segundo campo eléctrico, desde los dipolos, en la dirección opuesta del campo a las placas, reduciendo así el campo eléctrico total entre las placas. Esto, a su vez, permite que se mantengan más cargas en la placa para un voltaje dado. Esto se ilustra en la Figura\(\PageIndex{2}\)

Figura\(\PageIndex{2}\): Se coloca un material dieléctrico entre las dos placas de un condensador. Los dipolos eléctricos en el dieléctrico tienen orientaciones aleatorias cuando las placas son neutras (panel izquierdo). Cuando las placas están cargadas (panel derecho), los dipolos se alinean con el campo de las placas, permitiendo que haya más carga en las placas a una diferencia de potencial dada.

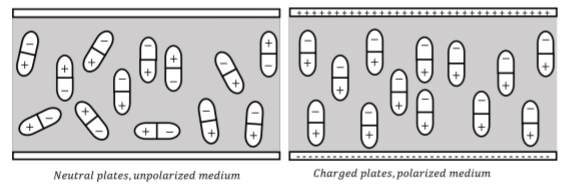
Nótese que, en un material dieléctrico con permitividad\(\epsilon\),, se modifica la Ley de Gauss para que diga:\[\begin{aligned} \oint \vec E\cdot d\vec A=\frac{Q^{enc}}{\epsilon}\end{aligned}\] donde la permitividad del espacio libre\(\epsilon_0\),, simplemente se sustituye por la permitividad del material,\(\epsilon\).

Energía almacenada en un condensador

Las cargas almacenadas en un condensador tienen energía potencial eléctrica: si uno colocara un conductor entre las placas, las cargas conducirían inmediatamente de una placa a la otra y ganarían energía cinética. Podemos modelar la cantidad de energía almacenada en el condensador considerando cuánto trabajo se necesita para colocar las cargas en el condensador.

Imagínese que ambas placas en el condensador arrancan con una carga de magnitud,\(q\). Luego retiramos una carga negativa infinitesimal, con magnitud\(dq\), de la placa positiva y la colocamos sobre la placa negativa. Esto requirió trabajo, ya que tuvimos que sacar esta carga negativa de la placa positiva. Si la diferencia de potencial a través de las placas es\(\Delta V\), entonces tuvimos que hacer una cantidad de trabajo dada por:\[\begin{aligned} dW = \Delta Vdq\end{aligned}\] ya que la carga ahora\(dq\) ha ganado energía potencial,\(\Delta Vdq\). Sin embargo, la diferencia de potencial depende de la capacitancia (constante) del condensador, y la cantidad de carga\(q\),, ya almacenada\[\begin{aligned} q &= C\Delta V\\ \therefore \Delta V&=\frac{q}{C}\end{aligned}\] en las placas: Para determinar el trabajo requerido para transferir una cantidad total de carga,\(Q\), sumamos el trabajo en transfiriendo cada carga infinitesimal,\(dq\):\[\begin{aligned} W=\int dW=\int_0^Q \Delta Vdq=\int_0^Q \frac{q}{C}dq=\frac{1}{2}\frac{Q^2}{C}\end{aligned}\] Así, la energía potencial total que se almacena en un condensador viene dada por:\[\begin{aligned} U = \frac{1}{2}\frac{Q^2}{C} = \frac{1}{2}Q(\Delta V)^2=\frac{1}{2}Q\Delta V\end{aligned}\] donde hicimos uso de\(Q=C\Delta V\) para mostrar la fórmula con diferentes elecciones de variables. En cualquier caso, la cantidad de energía que se almacena aumenta con la cantidad de carga, la capacitancia y el voltaje a través del condensador. Los capacitores son útiles porque esta energía se puede liberar rápidamente, como en el brillante destello de luz requerido para la fotografía con flash.

Notas al pie

1. Esta es la cantidad de carga en una de las placas. En su conjunto, el condensador es neutro.