20.3: Aplicando la regla de Kirchhoff a modelar circuitos

Última actualización
Guardar como PDF

Page ID: 128826

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, mostramos cómo modelar un circuito usando las reglas de Kirchhoff. En general, se puede considerar que un circuito se modele completamente si se puede determinar la corriente en cada segmento del circuito. Mostraremos cómo se puede aplicar el mismo procedimiento para modelar cualquier circuito que contenga baterías y resistencias. El procedimiento es el siguiente:

Hacer un buen diagrama del circuito.
Simplifique cualquier resistencia que pueda combinarse fácilmente en resistencias efectivas (en serie o en paralelo).
Haga un nuevo diagrama con las resistencias efectivas, mostrando las flechas de la batería y etiquetando todos los nodos para que los bucles puedan describirse fácilmente.
Hacer una conjetura para las direcciones de la corriente en cada segmento.
Escribe las ecuaciones de regla de cruce.
Escribe las ecuaciones de bucle.
Esto conducirá a ecuaciones$N$ independientes que se pueden resolver para las$N$ diferentes corrientes en el circuito.
Una vez que hayas determinado todas las corrientes, si algunas de ellas son números negativos, cambia la dirección de esas corrientes en el diagrama (serán negativas si adivinaste la dirección incorrectamente).

Ilustraremos el procedimiento en el circuito mostrado en la Figura$\PageIndex{1}$, para lo cual nos gustaría conocer la corriente a través de cada resistor y cada batería. El circuito contiene 5 resistencias ($R_1$-$R_5$), 2 baterías reales (con voltajes ideales$\Delta V_1$ y$\Delta V_2$), y 2 resistencias adicionales para modelar las resistencias internas de las baterías reales ($r_1$,$r_2$)

Figura$\PageIndex{1}$: Un circuito que se puede simplificar y luego resolver con las reglas de Kirchoff.

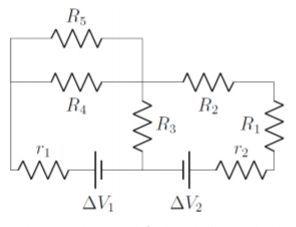
Ejercicio$\PageIndex{1}$

¿Cuántas corrientes diferentes hay en el circuito que se muestra en la Figura$\PageIndex{1}$?

Contestar

Simplificando las resistencias (paso 2): En este circuito, las resistencias$r_2$,$R_1$ y$R_2$ están en serie, para que puedan combinarse en una resistencia efectiva,$R_6$:\[\begin{aligned} R_6=r_2+R_1+R_2\end{aligned}\] Con esta simplificación, obtenemos el circuito ilustrado en la Figura$\PageIndex{2}$

Figura se$\PageIndex{1}$ han combinado en la resistencia efectiva,$R_{6}$, para simplificar el circuito.

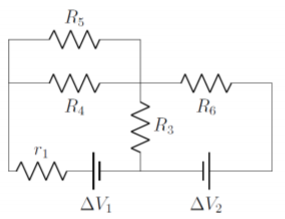
A continuación, observamos que las resistencias$R_4$ y$R_5$ están en paralelo y se pueden combinar fácilmente en una resistencia,$R_7$: la\[\begin{aligned} R_7=\frac{R_4R_5}{R_4+R_5}\end{aligned}\] cual conduce al circuito ilustrado en la Figura$\PageIndex{3}$.

Figura se$\PageIndex{2}$ han combinado en la resistencia efectiva,$R_{7}$, para simplificar el circuito.

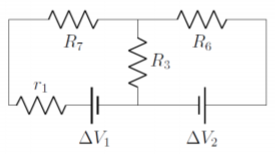
Por último, observamos que$r_1$ y$R_7$ están en serie y se pueden combinar en una resistencia efectiva,$R_8$:\[\begin{aligned} R_8=r_1+R_7=r_1+\frac{R_4R_5}{R_4+R_5}\end{aligned}\] dando lugar al circuito simplificado ilustrado en la Figura$\PageIndex{2}$, que hemos etiquetado con nodos y etiquetas de batería.

Figura$\PageIndex{3}$: se han combinado en la resistencia efectiva,$R_{8}$, para simplificar el circuito.

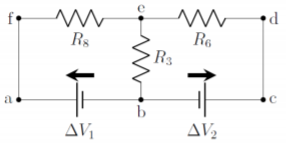
Adivinar las direcciones de las corrientes (paso 4): Antes de que podamos escribir las ecuaciones a partir de las reglas de Kirchhoff, necesitamos etiquetar las corrientes en el diagrama del circuito. En general, no siempre es obvio en qué dirección irán las corrientes, así que hacemos una suposición que podemos arreglar después si adivinamos mal.

Para adivinar las direcciones actuales, elija un punto en el circuito y muévase a lo largo de un segmento. Etiquete la corriente en ese segmento y continúe moviéndose a través del circuito, dividiendo la corriente cuando se encuentre una unión. Asegúrate de tener solo una corriente por segmento. Adivinamos las corrientes de la siguiente manera, haciendo referencia a la Figura$\PageIndex{5}$:

Empezamos en punto$a$ y nos movemos hacia arriba a punto$f$. Vamos a llamar a la corriente en ese segmento,$I_1$.
Como no hay unión, la corriente$I_1$ continúa a través de la resistencia$R_8$ hasta apuntar$e$.
Hay un cruce en el punto$e$, por lo que dividimos la corriente$I_1$ en corrientes$I_2$ (hacia el punto$d$), y$I_3$ (de abajo a punto$b$).
Seguimos$I_2$ primero la corriente;$I_2$ fluye de$e$ a$d$, luego hacia abajo a$c$, a través de la batería$\Delta V_2$, y al punto$b$, donde nuevamente hay cruce.
Seguimos la corriente$I_3$, que simplemente fluye hacia abajo hasta el cruce en el punto$b$, donde “se encuentra” con la corriente$I_2$.
Corrientes$I_2$ y$I_3$ ambas fluyen hacia la unión en el punto$b$, y la corriente que fluye fuera de la unión, a través de la batería$\Delta V_1$, y hacia el punto$a$ es, nuevamente$I_1$, ya que esta corriente luego fluye hasta el punto$f$.
Todos los segmentos de cable tienen una corriente etiquetada, así que terminamos de adivinar las corrientes.

Se puede proceder de manera análoga para cualquier circuito. El circuito final, con corrientes etiquetadas, se muestra en la Figura$\PageIndex{5}$:

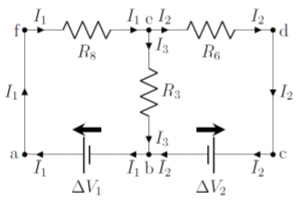
Ahora podemos proceder con el uso de las reglas de Kirchhoff para resolver los valores de las corrientes en el circuito. Es útil señalar que hay 3 corrientes desconocidas en este circuito; así esperamos que las reglas de Kirchhoff nos den 3 ecuaciones independientes.

Aplicando la regla de cruce (paso 5): En el circuito de la Figura$\PageIndex{5}$, hay dos cruces (en puntos$b$ y$e$), por lo que obtendremos dos ecuaciones de la regla de cruce. Para aplicar la regla de cruce, la suma de las corrientes que entran en el cruce debe ser igual a las corrientes que salen de la unión:\[\begin{aligned} \text{incoming currents}&=\text{outgoing currents}&\\ I_2+I_3 &= I_1 \quad &\text{(junction $b$)}\\ I_1 &= I_2+I_3 \quad &\text{(junction $e$)}\\\end{aligned}\] Obsérvese que las dos ecuaciones no son independientes (de hecho, son las mismas). Generalmente se da el caso de que si hay$N$ cruces, se obtendrán ecuaciones menos que$N$ independientes (generalmente,$N-1$ las ecuaciones serán independientes). En este caso, los dos cruces sólo nos dieron una ecuación.

Aplicando la regla de bucle (paso 6): Este circuito contiene 3 bucles diferentes:$abcdefa$,$abefa$, y$bcdeb$, que conducirán a 3 ecuaciones de la regla de bucle. Esperamos que estas ecuaciones no sean independientes, ya que esto conduciría a 4 ecuaciones y 3 incógnitas cuando se combinen con la ecuación de la regla de unión. Empecemos con el bucle$abcdefa$:

De$a$ a$b$, trazamos a través de la batería en sentido contrario a la flecha de la batería:$-\Delta V_1$.
De$b$ a$c$, trazamos a través de la batería en la misma dirección que la flecha de la batería:$+\Delta V_2$.
De$c$ a través$d$ y a través$e$ pasamos por la resistencia$R_6$ en dirección opuesta a la corriente,$I_2$, en esa resistencia:$+I_2R_6$.
De$e$ a$f$, pasamos por el pasar por la resistencia$R_8$ en sentido contrario a la corriente,$I_1$, en esa resistencia:$+I_1R_8$.
Y estamos de vuelta en el punto de partida, por lo que la suma de los términos anteriores es igual a cero.

que da la ecuación:\[\begin{aligned} -\Delta V_1+\Delta V_2+I_2R_6+I_1R_8=0\quad\text{(loop abcdefa)}\end{aligned}\] Del mismo modo$abefa$, para el bucle, obtenemos:\[\begin{aligned} -\Delta V_1+I_3R_3+I_1R_8=0\quad\text{(loop abefa)}\end{aligned}\] y para bucle$bcdeb$:\[\begin{aligned} \Delta V_2+I_2R_6-I_3R_3=0\quad\text{(loop bcdeb)}\end{aligned}\] Aunque parece que hemos obtenido 3 ecuaciones adicionales, sólo dos de estas son independientes. Por ejemplo, si suma la segunda y tercera ecuaciones (bucles$abefa$, y$bcdeb$), simplemente obtiene la primera ecuación (bucle$abcdefa$). En general, si hay$N$ diferentes bucles, se obtendrán ecuaciones menos que$N$ independientes (generalmente ecuaciones$N-1$ independientes, como hicimos aquí).

En este punto, después de elegir una de las ecuaciones de unión, y dos de las ecuaciones de bucle, tenemos 3 ecuaciones independientes que podemos resolver para las 3 corrientes desconocidas ¹:\[\begin{aligned} I_1 &= I_2+I_3 \quad &\text{(junction $e$)}\\ -\Delta V_1+\Delta V_2+I_2R_6+I_1R_8&=0\quad&\text{(loop abcdefa)}\\ -\Delta V_1+I_3R_3+I_1R_8&=0\quad&\text{(loop abefa)}\end{aligned}\] Es solo cuestión de algunas matemáticas simples para resolver para las 3 incógnitas de estas 3 ecuaciones (que nosotros llevar a cabo en el siguiente ejemplo).

Ejemplo$\PageIndex{1}$

Haciendo referencia al circuito de la Figura$\PageIndex{6}$, what is the voltage across the real terminal of the battery with ideal voltage $\Delta V_1$ (the voltage between points $a$ and $b$)? What is the current through resistor $R_5$?

Solución:

Figura$\PageIndex{5}$, con valores rellenados.

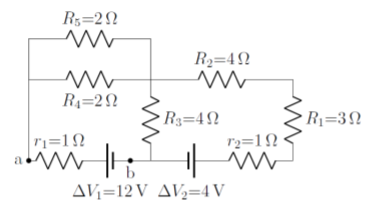
Dado que este circuito es el mismo que acabamos de analizar, sabemos que se puede simplificar en el circuito que se muestra en la Figura$\PageIndex{7}$, con resistencias:\[\begin{aligned} R_6&=r_2+R_1+R_2=(1\Omega)+(3\Omega)+(4\Omega)=8\Omega\\ R_8&=r_1+\frac{R_4R_5}{R_4+R_5}=(1\Omega)+\frac{(2\Omega)(2\Omega)}{(2\Omega)+(2\Omega)}=2\Omega\end{aligned}\]

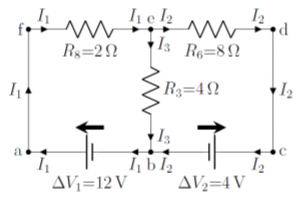
Desde arriba, sabemos que esto lleva a las siguientes tres ecuaciones:

\[\begin{aligned} I_1 &= I_2+I_3 \quad &\text{(junction $e$)}\\ -\Delta V_1+\Delta V_2+I_2R_6+I_1R_8&=0\quad&\text{(loop abcdefa)}\\ -\Delta V_1+I_3R_3+I_1R_8&=0\quad&\text{(loop abefa)}\end{aligned}\]

Para resolver este tipo de ecuaciones, suele ser conveniente colocar los voltajes de la batería en el lado derecho, y los voltajes de la resistencia en el lado izquierdo. Aunque generalmente es una mala práctica rellenar números en las ecuaciones antes de resolverlas, casi siempre es una buena idea a la hora de resolver las$N$ ecuaciones para las$N$ corrientes. Además, para que las ecuaciones sean legibles, también es útil no escribir en las unidades (¡lo cual es muy mala práctica en general!). Así, rellenando los valores para las resistencias y los voltajes de la batería, moviendo los voltajes hacia el lado derecho, obtenemos el siguiente sistema de ecuaciones:

\[\begin{aligned} I_1-I_2-I_3&=0 \quad &\text{(junction $e$)}\\ 2I_1+8I_2&=8 \quad&\text{(loop abcdefa)}\\ 2I_1+4I_3&=12 \quad&\text{(loop abefa)}\end{aligned}\]

Restar la segunda ecuación de la tercera ecuación (para eliminar$I_1$):\[\begin{aligned} 4I_3-8I_2&=4\\ \therefore I_3&=1+2I_2\end{aligned}\] Sustituyendo esto en la ecuación de unión:

\[\begin{aligned} I_1-I_2-I_3&=0\\ I_1-I_2-1-2I_2&=0\\ \therefore I_2=\frac{1}{3}(I_1-1)\end{aligned}\]

Finalmente, sustituyendo esto en la ecuación from loop$abcdefa$, nos permite determinar$I_1$ y las otras dos corrientes:

\[\begin{aligned} 2I_1+8I_2&=8\\ 2I_1+8\left(\frac{1}{3}(I_1-1) \right)&=8\\ \therefore I_1&=\frac{16}{7}=2.29\text{A}\\ \therefore I_2&=\frac{1}{3}(I_1-1)=0.43\text{A}\\ \therefore I_3&=1+2I_2=1.86\text{A}\\\end{aligned}\]

En este caso, las corrientes son todas positivas, por lo que el diagrama de la Figura$\PageIndex{7}$ es correcto y no necesitamos invertir la dirección de ninguna de las corrientes.

Ahora podemos determinar la diferencia de potencial entre los terminales reales de la batería$\Delta V_1$. La corriente a través de la batería es$I_1=2.29\text{A}$, lo que provoca una caída de voltaje,$\Delta V_{r1}$, a través de su resistencia interna,$r_1$ de:

\[\begin{aligned} \Delta V_{r1}=I_1r_1=(2.29\text{A})(1\Omega)=2.29\text{V}\end{aligned}\]

El voltaje a través de los terminales reales de la batería es entonces:\[\begin{aligned} \Delta V_{real}=\Delta V_1-\Delta V_{r1}=(12\text{V})-(2.29\text{V})=9.7\text{V}\end{aligned}\]

La corriente a través de la resistencia$R_5$ (Figura$\PageIndex{6}$) requiere un poco más de reflexión, ya que calculamos la corriente,$I_1$ a través de la resistencia efectiva$R_8$, que ahora debemos “romper”. La figura$\PageIndex{8}$ muestra los componentes de$R_8$.

Figura$\PageIndex{7}$. La corriente,$I_{1}$, que viene de la batería pasa a través$r_{1}$ y luego se divide.

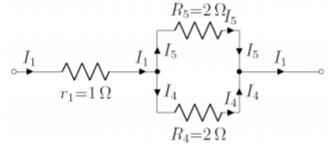
La corriente$I_1$, que pasa por la$\Delta V_1$ batería también pasa por la resistencia$r_1$ interna de la batería. Esa corriente entonces se divide en corrientes,$I_4$ y$I_5$, para pasar por las resistencias$R_4$ y$R_5$. Aunque debería ser obvio que la mitad de$I_1$ pasará por cada resistor (ya que estos son iguales), podemos determinarlo aplicando las reglas de Kirchhoff a la combinación de resistencias en la Figura$\PageIndex{8}$:

\[\begin{aligned} I_1&=I_4+I_5 \quad&\text{(junction)}\\ I_5R_5-I_4R_4&=0\quad&\text{(clockwise loop)}\end{aligned}\]

A partir de la ecuación de bucle, tenemos:

\[\begin{aligned} I_5=\frac{R_4}{R_5}I_4=I_4\end{aligned}\]

ya que$R_4=R_5=2\Omega$. Dado que$I_4=I_5$, la ecuación de unión da:

\[\begin{aligned} I_5=\frac{1}{2}I_1=1.15\text{A}\end{aligned}\]

Al resolver por$I_4$ y$I_5$, ahora hemos determinado todas las corrientes a través de todos los segmentos del circuito original en la Figura$\PageIndex{6}$.

Discusión:

En este ejemplo, mostramos cómo se puede usar un circuito simplificado para resolver la corriente a través de las resistencias efectivas en el circuito simplificado. Una vez que se conocen esas corrientes, demostramos que es sencillo determinar las corrientes a través de resistencias individuales que se han combinado en resistencias efectivas.

Pensamientos de josh

Resolver un circuito puede ser desalentador, especialmente si el diagrama se dibuja de una manera desconocida. Si bien los circuitos de este capítulo están diseñados para ser lo más fáciles de leer posible, muchos circuitos son mucho más extraños. Por ejemplo, aquí hay un circuito con el que puede encontrarse:

Figura$\PageIndex{9}$: Un circuito de aspecto extraño.

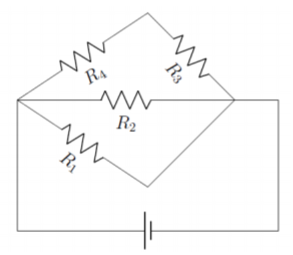
El circuito en la Figura$\PageIndex{9}$ Puede parecer que es un circuito difícil de resolver, pero el diagrama se puede volver a dibujar para revelar la simplicidad del circuito:

Figura$\PageIndex{10}$: Un circuito de aspecto mucho menos extraño.

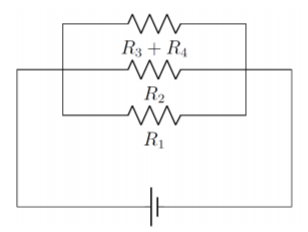
Lo que solía ser una extraña forma de cometa ahora es solo un circuito paralelo, que se puede simplificar aún más calculando la resistencia efectiva:\[\begin{aligned} R_{eff} &= (R_1^{-1}+R_2^{-1}+(R_3+R_4)^{-1})^{-1}\end{aligned}\] Lo que da un circuito en serie con solo una resistencia:

Figura$\PageIndex{11}$: Un circuito sencillo.

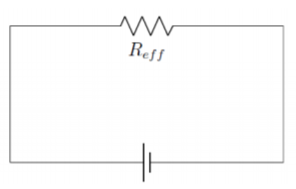
Los circuitos se pueden dibujar de muchas maneras únicas o potencialmente confusas, pero saber leer el circuito y volver a dibujarlo puede ayudar a que el diagrama sea más legible y el circuito sea más fácil de resolver.

Notas al pie

1. Las 3 incógnitas no necesariamente tienen que ser las corrientes, y podrían ser cualquier combinación de las corrientes, voltaje de la batería y resistencias. Siempre y cuando haya como máximo 3 cantidades desconocidas, se podrá resolver este circuito.