20.5: Modelado de circuitos con capacitores

revisar temas

• Sección 18.5 sobre capacitores.

Hasta el momento, hemos modelado circuitos donde la corriente no cambia con el tiempo. Cuando se incluye un condensador en un circuito, la corriente cambiará con el tiempo, ya que el condensador se carga o se descarga. El circuito mostrado en la Figura\(\PageIndex{1}\) muestra una batería ideal ¹ (\(\Delta V\)), en serie con una resistencia (\(R\)), un condensador (\(C\), dos barras verticales) y un interruptor (\(S\)) que está abierto.

Figura\(\PageIndex{1}\): Un circuito simple con una resistencia, batería y condensador.

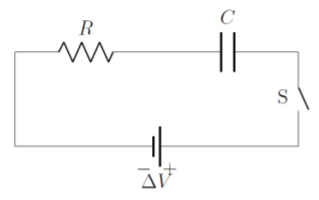
Cuando el interruptor está abierto, la corriente no puede fluir a través del circuito. Si asumimos que el condensador no tiene carga en él, una vez que cerramos el interruptor, la corriente comenzará a fluir y las cargas se acumularán en el condensador. Los electrones saldrán del terminal negativo de la batería, fluirán a través de la resistencia y se acumularán en el lado izquierdo del condensador, el cual adquiere una carga negativa. Esto empuja los electrones fuera del lado derecho del condensador, que luego se carga positivamente. Los electrones del lado positivo del condensador luego fluyen hacia el lado positivo de la batería, completando el circuito.

Eventualmente, las cargas en el condensador se acumularán hasta cierto punto en el que impidan cualquier flujo adicional de corriente. Una vez que el lado izquierdo del condensador está al mismo potencial que el lado izquierdo de la batería, la corriente dejará de fluir. Es decir, eventualmente, la diferencia de potencial a través del condensador será igual a la de la batería, y podemos pensar en esto como un circuito utilizado para cargar un condensador. La corriente es alta cuando el interruptor se abre por primera vez, pero finalmente baja a cero a medida que se carga el condensador. Por lo tanto, la corriente depende del tiempo.

Podemos modelar este circuito simple (con el interruptor cerrado) usando la regla de bucle de Kirchhoff. La suma de los voltajes a través de cada componente debe sumarse a cero:\[\begin{aligned} \Delta V - IR - \frac{Q}{C} = 0\end{aligned}\] donde usamos el hecho de que la carga,\(Q\), en un condensador está relacionada con la diferencia de potencial,\(\Delta V_C\), a través del condensador por\(Q=C\Delta V_C\). La corriente,\(I\), es la velocidad a la que las cargas fluyen a través del circuito, y por lo tanto es igual a la velocidad a la que se acumulan las cargas en el condensador:\[\begin{aligned} I=\frac{dQ}{dt}\end{aligned}\] Sustituyendo esto en la ecuación de bucle, obtenemos una ecuación diferencial separable para la carga en el condensador en función de tiempo,\(Q(t)\):\[\begin{aligned} \Delta V - IR - \frac{Q}{C} &= 0\\ \Delta V - \frac{dQ}{dt}R - \frac{Q}{C} &= 0\\ \Delta V - \frac{Q}{C} &= \frac{dQ}{dt}R\\ C\Delta V - Q &= RC\frac{dQ}{dt}\\ \therefore \frac{dt}{RC}&=\frac{dQ}{C\Delta V - Q }\end{aligned}\] Esto es similar a las ecuaciones diferenciales que hemos resuelto previamente (de hecho, es la misma ecuación que en el Ejemplo 6.2.3 donde observamos el efecto del arrastre dependiente de la velocidad). La solución a la ecuación, asumiendo que el interruptor está cerrado en\(t=0\), viene dada por un exponencial:\[\begin{aligned} Q(t) = C\Delta V\left( 1 - e^{-\frac{t}{RC}} \right)\end{aligned}\] Así, la carga en el condensador comienza en cero cuando el interruptor está cerrado, y crece asintóticamente hasta que alcanza un valor de\(Q=C\Delta V\), que corresponde a el condensador tiene la misma diferencia de potencial a través de él que la batería. El valor\(\tau=RC\) se llama la “constante de tiempo” del circuito RC, y corresponde al tiempo en el que el condensador alcanzará aproximadamente\((1-e^{-1})=63\%\) su carga máxima. La corriente en función del tiempo viene dada por:\[\begin{aligned} I(t)=\frac{dQ}{dt}=\frac{\Delta V}{R}e^{-\frac{t}{RC}}\end{aligned}\] y podemos ver que en\(t=0\) el momento la corriente es la misma que si no hubiera condensador presente, y la corriente entonces disminuye exponencialmente hasta llegar a cero.

Notas al pie

1. El modelo aún se mantiene para una batería real, ya que la resistencia interna de la batería solo se puede incluir en la resistencia de la resistencia,\(R\).