21.2: La fuerza magnética sobre una carga móvil

revisar temas

Sección A1.3 sobre el producto vector.

Cuando una carga eléctrica,\(q\), tiene una velocidad,\(\vec v\), relativa a un campo magnético,\(\vec B\), se ejerce una fuerza magnética sobre la partícula:

\[\vec F_{B}=q\vec v\times\vec B\]

Podemos hacer algunas observaciones sobre la fuerza magnética:

• La fuerza magnética siempre es perpendicular a la velocidad y al campo magnético (ya que viene dada por su producto cruzado).
• La dirección de la fuerza magnética depende del signo de la carga.
• La fuerza magnética no puede hacer trabajo, ya que siempre es perpendicular a la velocidad (y por lo tanto al desplazamiento).
• No hay fuerza si la velocidad de la partícula está en la misma dirección que el vector de campo magnético.
• La fuerza aumenta con la carga, la velocidad y la fuerza del campo magnético.

Ejercicio\(\PageIndex{1}\)

Un protón se mueve hacia el Este en el campo magnético de la Tierra, ¿en qué dirección se desvía?

1. Lejos de la Tierra.
2. Hacia la Tierra.
3. Norte.
4. Sur.

Contestar

Ejercicio\(\PageIndex{2}\)

Un electrón se mueve hacia el Oeste en el campo magnético de la Tierra, ¿en qué dirección se desvía?

1. Lejos de la Tierra.
2. Hacia la Tierra.
3. Norte.
4. Sur.

Contestar

Pensamientos de josh

Es muy importante recordar lo que representa cada parte de la regla de la mano derecha para productos cruzados. Para ayudar a recordar lo que representa cada dedo, digo “velocidad” a medida que extiendo mi pulgar, “campo” a medida que extiendo mi dedo índice, y “fuerza” a medida que extiendo mi dedo medio. Al usar la regla de la mano derecha, también es importante recordar la\(q\) en la ecuación\(\vec F_B = q\vec v \times \vec B\). Esto\(q\) podría ser negativo, lo que significaría que la fuerza actúa en sentido contrario.

Figura\(\PageIndex{1}\): La forma en que Josh recuerda la regla de la mano derecha para el magnetismo.

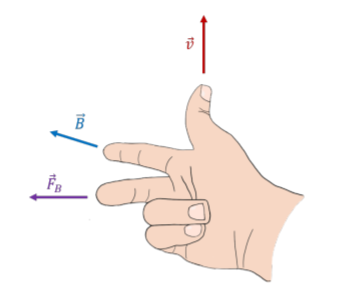
Si te encuentras olvidando la regla de la derecha en una prueba o examen, solo recuerda que aún puedes encontrar la respuesta correcta configurando un sistema de coordenadas tridimensional y evaluando el producto cruzado.

Debería estar algo molesto por el hecho de que la fuerza depende de la velocidad de la carga, ya que la velocidad depende del marco de referencia desde el que se mide. La ecuación anterior tiene una extraña implicación: si observamos un electrón moviéndose en un campo magnético, veremos que su movimiento es desviado por el campo magnético. Si nos movemos junto con el electrón, para que tenga una velocidad de cero en nuestro marco de referencia, no deberíamos ver al electrón siendo desviado, ya que la fuerza magnética sería cero. Claramente, el movimiento del electrón no puede depender del marco de referencia desde el que lo observemos. Así, la única forma en que esta ecuación puede tener sentido es si el campo magnético también depende de nuestro marco de referencia. Revisaremos esto en un capítulo posterior, pero por ahora, recordemos que esta ecuación sólo tiene sentido si la velocidad se mide en el mismo marco de referencia que aquel en el que se define el campo magnético.

Otro tema molesto con la fuerza magnética es que parece depender del hecho de que la mayoría de los humanos son diestros. En efecto, la dirección de la fuerza requiere que se utilice la regla de la derecha, que parece arbitraria. Esta es una ocurrencia común en la física, ya que muchas cantidades se definen usando un producto cruzado. Sin embargo, ninguna cantidad física puede depender de nuestra elección de mano derecha o izquierda para determinar productos cruzados. Resulta que cualquier cantidad física (como la fuerza sobre una partícula, que desviará la partícula en una dirección claramente identificable que no depende de la elección del ser humano de derecha e izquierda), siempre depende de dos aplicaciones sucesivas de la regla de la derecha. En este caso, la dirección del campo magnético también viene dada por una regla de la derecha aplicada a las cargas móviles que crean el campo (como veremos en el siguiente capítulo). Los sucesivos usos de la mano derecha “cancelan” dos veces; uno encuentra que una carga se desvía en la misma dirección si se hubiera usado la mano izquierda para definir el campo magnético, ¡y luego otra vez la izquierda para el producto cruzado! Volveremos a visitar este número en el próximo capítulo.

Considera el movimiento de una partícula cargada en una región donde el campo magnético es uniforme (constante en magnitud y dirección). Si el vector de velocidad de la partícula es perpendicular al campo magnético, la partícula experimentará un movimiento circular uniforme, como se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): El movimiento de una partícula cargada en un campo magnético uniforme (fuera de la página) es un movimiento circular uniforme.

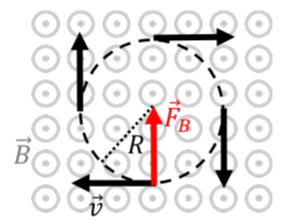
En efecto, la fuerza es siempre perpendicular a la velocidad, y la fuerza es constante en magnitud ya que tanto la velocidad como el campo magnético permanecen constantes. Estas son las únicas condiciones requeridas para un movimiento circular uniforme. Podemos determinar fácilmente el radio,\(R\), del círculo, ya que la fuerza magnética es responsable de la aceleración centrípeta:\[\begin{aligned} F_B &= m\frac{v^2}{R}\\ qvB &= m\frac{v^2}{R}\\ \therefore R &= \frac{mv}{qB}\end{aligned}\] El radio se llama el “radio ciclotrón”.

Ejercicio\(\PageIndex{3}\)

¿La partícula ilustrada en la Figura está cargada\(\PageIndex{2}\) positiva o negativamente?

1. La partícula está cargada positivamente.
2. La partícula está cargada negativamente.
3. No hay suficiente información para contar.
4. La partícula no tiene cargo.

Contestar

Haciendo referencia a la Figura\(\PageIndex{2}\), si la velocidad de la partícula está en el plano de la página (perpendicular al campo magnético), como se ilustra, la partícula sufrirá un movimiento circular uniforme. Si la velocidad de la partícula tiene un componente que es paralelo al campo magnético (por ejemplo, un componente que sale de la página, hacia usted), la partícula sufrirá “movimiento helicoidal” (una espiral). El radio de la hélice está determinado por el componente de la velocidad,\(\vec v_{\perp}\), es decir perpendicular al campo magnético:\[\begin{aligned} \therefore R &= \frac{mv_{\perp}}{qB}\end{aligned}\]

La partícula cargada también tendría un componente de velocidad hacia ti que es constante, resultando en el movimiento espiral ilustrado en la Figura\(\PageIndex{3}\). Obsérvese que la distancia entre dos espirales (etiquetada\(h\) en la figura) se denomina “paso”, y está determinada por el componente de velocidad que es paralelo al campo magnético\(\vec v_\parallel\), ya que ese componente no se ve afectado por la fuerza magnética.

Figura\(\PageIndex{3}\): El movimiento helicoidal de una partícula cargada con un componente de velocidad paralelo al campo magnético. A la distancia,\(h\), entre espirales se le llama el “tono”.

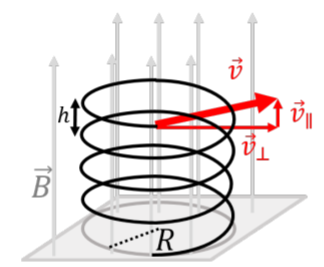
Ejemplo\(\PageIndex{1}\)

Se observa que una partícula de carga desconocida y masa desconocida experimenta un movimiento circular uniforme con un periodo,\(T\), when traveling perpendicular to a uniform magnetic field, \(B\). What is the ratio of the particle’s charge to its mass, \(q/m\)?

Solución:

Podemos usar el período del movimiento para determinar la velocidad de la partícula en términos del radio de la trayectoria circular:\[\begin{aligned} v = \frac{2\pi R}{T}\end{aligned}\] y luego usar la ecuación para el radio del ciclotrón para relacionarlo con la relación carga-masa de la partícula:\[\begin{aligned} R &= \frac{mv}{qB}\\ &= \frac{2\pi R m}{qBT}\\ \therefore \frac{q}{m} &= \frac{2\pi}{BT} \end{aligned}\]

Discusión:

Cuando una partícula cargada experimenta un movimiento circular uniforme en un campo magnético, el radio del movimiento depende de la relación carga-masa de la partícula. Esto a menudo se puede utilizar para medir la masa de, digamos, un ion, si se conoce la carga del ion (generalmente una o dos unidades de la carga electrónica). Un espectrómetro de masas hace uso de este principio para determinar la composición de una muestra. La muestra se vaporiza e ioniza, los iones se aceleran luego usando una diferencia de potencial eléctrico, antes de que experimenten un movimiento circular uniforme. Los iones de diferentes masas (y la misma carga) sufrirán entonces un movimiento circular con diferentes radios, lo que permite determinar sus masas, y así conocer la composición de la muestra.