21.4: El par de torsión en un bucle de transporte de corriente

Última actualización
Guardar como PDF

Page ID: 128976

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Revisar temas

Sección 11.3 sobre par.
Sección 16.4 sobre dipolos eléctricos.

Como se señala en el Ejemplo 21.3.1, la fuerza magnética neta sobre cualquier bucle cerrado sumergido en un campo magnético uniforme es cero. Consideremos, por ejemplo, el bucle rectangular portador de corriente de altura,\(h\), y ancho,\(w\), sumergido en un campo magnético uniforme,\(\vec B\), como se ilustra en la Figura\(\PageIndex{1}\) (nótese que el campo no es perpendicular al plano del bucle, como lo fue en Ejemplo 21.3.1).

Figura\(\PageIndex{1}\): Bucle rectangular que transporta corriente en sentido contrario a las agujas del reloj en un campo magnético uniforme.

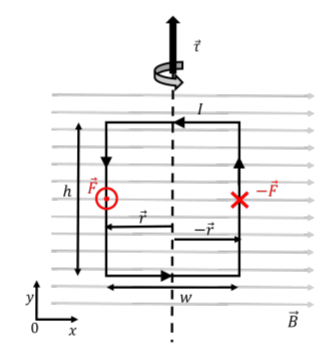
La fuerza magnética en las dos secciones horizontales del cable es cero, ya que la corriente es colineal con el campo magnético a lo largo de esas secciones. En la sección vertical izquierda (con corriente que fluye hacia abajo), la fuerza magnética está fuera de la página (\(z\)dirección positiva), y viene dada por:\[\begin{aligned} \vec F = IhB\hat z\end{aligned}\] Del mismo modo, la fuerza en la sección vertical derecha (con corriente que fluye hacia arriba) tendrá la misma magnitud pero la dirección opuesta. La fuerza neta en el bucle es, por lo tanto, cero.

Sin embargo, el par neto en el bucle alrededor de su eje vertical de simetría (mostrado por la línea discontinua vertical en la figura) no es cero. El par total se encuentra sumando los pares de torsión de las fuerzas ejercidas sobre las dos secciones verticales de alambre:\[\begin{aligned} \vec \tau &= \vec r\times \vec F + (-\vec r \times - \vec F)\\ &= 2 \vec r \times F = 2 \left(-\frac{w}{2}\hat x\right) \times IhB\hat z = IBwh (-\hat x\times \hat z)\\ \therefore \vec \tau&=IBwh (\hat y)\end{aligned}\] donde\(\vec r\) está el vector desde el eje de rotación hasta la ubicación donde se ejerce la fuerza.

Momento dipolo magnético

Describir el par en un bucle puede ser difícil en tres dimensiones, por lo que introducimos el “momento dipolo magnético” para simplificar la descripción.

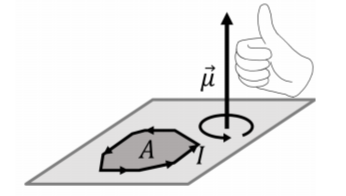
Si un bucle cerrado lleva una corriente,\(I\), el vector de momento dipolo magnético,\(\vec \mu\), se define de tal manera que tiene una magnitud:\[\begin{aligned} \mu = IA\end{aligned}\] donde,\(A\), es el área encerrada por el bucle. La dirección del vector de momento dipolo magnético es tal que es perpendicular a la superficie definida por el bucle. De las dos direcciones posibles de este tipo, la dirección del momento dipolar magnético viene dada por la regla de la derecha para vectores axiales; al enrollar los dedos en la dirección de la corriente, el pulgar apuntará en la dirección del momento dipolar magnético. Esto se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): La regla de la derecha para vectores axiales se utiliza para determinar la dirección del vector de momento dipolo magnético para un bucle que transporta corriente,\(I\).

En cuanto al momento dipolar magnético, el par en un bucle, con momento dipolo magnético\(\vec \mu\), sumergido en un campo magnético\(\vec B\), viene dado por:

\[\vec\tau = \vec\mu\times\vec B\]

La magnitud del par viene dada por:\[\begin{aligned} \tau =\mu B \sin\theta\end{aligned}\] donde\(\theta\) está el ángulo entre el momento dipolo magnético y los vectores de campo magnético.

Podemos verificar que esta fórmula da el par correcto para el bucle rectangular en la Figura\(\PageIndex{1}\) que calculamos anteriormente. El momento dipolar magnético de ese bucle viene dado por:\[\begin{aligned} \vec \mu = IA \hat z = Iwh\hat z\end{aligned}\] donde la dirección del vector viene dada por la regla de la derecha para vectores axiales (fuera de la página, ya que la corriente está en sentido contrario a las agujas del reloj en la Figura\(\PageIndex{1}\)). El par en el bucle es así:\[\begin{aligned} \vec \tau = \vec \mu \times \vec B = (Iwh\hat z) \times (B\hat x) = IBwh (\hat y)\end{aligned}\] como encontramos anteriormente.

El momento dipolo magnético se puede utilizar para describir un bucle portador de corriente en un campo magnético. Es decir, en lugar de dibujar un bucle que transporta corriente, podemos dibujar de manera equivalente simplemente el vector de momento dipolo magnético asociado. Esto es útil porque el vector de momento dipolo magnético se comporta de la misma manera que un imán de barra (con la punta de la flecha actuando como un polo Norte). En efecto, un campo magnético siempre creará un par que intentará alinear el momento dipolo magnético con el campo magnético, así como la aguja de una brújula experimenta un par si no está alineada con el campo magnético de la Tierra. El par del campo magnético es entonces cero cuando el momento dipolo magnético es paralelo al campo magnético (ya que el producto cruzado entre vectores colineales es cero).

La figura\(\PageIndex{3}\) muestra una manera de visualizar un bucle portador de corriente en un campo magnético utilizando su vector de momento dipolo magnético,\(\vec mu\).

Figura\(\PageIndex{3}\): Tres bucles de corriente con diferentes orientaciones relativas a un campo magnético uniforme. Los bucles se ven desde arriba, y la corriente se muestra entrando y saliendo de la página en cada bucle, junto con el vector de momento dipolo magnético correspondiente.

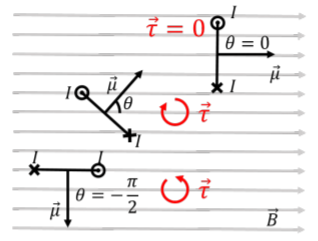
Se muestran tres bucles (como líneas), vistos desde arriba, y la dirección de la corriente en cada bucle se muestra como entrando o saliendo de la página. Equivalentemente, uno puede simplemente dibujar el vector de momento dipolo magnético para cada bucle (perpendicular al plano del bucle). Para el bucle superior, el momento dipolo magnético es paralelo al campo magnético, por lo que el campo magnético no ejerce par. Para el bucle medio, el momento dipolo magnético forma un ángulo\(\theta\) con el vector de campo magnético, de modo que el par en ese bucle tiene una magnitud dada por\(\tau=\mu B \sin\theta\), y apunta hacia la página (rotación en sentido horario). El bucle inferior forma un ángulo\(-\pi/2\) con el campo magnético, lo que resulta en un par en sentido contrario a las agujas del reloj. En todos los casos, el par es tal que siempre trata de alinear el vector de momento dipolo magnético con el campo magnético, así como si el momento dipolo magnético fuera la aguja de una brújula.

Ejemplo\(\PageIndex{1}\)

Determina el momento dipolar magnético del electrón que orbita un átomo de hidrógeno, si asumes que el electrón está en una órbita circular con un radio de\(R=0.5\unicode{xC5}\).

Solución:

A medida que el electrón orbita alrededor del círculo, resulta en un bucle circular de corriente,\(I\). La corriente es la velocidad a la que la carga pasa por un punto por unidad de tiempo. Si la órbita electrónica tiene un periodo\(T\), entonces la corriente correspondiente,\(I\), viene dada por:

\[\begin{aligned} I=\frac{\Delta Q}{\Delta t} = \frac{e}{T}\end{aligned}\]

La fuerza centrípeta sobre el electrón es proporcionada por la fuerza Coulomb\(F_C\),, ejercida por el protón, que nos permite obtener la velocidad orbital, y así el periodo de la órbita:

\[\begin{aligned} F_C &= m\frac{v^2}{R}\\ k\frac{e^2}{R^2}&= m\frac{v^2}{R}\\ \therefore v &=\sqrt{\frac{ke^2}{mR}}\\ \therefore T &= \frac{2\pi R}{v}\end{aligned}\]

El momento dipolo magnético viene dado entonces por:

\[\begin{aligned} \mu &=IA = \frac{e}{T}\pi R^{2}=\frac{ev}{2\pi R}\pi R^{2}\frac{1}{2}evR=\frac{1}{2}\sqrt{\frac{ke^{4}R}{m}} \\ &=\frac{1}{2}\sqrt{\frac{(9\times 10^{9}\text{N/C}^{2}\cdot\text{m}^{2})(1.6\times 10^{-19}\text{C})^{4}(0.5\unicode{xC5})}{(9.1\times 10^{-31}\text{kg})}}=9\times 10^{24}\text{A}\cdot\text{m}^{2} \end{aligned}\]

Discusión:

En este ejemplo calculamos el momento dipolar magnético orbital del electrón en un átomo de hidrógeno. Este fue un modelo muy sencillo, ya que en realidad, los electrones no orbitan átomos en órbitas circulares, y se debe utilizar la mecánica cuántica para describir el movimiento con precisión.

Energía potencial para un momento magnético en un campo magnético

Un momento dipolo magnético en un campo magnético se comporta de la misma manera que un dipolo eléctrico en un campo eléctrico. Por analogía, entonces podemos definir una energía potencial\(U\), para un momento dipolar magnético,\(\vec \mu\) en un campo magnético,\(\vec B\):

\[U=-\vec\mu\cdot\vec B=-\mu B\cos\theta\]

donde\(\theta\) está el ángulo entre el momento magnético y el campo magnético. Si un dipolo magnético no está alineado con un campo magnético y se libera, comenzará a girar (ganará energía cinética rotacional) hasta alcanzar un mínimo en energía potencial (\(\theta = 0\)). El momento magnético oscilaría de un lado a otro\(\theta =0\) si no hay pérdidas. Obsérvese que el punto donde\(\theta = \pi\), es un equilibrio inestable.

Ejercicio\(\PageIndex{1}\)

Cuando un momento dipolo magnético es paralelo con un campo magnético y apunta en la misma dirección que el campo magnético, tendrá...

... su par máximo y máxima energía potencial.
... su par máximo y energía potencial mínima.
... su par mínimo y máxima energía potencial.
... su par mínimo y energía potencial mínima.

Contestar

Ejercicio\(\PageIndex{2}\)

Cuando se coloca un momento dipolo magnético de tal manera que se maximiza el par del campo magnético, tendrá...

... cero energía potencial.
... su mínima energía potencial.

Contestar