21.9: Problemas y soluciones de la muestra

Ejercicio\(\PageIndex{1}\)

Un tubo de rayos catódicos en un televisor acelera un electrón usando una diferencia de potencial de\(\Delta V=500\text{V}\). The electron must be deflected upwards by a distance \(h=3\text{cm}\) using a uniform magnetic field, \(\vec B\), before striking the phosphorescent screen, which is a distance \(d= 5\text{cm}\) away. What direction and magnitude must the magnetic field have in order to steer the electron towards its destination?

Contestar

Primero, determinamos la velocidad del electrón que se aceleró sobre una diferencia de potencial de\(\Delta V=500\text{V}\). Su energía cinética viene dada por su carga multiplicada por la diferencia de potencial::\[\begin{aligned} K &= e\Delta V \\ \frac{1}{2} mv^2 &= e\Delta V\\ \therefore v &= \sqrt{\frac{2e\Delta V}{m}}= \sqrt{\frac{2(1.602\times 10^{-19}\text{C})(500\text{V})}{(9.109\times 10^{-31}\text{kg})}}\\ &= 1.326\times 10^{7}\text{ms}^{-1}\end{aligned}\] Ahora que tenemos la velocidad, debemos determinar la dirección del campo magnético. Sabemos que el electrón se mueve directamente hacia la pantalla fosforescente (que definiremos como\(\vec x\)) y el electrón debe desviarse directamente hacia arriba (que definiremos como\(\vec z\)). Sabiendo esto, podemos usar la regla de la mano derecha para determinar rápidamente que la fuerza magnética estará actuando en la\(-\vec y\) dirección.

En la región con campo magnético, el electrón experimentará un movimiento circular uniforme con un radio dado por el radio del ciclotrón,\(R\):\[\begin{aligned} R=\frac{mv}{qB}\end{aligned}\]

Por lo tanto, necesitamos determinar el radio de ese círculo para que el electrón llegue a esa ubicación deseada en la pantalla. Una sección del círculo alrededor del cual se mueve el electrón se ilustra en la Figura\(\PageIndex{1}\).

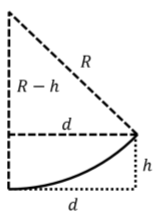
Figura\(\PageIndex{1}\): Deflexión de una novación de electrones en un campo magnético uniforme.

De la geometría y el teorema de Pitágoras, tenemos:\[\begin{aligned} R^2 &= (R-h)^2+d^2\\ R^2 &= R^2-2Rh+h^2+d^2\\ \therefore R &= \frac{h^2+d^2}{2h}=\frac{(3\text{cm})^2+(5\text{cm})^2}{2(3\text{cm})}=5.67\text{cm}\end{aligned}\] La fuerza del campo magnético viene dada entonces por:\[\begin{aligned} B&=\frac{mv}{qR}=\frac{(9.11\times 10^{-31}\text{kg})(1.326\times 10^{7}\text{ms}^{-1})}{(1.6\times 10^{-19}\text{C})(0.0567\text{m})}=0.00135\text{T}\end{aligned}\]

Ejercicio\(\PageIndex{2}\)

Un galvanómetro tiene una bobina cuadrada con una longitud lateral de\(a=2.5\text{cm}\) and \(N=70\) loops between two magnets which generate a radial magnetic field of \(B=8\text{mT}\). When a current runs through the coil, it generates a torque which is opposed by a spring with a torsional spring constant of \(\kappa = 1.5\times 10^{-8}\text{Nmrad}^{-1}\). If the deflection of the galvanometer’s needle is \(0.7\), what is the current running through the coil?

Contestar

Primero, determinaremos el momento dipolar magnético de la bobina cuadrada:\[\begin{aligned} \mu &= NIA\\ \mu &=NIa^2\end{aligned}\] Ahora que tenemos el momento dipolo magnético, podemos calcular el par en la bobina cuadrada que es producido por el campo magnético. Obsérvese que, en un galvanómetro, el campo magnético está configurado de tal manera que sea radial y siempre perpendicular al momento dipolar magnético de la bobina:\[\begin{aligned} \tau_B &= N\mu B sin(90^{\circ})= NIa^2B\\\end{aligned}\] La deflexión\(\theta\),, para una corriente dada ocurrirá cuando el par producido por el cable sea igual al par producido por el primavera. El par producido por el resorte viene dado por:\[\begin{aligned} \tau_s =\kappa \theta\end{aligned}\] donde\(\theta\) se mide en radianes. La ecuación anterior es el equivalente rotacional de la Ley de Hooke. Igualando el par del resorte y del campo magnético, podemos determinar la corriente:\[\begin{aligned} \tau_B&=\tau_S\\ NIa^2B &= \kappa \theta\\ I &= \frac{\kappa \theta}{Na^2B} = \frac{(1.5\times 10^{-8}\text{Nm(rad)}^{-1}) (0.7\text{rad})}{70(0.025\text{m})^2(8\times 10^{-3}\text{T})}\\ &= 30\mu\text{A}\end{aligned}\]

Ejercicio\(\PageIndex{3}\)

Integrar la ecuación\(d\vec F = Id\vec l \times \vec B\) over a circular path to show that the torque exerted on a circular loop of radius, \(R\), carrying current, \(I\), immersed in a uniform magnetic field, \(\vec B\), has a magnitude given by \(\tau=\mu B\), where \(\vec \mu\) is the magnetic dipole moment of the loop. You may simplify the problem by modeling the loop when its magnetic moment is perpendicular to the magnetic field.

Contestar

La figura\(\PageIndex{2}\) ilustra un bucle de radio,\(R\), llevando corriente,\(I\). El bucle está en el\(x-z\) plano, y hay un campo magnético,\(\vec B\), en la\(x\) dirección negativa. Al configurar el bucle de esta manera, es más fácil visualizar algunos de los aspectos tridimensionales.

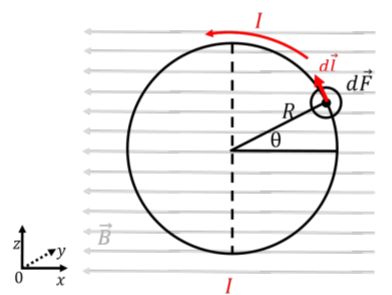
Figura\(\PageIndex{2}\): Un bucle portador de corriente en un campo magnético.

Considera una sección infinitesimal del bucle, con longitud,\(dl\), ubicada en el bucle en una posición etiquetada por el ángulo,\(\theta\), como se ilustra. El vector,\(d\vec l\), viene dado por:\[\begin{aligned} d\vec l = dl (-\sin\theta \hat x + \cos\theta \hat z)\end{aligned}\] La fuerza magnética sobre ese elemento del bucle viene dada por:\[\begin{aligned} d\vec F &=Id\vec l \times \vec B\\ &=Idl(-\sin\theta \hat x + \cos\theta \hat z) \times (-B\hat x)\\ &=-IBdl\cos\theta (\hat z \times \hat x)\\ &=-IBdl\cos\theta\hat y\end{aligned}\] y la fuerza sobre ese elemento de alambre está fuera de la página (\(y\)dirección negativa), como se ilustra. Esa fuerza infinitesimal creará un par infinitesimal:\[\begin{aligned} d\vec \tau = \vec r \times d\vec F\end{aligned}\] donde\(\vec r\) está el vector desde el eje de rotación (a través del centro del bucle, paralelo al\(z\) eje) hasta el punto donde se ejerce la fuerza. La longitud del vector,\(\vec r\), es simplemente\(r=R\cos\theta\), y la fuerza es perpendicular al vector\(\vec r\). Así, el par en el elemento infinitesimal viene dado por:\[\begin{aligned} d\vec \tau &= \vec r \times d\vec F= (R\cos\theta \hat x)\times (-IBdl\cos\theta\hat y)\\ &=-IBR\cos^2\theta dl (\hat x \times \hat y)=-IBR\cos^2\theta dl \hat z\end{aligned}\] y el par en ese elemento infinitesimal está en la\(z\) dirección negativa, como se anticipa desde la dirección de la fuerza. Tenga en cuenta que si hubiéramos considerado que el bucle estuviera orientado de tal manera que el campo magnético no esté en el plano del bucle, el vector\(\vec r\) en el par tendría un componente en la\(y\) dirección.

Podemos sumar los pares de torsión en cada elemento del bucle, de\(\theta = 0\) a\(\theta=2\pi\). Podemos expresar la longitud\(dl\), usando el ángulo infinitesimal,\(d\theta\), que subtiende el arco de longitud,\(dl\), en el círculo de radio,\(R\):\[\begin{aligned} dl = Rd\theta\end{aligned}\]

El par neto viene dado entonces por:\[\begin{aligned} \vec \tau &= \int d\vec \tau=\int -IBR\cos^2\theta dl \hat z= (-IBR^2\hat z)\int_0^{2\pi} \cos^2\theta d\theta =(-IBR^2\hat z)\pi\end{aligned}\] El momento magnético del bucle es: de\[\begin{aligned} \mu = IA = I\pi R^2\end{aligned}\] modo que el par de torsión es dado de hecho por\(\tau = \mu B\). Si hubiéramos girado el bucle para que el vector\(\vec r\),, tuviera un\(y\) componente, entonces habríamos encontrado la fórmula general con un producto cruzado.