22.1: La Ley Biot-Savart

La ley Biot-Savart nos permite determinar el campo magnético en alguna posición del espacio que se debe a una corriente eléctrica. Más precisamente, la ley Biot-Savart permite calcular el campo magnético infinitesimal,\(d\vec B\), que es producido por una pequeña sección de alambre,\(d\vec l\), llevando corriente,\(I\), tal que\(d\vec l\) es colineal con el alambre y apunta en la dirección de la corriente eléctrica:

\[d\vec B=\frac{\mu_{0}I}{4\pi}\frac{d\vec l\times\hat r}{r^{2}}\]

donde,\(\vec r\), es el vector desde el elemento de alambre,\(d\vec l\), hasta el punto donde nos gustaría determinar el campo magnético, como se ilustra en la Figura\(\PageIndex{1}\). \(µ_{0}\)es una constante de proporcionalidad llamada la “permeabilidad del espacio libre”, y tiene el valor\(µ_{0} = 4π × 10^{−7}\text{T} ·\text{m/A}\).

Figura\(\PageIndex{1}\): El campo magnético infinitesimal,\(d\vec B\), que es creado por una sección infinitesimal de alambre,\(d\vec l\), transportando corriente\(I\). Tenga en cuenta que el vector\(\vec r\),, va desde\(d\vec l\) hasta el punto donde deseamos calcular el campo.

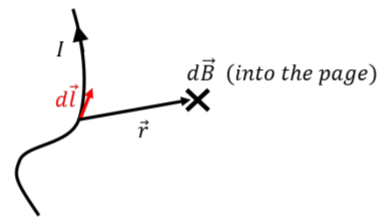
La Ley Biot-Savart tiene algunas similitudes con la Ley Coulomb para calcular el campo eléctrico, ya que la magnitud del campo magnético disminuye a medida que la inversa de la distancia cuadrada entre la fuente y el campo. Sin embargo, solo se puede expresar en forma diferencial (es decir, como infinitesimal), y requiere trabajar en tres dimensiones, debido al producto cruzado. Por lo general, es más conveniente utilizar la Ley Biot-Savart en la forma:

\[\begin{aligned}d\vec B = \frac{\mu_{0}I}{4\pi}\frac{d\vec l\times \vec r}{r^{3}} \end{aligned}\]

donde se\(\hat r\) sustituyó el vector unitario por\(\vec r/r\).

El procedimiento para aplicar la Ley Biot-Savart es el siguiente

HowTo: Aplicación de la Ley Biot-Savart

1. Haz un diagrama realmente bueno, ya que tendrás que incluir algunos aspectos 3D.
2. Elija una sección infinitesimal de alambre,\(d\vec l\).
3. Determinar el vector\(\vec r\).
4. Determinar el producto cruzado\(d\vec l ×\vec r\),, que apuntará en la dirección del campo magnético desde esa sección infinitesimal de alambre.
5. Escriba el vector\(d\vec B\) infinitesimal y determine sus componentes.
6. ¡Piensa en la simetría! Al sumar el\(d\vec B\), ¿cancelarán algunos componentes? En caso afirmativo, no necesitas hacer esas integrales.
7. Determine el campo magnético total, componente por componente, sumando (integrando) los componentes de\(d\vec B\) sobre el cable.

Campo magnético de un cable recto que transporta corriente

En esta sección, utilizamos la Ley Biot-Savart para determinar el campo magnético a una distancia,\(h\), desde el centro de un cable recto finito de longitud,,\(L\) transportando corriente,\(I\), como se ilustra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Configuración del modelo para usar la Ley Biot-Savart para calcular el campo magnético a una\(h\) distancia del centro de un cable portador de corriente de longitud\(L\).

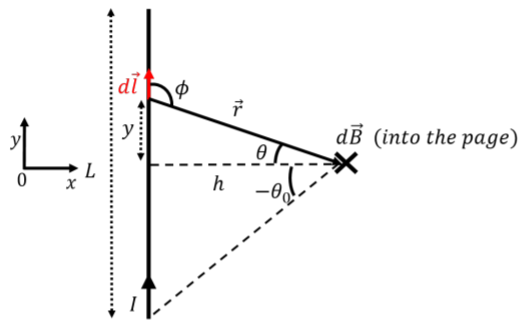
Comenzamos por elegir un elemento infinitesimal de alambre,\(d\vec l\), a una distancia y por encima del centro del alambre, como se muestra (elegimos el origen para que se ubique en el centro del alambre). Por lo tanto,\(d\vec l\) el vector viene dado por:

\[\begin{aligned}d\vec l=dl\hat y \end{aligned}\]

El vector,\(\vec r\), desde\(d\vec l\) el punto en el que nos gustaría conocer el campo magnético viene dado por:

\[\begin{aligned} \vec r&=r\cos\theta\hat x-r\sin\theta\hat y \\ r&=\sqrt{h^{2}+y^{2}}=\frac{h}{\cos\theta} \end{aligned}\]

El producto cruzado entre\(d\vec l\) y\(\vec r\) se encuentra fácilmente con la regla de la derecha para apuntar a la página (correspondiente a la\(z\) dirección negativa). La magnitud del producto cruzado viene dada por:

\[\begin{aligned} ||d\vec l ×\vec r|| = dlr \sin φ \end{aligned}\]

donde\(φ = π/2 + θ\) esta el angulo entre\(d\vec l\) y\(\vec r\), para que\(\sin φ = \cos θ\). Por lo tanto, el producto cruzado puede escribirse en términos de\(θ\) como:

\[\begin{aligned} d\vec l ×\vec r = −dlr \cos θ\hat z \end{aligned}\]

Tenga en cuenta que también podemos determinar el producto cruzado algebraicamente en lugar de usar la regla de la derecha y la magnitud:

\[\begin{aligned} d\vec l\times\vec r &=(dl\vec y)\times (r\cos\theta\hat x-r\sin\theta\hat y) \\ &=dlr\cos\theta(\hat y\times\hat x)-rdl\sin\theta(\hat y\times\hat y) \\ &=-dlr\cos\theta\hat z \end{aligned}\]

El elemento de campo magnético infinitesimal,\(d\vec B\), viene dado por:

\[\begin{aligned} d\vec B=\frac{\mu_{0}I}{4\pi}\frac{d\vec l\times\vec r}{r^{3}}=-\frac{\mu_{0}I}{4\pi}\frac{dl\cos\theta}{r^{2}}\hat z \end{aligned}\]

Cualquier segmento a lo largo del cable dará como resultado un campo magnético que se encuentra en la página (\(z\)dirección negativa), por lo que no habrá cancelaciones debido a ninguna simetría. Ahora podemos proceder a realizar la integral.

Podemos usar cualquiera\(θ\) o\(y\) para etiquetar los elementos de alambre y llevar a cabo la integración. Vamos a optar por integrarnos sobre\(θ\), requiriendo que expresemos\(dl\) y\(r\) en términos de\(θ\) (y constantes), ya que esas son las únicas cantidades en\(d\vec B\) que dependen de la posición de\(d\vec l\). Para expresar\(dl\) en términos de\(dθ\), primero nos referimos\(θ\) a\(y\), la posición del elemento de alambre:

\[\begin{aligned}y=h\tan\theta \rightarrow dl=dy=\frac{dy}{d\theta}d\theta = \frac{h}{\cos ^{2}\theta}d\theta \end{aligned}\]

y\(r\) está dada por:

\[\begin{aligned} r=\frac{h}{\cos\theta}\rightarrow\frac{1}{r^{2}}=\frac{\cos ^{2}\theta}{h^{2}} \end{aligned}\]

Poniendo esto en conjunto en\(d\vec B\):

\[\begin{aligned} d\vec B=-\frac{\mu_{0}I}{4\pi}\frac{dl\cos\theta}{r^{2}}\hat z =-\frac{\mu_{0}I}{4\pi}\left( \frac{h}{\cos ^{2}\theta}d\theta\right)\left(\frac{\cos ^{2}\theta}{h^{2}}\right)\cos\theta\hat z=-\frac{\mu_{0}I}{4\pi h}\cos\theta d\theta\hat z=dB_{z}\hat z \end{aligned}\]

Definimos el ángulo,\(θ_{0}\), para que sea la amplitud máxima del ángulo\(θ\) al integrarse sobre el cable (ver Figura\(\PageIndex{2}\)), de manera que integremos\(θ\) de\(−θ_{0}\) a\(+θ_{0}\):

\[\begin{aligned} B_{z}=\int_{-\theta_{0}}^{+\theta_{0}} dB_{z}=-\frac{\mu_{0}I}{4\pi h}\int_{-\theta_{0}}^{+\theta_{0}}\cos\theta d\theta =-\frac{\mu_{0}I}{4\pi h}(2\sin\theta_{0})=-\frac{\mu_{0}I}{2\pi h}\sin\theta_{0} \end{aligned}\]

Usando las dimensiones dadas:

\[\begin{aligned} \sin\theta_{0}=\frac{L/2}{\sqrt{h^{2}+\frac{L^{2}}{4}}} \end{aligned}\]

Así, el campo magnético\(\vec B\), a una distancia,\(h\), desde el centro de un alambre de longitud,\(L\), que transporta corriente,\(I\), en la\(y\) dirección positiva viene dado por:

\[\vec B=-\frac{\mu_{0}I}{2\pi h}\frac{L/2}{\sqrt{h^{2}+\frac{L^{2}}{4}}}\quad\text{(finite wire)}\]

El campo magnético debe ser rotacionalmente simétrico; es decir, si el cable es vertical, el campo magnético a una distancia h debe verse igual independientemente del ángulo desde el que veamos el cable vertical (siempre debemos ver el campo magnético entrando en la página en el punto que usamos en la Figura\(\PageIndex{2}\)). Así, las líneas del campo magnético deben formar círculos alrededor del alambre, como se ilustra en la Figura\(\PageIndex{3}\). Tenga en cuenta que la dirección del campo magnético viene dada por la regla de la derecha para vectores axiales; cuando alinea su pulgar con la corriente, sus dedos se curvan en la dirección del campo magnético.

Figura\(\PageIndex{3}\): El campo magnético de un cable portador de corriente forma círculos concéntricos centrados en el alambre.

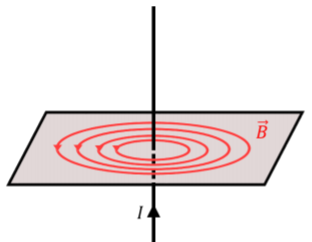
Es de particular interés investigar el caso limitante de un cable infinitamente largo, en el límite de\(L → ∞\), o equivalentemente,\(θ_{0} → \frac{π}{2}\). Este último es más fácil de evaluar, ya que\(\sin θ_{0} → 1\). La magnitud del campo magnético\(\vec B\), una distancia\(h\), desde un cable infinito que transporta corriente\(I\), viene dada por:

\[B=\frac{\mu_{0}I}{2\pi h}\quad\text{(infinite wire)}\]

A menudo se puede hacer la aproximación de que el cable es infinito en longitud, cuando la distancia,\(h\), es pequeña en comparación con la longitud\(L\),, del cable.

Campo magnético de un cable circular portador de corriente

En esta sección, examinamos el campo magnético que es creado por un bucle circular de alambre portador de corriente. Podemos determinar la forma del campo magnético, considerando pequeñas secciones como alambres rectos, con líneas circulares de campo magnético alrededor de ellas. A medida que nos acercamos al centro del anillo, esos campos se suman, como se ilustra en la Figura\(\PageIndex{4}\). Tenga en cuenta que el campo magnético de un bucle de corriente es idéntico al de un imán de barra (como un imán de barra es, por supuesto, una colección de bucles de corriente).

Figura\(\PageIndex{4}\): El campo magnético de un bucle de cable portador de corriente se puede considerar como la suma de los campos de pequeñas secciones rectas de alambre.

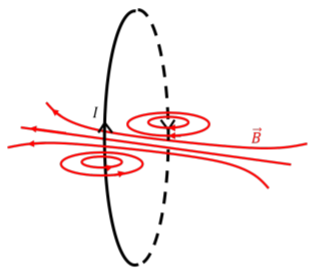
A continuación, utilizamos la Ley Biot-Savart para derivar una expresión para la magnitud del campo magnético a una distancia,\(h\), desde el centro de un anillo de radio,\(R\), a lo largo de su eje de simetría, cuando hay una corriente,\(I\), en el anillo. Si bien las matemáticas son mucho más fáciles que el caso del alambre recto, ¡el reto en este caso es visualizar el cálculo en tres dimensiones! La figura\(\PageIndex{5}\) muestra el bucle de corriente, así como nuestra elección del sistema de coordenadas (con el origen en el centro del anillo). En particular, deseamos calcular el campo magnético a una distancia,\(h\), a lo largo del\(z\) eje. El\(x\) eje entra en la página.

Figura\(\PageIndex{5}\): Diagrama para aplicar la Ley Biot-Savart con el fin de determinar el campo magnético a lo largo del eje de simetría de un anillo que transporta corriente,\(I\). El\(x\) eje entra en la página.

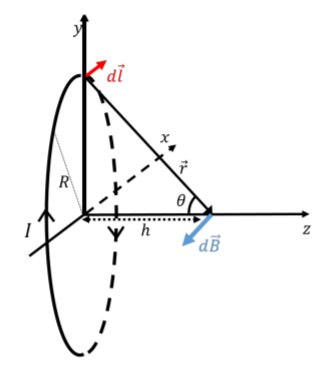
Para aplicar la Ley Biot-Savart, elegimos un elemento,\(d\vec l\), de alambre en la parte superior del anillo, como se ilustra. En esta posición, el elemento,\(d\vec l\), apunta en la\(x\) dirección positiva (hacia la página):

\[\begin{aligned} d\vec l=dl\hat x \end{aligned}\]

El vector,\(\vec r\), desde el elemento de alambre hasta el punto donde deseamos determinar el campo magnético viene dado por:

\[\begin{aligned}\vec r=-r\sin\theta\hat y+r\cos\theta\hat z \end{aligned}\]

y el ángulo\(θ\) será el mismo para todos los elementos de alambre a lo largo del anillo. El producto cruzado,\(d\vec l ×\vec r\), se puede evaluar algebraicamente:

\[\begin{aligned} d\vec l\times\vec r&=(dl\hat x)\times(-r\sin\theta\hat y+r\cos\theta\hat z) \\ &=-rdl\sin\theta(\hat x\times\hat y)+rdl\cos\theta (\hat x\times\hat z) \\ &=-rdl\sin\theta\hat z +rdl\cos\theta (-\hat y) \\ &=-rdl\sin\theta\hat z-rdl\cos\theta\hat y \end{aligned}\]

de manera que el elemento de campo magnético,\(d\vec B\), correspondiente a esa elección de\(d\vec l\), se encuentre en el\(y − z\) plano, como se ilustra en la Figura\(\PageIndex{5}\). Obsérvese que el vector\(d\vec B\) es perpendicular al vector\(\vec r\) (ya que es el producto cruzado de\(\vec r\) con otro vector). El elemento de campo magnético,\(d\vec B\), viene dado por:

\[\begin{aligned} d\vec B&=\frac{\mu_{0}I}{4\pi}\frac{d\vec l\times\vec r}{r^{3}}=\frac{\mu_{0}I}{4\pi r^{3}}(-rdl\sin\theta\hat z-rdl\cos\theta\hat y) \\ &=\frac{\mu_{0}I}{4\pi r^{2}}(-dl\sin\theta\hat z-dl\cos\theta\hat y)=dB_{z}\hat z+dB_{y}\hat y \end{aligned}\]

A medida que el elemento de alambre\(d\vec l\),, se mueve alrededor del círculo, la punta del elemento vectorial de campo magnético resultante traza un círculo centrado en el\(z\) eje, como se ilustra en la Figura\(\PageIndex{6}\). Obsérvese que, en general, también\(d\vec B\) tendrá un\(x\) componente. De esta manera, solo el\(z\) componente del campo magnético no se cancelará cuando sumemos juntos los elementos del campo magnético que provienen de los diferentes elementos de alambre.

Figura\(\PageIndex{6}\): A medida que el elemento de alambre\(d\vec l\),, se mueve a lo largo del anillo, la punta del vector de elemento de campo magnético correspondiente\(d\vec B\),, describe un círculo centrado en el\(z\) eje. Por lo tanto, solo el\(z\) componente (negativo) de\(d\vec B\) sobrevivirá cuando todos estos se sumen.

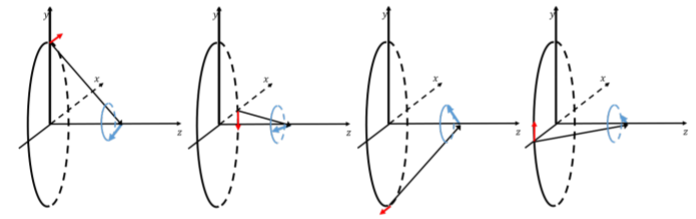
El campo magnético total estará en la\(z\) dirección negativa, como se anticipa de la Figura\(\PageIndex{4}\). Sumando los\(z\) componentes de los campos magnéticos infinitesimales:

\[\begin{aligned} dB_{z}&=-\frac{\mu_{0}I}{4\pi r^{2}}dl\sin\theta \\ B_{z}&=\int dB_{z}=-\int \frac{\mu_{0}I}{4\pi r^{2}}dl\sin\theta \end{aligned}\]

Tenga en cuenta que en este caso, ambos\(r\) y\(θ\) son constantes para todos los\(d\vec l\), permitiéndonos sacarlos de la integral. La integral es entonces solo una suma de los elementos dl, que deben sumar hasta la circunferencia del anillo:

\[\begin{aligned} B_{z}=\int dB_{z}=-\frac{\mu_{0}I}{4\pi r^{2}}\sin\theta \int_{0}^{2\pi R}dl =-\frac{\mu_{0}I}{4\pi r^{2}}\sin\theta (2\pi R)=-\frac{\mu_{0}I}{2r^{2}}R\sin\theta \end{aligned}\]

En cuanto a las variables que se nos dan:

\[\begin{aligned} r&=\sqrt{R^{2}+h^{2}} \\ \sin\theta &=\frac{R}{r}=\frac{R}{\sqrt{R^{2}+h^{2}}} \end{aligned}\]

\[\therefore\vec B=-\frac{\mu_{0}I}{2}\frac{R^{2}}{(R^{2}+h^{2})^{\frac{3}{2}}}\hat z\quad\text{(field from a loop of current)}\]

En este caso, la matemática fue relativamente sencilla (sin sustituciones para evaluar la integral), sin embargo es un reto visualizar el problema en tres dimensiones.

Ejercicio\(\PageIndex{1}\)

Una bobina está hecha de\(N\) bucles de alambre portador de corriente empaquetados estrechamente juntos. ¿Cuál es el campo magnético en el centro de la bobina?

1. \(\frac{µ_{0}I}{2R}\)
2. \(\frac{Nµ_{0}I}{2R}\)
3. \(\frac{Nµ_{0}I}{2R^{2}}\)
4. \(\frac{µ_{0}I}{R}\)

Contestar