24.6: Transformaciones de Lorentz y espacio-tiempo

Espacio-tiempo de cuatro dimensiones

Hasta el momento, hemos visto que nuestras nociones de intervalos de tiempo (el tiempo entre dos eventos) e intervalos espaciales (la distancia entre dos ubicaciones) dependen de nuestro marco de referencia. También vimos cómo el espacio y el tiempo están conectados, por ejemplo, por el hecho de que la dilatación del tiempo debe ir de la mano con la contracción de la longitud. También concluimos que no existe un concepto absoluto de tiempo, y que el tiempo es relativo (depende de su marco de referencia).

En el contexto de la Relatividad Especial, introducimos el concepto de espacio-tiempo. Para describir la ubicación de un objeto en el espacio-tiempo, debemos especificar tanto las coordenadas de ubicación/posición (\(x\),\(y\),\(z\)) como la “coordenada” de tiempo,\(t\). Dado que el tiempo\(t\),, tiene la dimensión del tiempo, solemos especificar la coordenada de tiempo multiplicándola por la velocidad de la luz\(ct\),, para que tenga dimensiones de longitud. Así, la posición en el espacio-tiempo viene dada por 4 coordenadas:\((x,y,z,ct)\).

Diagramas espacio-tiempo

Es prácticamente imposible visualizar situaciones en tres dimensiones, ¡así que cuatro dimensiones son desesperadas! Sin embargo, podemos obtener mucha información sobre los modelos de Relatividad Especial mediante el uso de “diagramas de espacio-tiempo”. En un diagrama de espacio-tiempo, utilizamos solo una de las coordenadas del espacio (normalmente\(x\)) junto con la coordenada de tiempo,\(ct\), para definir los dos ejes de un diagrama de espacio-tiempo. Los diagramas espacio-tiempo son análogos a los gráficos de “posición en función del tiempo” que se dibujarían en cinemática, aunque son fundamentalmente diferentes en que, para un diagrama de espacio-tiempo, las coordenadas deben ser pensadas como independientes (no se está trazando una variable dependiente en función de una independiente variable).

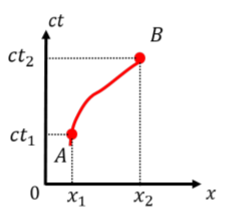
La figura\(\PageIndex{1}\) muestra un diagrama espacio-tiempo para un objeto que se ubicó en la posición\(x=x_1\) en el tiempo\(t=t_1\) (ubicación\(A\)), y en la posición\(x=x_2\) en el tiempo\(t=t_2\) (ubicación\(B\)). El camino de un objeto a través del espacio-tiempo, indicado por la línea que conecta\(A\) y\(B\), se llama la “línea mundial” del objeto.

Figura\(\PageIndex{1}\): Línea mundial de un objeto que se movió de ubicaciones\(A\) en el espacio-tiempo a la ubicación\(B\) en el espacio-tiempo.

Ejercicio\(\PageIndex{1}\)

¿Qué aspecto tiene la línea mundial de una partícula estacionaria?

1. Una línea vertical.
2. Una línea horizontal.
3. Un punto.

Contestar

Un pulso de luz viajando en la\(x\) dirección siempre tendrá una línea mundial que hace un\(45^{\circ}\) ángulo con el eje horizontal (espacio) (ya que\(x=ct\)). La línea mundial de cualquier objeto que viaje con una velocidad por debajo de la velocidad de la luz siempre debe hacer un ángulo con el eje horizontal que sea mayor que\(45^{\circ}\).

Una posición en el espacio-tiempo suele llamarse “evento”. Podemos dibujar un conjunto de líneas, a\(45^{\circ}\) grados del eje horizontal, que se cruzan en un evento en el espacio-tiempo. Esas líneas definen dos “conos de luz” correspondientes a: (1) ubicaciones en el espacio-tiempo en el pasado que podrían haber tenido un efecto causal sobre el evento (el “cono de luz pasado”), y (2), ubicaciones en espacio-tiempo en el futuro para las cuales el evento puede tener un efecto causal (el “cono de luz futuro”).

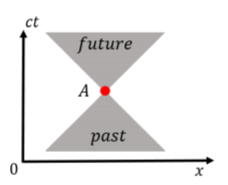
La figura\(\PageIndex{2}\) muestra los conos de luz asociados a un evento,\(A\), en el espacio-tiempo. El cono de luz pasado es la única región del espacio-tiempo en la que un evento diferente podría haber impactado en el evento\(A\). Por ejemplo, el evento\(A\) podría ser que “el objeto está en posición\(x=x_1\) en el tiempo\(t=t_1\)”, de manera que el cono de luz pasado corresponde a las únicas ubicaciones en el espacio-tiempo que el objeto podría haber estado en el pasado. Del mismo modo, el futuro cono de luz define las ubicaciones en el espacio-tiempo sobre las cuales el evento\(A\) podría tener un efecto. Por ejemplo, esto podría definir las posibles ubicaciones del objeto en el futuro. Las regiones fuera de los conos de luz nunca pueden tener un efecto sobre el evento\(A\); no están conectadas causalmente. Una señal u objeto necesitaría viajar más rápido que la velocidad de la luz para tener un efecto en algo fuera de su cono de luz. Hay ubicaciones en el espacio-tiempo, en el futuro de nuestro Universo, en las que no podemos influir, no importa lo que hagamos.

Figura\(\PageIndex{2}\): Los conos de luz pasados y futuros asociados con el evento espacio-tiempo,\(A\).

Cuando dos eventos en el espacio-tiempo están dentro de los conos de luz del otro, decimos que el intervalo espacio-tiempo entre ellos (la línea que dibujas de un evento a otro) es “similar al tiempo”. Los eventos similares al tiempo son tales que todos los observadores, en cualquier marco de referencia, estarán de acuerdo en que un evento ocurrió antes que el otro. Así, los eventos que están relacionados causalmente deben tener un intervalo similar al tiempo entre ellos (están conectados por una línea que hace un ángulo mayor que\(45^{\circ}\) con el eje horizontal).

Se dice que dos eventos que están fuera de los conos de luz del otro son “parecidos al espacio”. Los eventos que están conectados por intervalos similares al espacio no pueden estar relacionados causalmente (uno no puede causar el otro). Los observadores en diferentes marcos de referencia no estarán de acuerdo sobre el orden temporal de eventos similares al espacio. Por ejemplo, cuando Alice observó los dos relojes en la plataforma para emitir pulsos de luz al mismo tiempo, Brice no estuvo de acuerdo; esos dos eventos están conectados por un intervalo similar al espacio.

Finalmente, se dice que el intervalo espacio-tiempo entre eventos que están en el cono de luz del otro (conectados por una línea que forma un\(45^{\circ}\) ángulo con el eje x), es “parecido a la luz” o “nulo”.

Transformaciones de Lorentz

En esta sección, consideramos cómo transformar las coordenadas espacio-tiempo\((x,y,z,ct)\), como se mide en un marco de referencia,\(S\), para coordinar\((x',y',z',c't)\), como se mide en un marco de referencia,\(S'\), que se mueve con una velocidad constante, \(v\), relativo al marco,\(S\). Por simplicidad, asumimos que el marco\(S'\) se mueve con velocidad\(v\) en la\(x\) dirección positiva, medida en marco\(S\), y que el origen de los dos sistemas de coordenadas coincidió en el momento\(t=0\). La figura\(\PageIndex{3}\) muestra una ilustración de cómo se relacionan los dos marcos de referencia (nótese que estos son sistemas de coordenadas reales, no diagramas espacio-tiempo).

Figura\(\PageIndex{3}\): El marco de referencia\(S'\) se mueve en relación con el marco de referencia\(S\),, con velocidad\(v\) en la\(x\) dirección. En su momento\(t = 0\) coincidieron los orígenes de los dos sistemas de coordenadas.

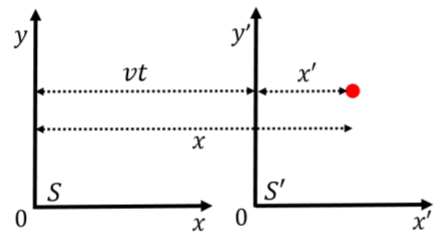
Si ignoramos alguna de la Relatividad Especial, entonces las coordenadas en\(S'\) se relacionan fácilmente con las del\(S\) marco de referencia usando las “transformaciones galileanas”:\[\begin{aligned} x' &= x - vt\\ y' &= y\\ z' &= z\\ t' &= t\end{aligned}\] y esto corresponde a transformaciones que hemos utilizado implícitamente antes de considerar Especial Relatividad. Estas ecuaciones también nos permiten relacionar las velocidades medidas en diferentes marcos de referencia. Supongamos que un objeto tiene una velocidad\(\vec u=(u_x,u_y,u_z)\), como se mide en el marco de referencia,\(S\). Podemos obtener los componentes del vector de velocidad\(\vec u'\), como se mide en el marco de referencia,\(S'\), tomando las derivadas de tiempo de las ecuaciones anteriores:\[\begin{aligned} u'_x &= \frac{dx'}{dt'}=\frac{dx'}{dt}=\frac{d}{dt}(x-vt)=\frac{dx}{dt}-v=u_x - v\\ u'_y &=\frac{dy'}{dt'}=u_y\\ u'_z &=\frac{dz'}{dt'}=u_z\end{aligned}\] que es trivial, ya que\(t=t'\). Las transformaciones anteriores son equivalentes (idénticas) a las reglas para la velocidad de transformación que derivamos en la Sección 3.4 para cinemática. En la relatividad galilea, el tiempo es una cantidad absoluta que no depende del marco de referencia. En Relatividad Especial, la coordenada de tiempo es diferente entre diferentes marcos de referencia, por lo que no podemos simplemente convertir una derivada de tiempo en\(t'\) una derivada en\(t\). En cambio, debemos usar las transformaciones de Lorentz.

Podemos usar las fórmulas de contracción de longitud y dilatación de tiempo para derivar las Transformaciones de Lorentz. Haciendo referencia a la Figura\(\PageIndex{3}\),\(x\) se refiere a la distancia entre un punto en el espacio-tiempo y el origen del\(x\) eje en el fotograma\(S\),, medida en fotograma,\(S\). De igual manera\(x'\),, es la distancia al punto en espacio-tiempo medida en fotograma\(S'\), desde el origen de\(S'\). En marco,\(S\), la distancia\(x'\) se contrae a la longitud\(x'/\gamma\), de manera que la transformación galileana para la\(x\) coordenada se modifica de la siguiente manera:\[\begin{aligned} x' &= x - vt\quad\text{(Galilean)}\\ \frac{x'}{\gamma} &= x - vt\\ \therefore x'&=\gamma (x-vt)\quad\text{(Lorentz)}\end{aligned}\] La\(y\) y\(z\) las coordenadas son las mismas entre fotogramas de referencias, ya que toda la contracción de longitud se llevará a cabo en la dirección del movimiento relativo entre fotogramas de referencia, que elegimos estar en la\(x\) dirección.

Podemos obtener la ecuación para la coordenada temporal considerando que, en el\(S'\) marco de referencia, es la\(x\) coordenada a la que se contrae\(x/\gamma\). En el\(S'\) marco de referencia, la distancia entre los orígenes de los dos sistemas es\(vt'\) (tenga en cuenta el prime on\(t\)). Podemos así escribir la distancia contraída\(x\), en el\(S'\) marco de referencia:\[\begin{aligned} \frac{x}{\gamma}&=vt'+x'\\ t'&= \frac{1}{v}\left(\frac{x}{\gamma}-x'\right)\end{aligned}\] Podemos eliminar\(x'\) de la última ecuación usando la transformación de Lorentz para la\(x'\) que acabamos de encontrar:\[\begin{aligned} t'&= \frac{1}{v}\left(\frac{x}{\gamma}-x'\right)\\ t'&= \frac{1}{v}\left(\frac{x}{\gamma}-\gamma x+\gamma vt\right)\\ \frac{t'}{\gamma}&=\frac{1}{v}\left(\frac{x}{\gamma^2}-x+vt\right)\\ &=\frac{1}{v}\left(x\left(1-\frac{v^2}{c^2}\right)-x+vt\right)\\ &=\frac{1}{v}\left(-\frac{v^2}{c^2}x+vt\right)\\ &=t-\frac{vx}{c^2}\\ \therefore t'&=\gamma\left(t-\frac{vx}{c^2} \right)\end{aligned}\] donde escribimos fuera el\(\gamma\) factor fuera explícitamente en la cuarta línea. Podemos resumir las transformaciones de Lorentz de la siguiente manera:\[\begin{aligned} x' &=\gamma (x-vt)\\ y' &= y\\ z' &= z\\ t' &=\gamma\left(t-\frac{vx}{c^2} \right)\end{aligned}\] y las relaciones inversas se encuentran fácilmente:\[\begin{aligned} x &=\gamma (x'+vt')\\ y &= y'\\ z &= z'\\ t &=\gamma\left(t'+\frac{vx'}{c^2} \right)\end{aligned}\] Obsérvese que las transformaciones de Lorentz reducen a las transformaciones galileanas cuando la velocidad\(v\),, entre marcos de referencia es pequeña (de manera que \(\gamma \sim 1\)).

Ejemplo\(\PageIndex{1}\)

En un marco,\(S\), a pulse of light is emitted (at the speed of light) in the positive \(x\) direction, at \(t=0\), from the origin. The pulse is then absorbed at time \(t\), at position \(x=d\). Use the Lorentz transformation to show that, in a frame, \(S'\), moving in the positive \(x\) direction with speed \(v\), relative to \(S\), the pulse also traveled at the speed of light.

Solución:

Para poder utilizar las transformaciones de Lorentz, necesitamos definir “eventos”, con coordenadas en espacio-tiempo, que luego podamos convertir de un marco de referencia a otro. \(A\)Sea el evento que corresponde a la emisión del pulso de luz, y\(B\) el evento que corresponde a la absorción del pulso. En frame,\(S\), las coordenadas de estos eventos son:\[\begin{aligned} x_A&=0\\ t_A&=0\\ x_B&=d\\ t_B&=\frac{d}{c}\end{aligned}\] donde en la última línea, utilizamos el hecho de que, en frame\(S\), el pulso viaja a la velocidad de la luz. Aplicando las transformaciones de Lorentz, podemos encontrar las coordenadas de los mismos eventos en cuadro,\(S'\):\[\begin{aligned} x'_A&=\gamma (x_A-vt_A)=0\\ t'_A&=\gamma\left(t_A-\frac{vx_A}{c^2} \right)=0\\ x'_B&=\gamma (x_B-vt_B)=\gamma \left(d-v\frac{d}{c}\right)\\ t'_B&=\gamma\left(t_B-\frac{vx_B}{c^2} \right)=\gamma\left(\frac{d}{c}-\frac{vd}{c^2} \right)\end{aligned}\] La velocidad,\(v'_p\), del pulso de luz en cuadro,\(S'\), viene dada por:\[\begin{aligned} v'_p&=\frac{(x'_B-x'_A)}{(t'_B-t'_A)}=\frac{\gamma \left(d-v\frac{d}{c}\right)}{\gamma\left(\frac{d}{c}-\frac{vd}{c^2} \right)}\\ &=\frac{\left(d-v\frac{d}{c}\right)}{\left(\frac{d}{c}-\frac{vd}{c^2} \right)}=c\frac{\left(\frac{d}{c}-v\frac{d}{c^2}\right)}{\left(\frac{d}{c}-\frac{vd}{c^2} \right)}=c\end{aligned}\] que es la velocidad de la luz, como se esperaba.

Discusión:

En este ejemplo, mostramos cómo utilizar las transformaciones de Lorentz, definiendo claramente los “eventos” y sus coordenadas en el espacio-tiempo. Vimos que la transformación de Lorentz son consistentes con el segundo postulado de Einstein y que la velocidad de la luz es la misma todos los marcos de referencia. Esto por supuesto tiene sentido, ya que derivamos las transformaciones de Lorentz a partir de la dilatación del tiempo y la contracción de la longitud, que son consecuencias del postulado.

El segundo postulado de Einstein establece que la velocidad de la luz es independiente del marco de referencia. Considera dos puntos en el espacio-tiempo correspondientes a la emisión (\(A\)) y la absorción (\(B\)) de un pulso de luz. En el marco de referencia\(S\),, la distancia al cuadrado en el espacio entre estos dos eventos debe ser igual a la distancia (cuadrada) que recorrió la luz entre el tiempo de emisión y absorción:\[\begin{aligned} (x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2&= c^2(t_B-t_A)^2\\ \therefore \Delta x^2 + \Delta y^2 +\Delta z^2&=c^2\Delta t^2\end{aligned}\] dónde\((x_A,y_A,z_A,ct_A)\) y\((x_B,y_B,z_B,ct_B)\) son las coordenadas espacio-tiempo de eventos\(A\) y\(B\). La ecuación anterior debe mantenerse en todos los marcos de referencias (por ejemplo, agregar un primo a cada coordenada), ya que es una declaración de que la velocidad de la luz es\(c\).

Podemos definir,\(s\), el” intervalo espacio-tiempo”, entre eventos,\(A\) y\(B\):\[\begin{aligned} s^2 = \Delta x^2 + \Delta y^2 +\Delta z^2&-c^2\Delta t^2\end{aligned}\] que resulta ser “Lorentz invariante” (es decir, que este valor es el mismo en todos los marcos de referencia). El intervalo espacio-tiempo puede pensarse como una “distancia” en el espacio-tiempo que es la misma en todos los marcos de referencia. Si los eventos\(A\) y\(B\) corresponde a la emisión y absorción de luz, entonces\(s=0\), y decimos que el intervalo entre\(A\) y\(B\) es parecido a la luz o nulo. Si\(s<0\), los eventos están en un intervalo similar al tiempo, y si\(s>0\), los eventos están separados por un intervalo similar al espacio. Dado que\(s\) no depende del marco de referencia, todos los observadores acordarán si los eventos están separados por intervalos temporales o espaciales.

Podemos visualizar el efecto de las transformaciones de Lorentz en diagramas espacio-tiempo, como en la Figura\(\PageIndex{4}\), que muestra los diagramas espacio-tiempo para un marco de referencia,\(S\), y un segundo marco de referencia,\(S'\), moviéndose con velocidad\(v\) en el \(x\)dirección relativa a\(S\).

Figura\(\PageIndex{4}\): El marco de referencia\(S'\) se mueve en relación con el marco de referencia\(S\),, con velocidad\(v\) en la\(x\) dirección. Podemos ilustrar esto en un diagrama espacio-tiempo inclinando los ejes del sistema de\(S'\) coordenadas en un ángulo tan\(α = v/c\), como se muestra.

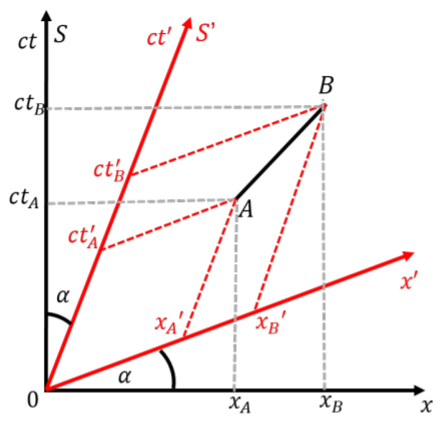
El efecto de la transformación de Lorentz en un diagrama espacio-tiempo es inclinar tanto los ejes de espacio como de tiempo “hacia adentro” ¹, por un ángulo\(\alpha\), dado por:\[\begin{aligned} \tan\alpha = \frac{v}{c}\end{aligned}\] La figura\(\PageIndex{4}\) muestra un intervalo similar a la luz entre dos puntos,\(A\) y \(B\), y cómo determinar las coordenadas espacio-tiempo en los dos marcos de referencia. Se puede pensar en el espacio-tiempo como la hoja de papel en la que ocurren los eventos. Luego puede dibujar diferentes sistemas de coordenadas en esa hoja de papel para describir la posición (en el espacio y el tiempo) de diferentes eventos.

Ejemplo\(\PageIndex{2}\)

Utilice un diagrama de espacio-tiempo para mostrar cómo dos eventos en diferentes ubicaciones que son simultáneos en un marco de referencia no son simultáneos en un marco de referencia que se mueve en relación con aquel en el que los eventos son simultáneos. Esto es una ilustración de la relatividad de la simultaneidad que descubrimos al inicio del capítulo al examinar a Alicia en una plataforma de tren y los dos pulsos de luz.

Solución:

\(S\)Sea el marco de referencia donde los eventos,\(A\) y\(B\), son simultáneos. Estos eventos están conectados por un intervalo similar al espacio, ya que están separados en el espacio, pero no en el tiempo. No hay manera de que un evento haya causado al otro. En el marco,\(S\), estos eventos están en una línea horizontal en un diagrama espacio-tiempo.

Definamos un segundo marco de referencia,\(S'\), que se mueve con velocidad\(v\), relativo a\(S\). Hemos ilustrado diagramas espacio-tiempo para los dos marcos de referencia, y los eventos\(A\) y\(B\), en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): En el marco de referencia\(S\),, los eventos\(A\) y\(B\) ocurren al mismo tiempo. En marco,\(S'\), evento\(B\) ocurre antes del evento\(A\) (desde\(t_{B} < t_{A}\)). Los dos eventos son de tipo espacial, por lo que los observadores en diferentes marcos de referencia no pueden ponerse de acuerdo sobre cuál ocurrió primero.

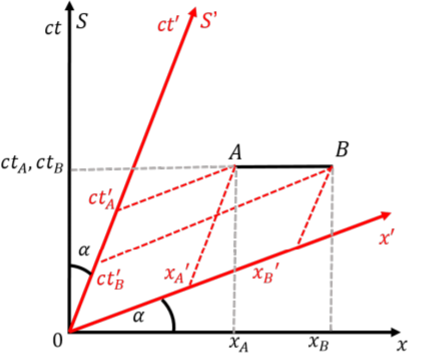
Del diagrama espacio-tiempo, queda claro que, en el marco de referencia\(S'\), el suceso\(B\) ocurrió primero. Si el marco de referencia\(S'\) se moviera en la dirección opuesta (negativa\(x\)), el evento\(A\) ocurriría primero, y los ejes de se\(S'\) inclinarían en la otra dirección (de manera que el ángulo de apertura entre los ejes sea mayor que \(90^{\circ}\)).

Discusión:

Este ejemplo ilustra cómo se pueden usar diagramas de espacio-tiempo para modelar cualitativamente eventos en espacio-tiempo entre dos marcos de referencia diferentes. En particular, mostramos cómo dos eventos que son simultáneos en un fotograma (\(S\)) no son simultáneos en un fotograma diferente. Para los eventos conectados por intervalos similares al espacio, existen marcos de referencia donde los eventos son simultáneos, o donde cualquiera de ellos sucedió primero. Si dos eventos están separados por un intervalo similar al tiempo, no hay marco de referencia en el que uno no esté de acuerdo en el orden de los eventos (aunque los observadores en diferentes marcos de referencia seguirán midiendo diferentes longitudes de tiempo entre eventos debido a la dilatación del tiempo). Para eventos similares al tiempo, el marco de referencia móvil tendría que ir más rápido que la velocidad de la luz para que el orden de tiempo fuera diferente. Esto violaría la causalidad, y es un buen argumento de por qué nada puede ir más rápido que la velocidad de la luz!

Pensamientos de josh

Este capítulo es donde se hace estallar la burbuja de la realidad intuitiva, y a los estudiantes (como tú y yo) se les da la oportunidad de desafiar nuestra comprensión de cómo opera el universo. Por increíble y emocionante que sea esto, también puede ser increíblemente frustrante. Muchos estudiantes confían en la intuición para guiarlos a medida que resuelven problemas, pero chocan contra una pared en relatividad especial. Para evitar este problema, sugiero dibujar diagramas espacio-tiempo y usar transformaciones de Lorentz. Practicar con estas herramientas ayudará a que el proceso de entender las extrañas consecuencias de los postulados de Einstein sea menos incómodo.

Además de los consejos prácticos que he dado, reconozco abrazar la extrañeza de la realidad. A lo largo de la historia, los científicos se han aventurado en lo desconocido en intentos de descubrir y decodificar el universo. En muchos casos, la respuesta a una pregunta ha planteado más preguntas que respuestas, y a la humanidad se le da la oposidad de entender mejor el mundo en el que vivimos. Como estudiante, estás participando en un proceso de comprensión que nos permite continuar con la aventura que es la indagación científica. La confusión puede ser frustrante, pero no dejes que te desanime, ¡estar confundido significa que estás a solo unos pasos de entender!

Adición Lorentz de velocidades

En la sección anterior, revisamos las transformaciones de velocidad galileana, que nos permiten convertir una velocidad\(\vec u\), medida en un marco de referencia, a una velocidad,\(\vec u'\), medida en otro marco de referencia. Ahora derivamos las relaciones equivalentes basadas en la transformación de Lorentz. Nuevamente, asumimos que el marco\(S'\),, se mueve en la\(x\) dirección positiva con la velocidad\(v\),, relativo al marco,\(S\).

El\(x\) componente del vector de velocidad,\(\vec u'\), para algún objeto en el\(S'\) marco de referencia viene dado por:\[\begin{aligned} u'_x = \frac{d}{dt'} x'\end{aligned}\] En la relatividad galilea, podríamos simplemente reemplazar la derivada\(t'\) por una derivada sobre \(t\), ya que los dos son equivalentes. Este ya no es el caso. Sin embargo, podemos usar la Regla de Cadena y las transformaciones de Lorentz para convertir una derivada sobre\(t'\) una derivada sobre\(t\):\[\begin{aligned} \frac{d}{dt'} &= \frac{dt}{dt'}\frac{d}{dt}\\ &= \frac{d}{dt'} \gamma\left(t'+\frac{vx'}{c^2} \right)\frac{d}{dt}\\ &=\gamma \left(1+\frac{v}{c^2}\frac{dx'}{dt'}\right)\frac{d}{dt}\\ &=\gamma \left(1+\frac{vu'_x}{c^2}\right)\frac{d}{dt}\end{aligned}\] donde lo reconocimos\(\frac{dx'}{dt'}=u'_x\). El\(x\) componente de la velocidad, medido en el\(S'\) marco de referencia, viene dado entonces por:\[\begin{aligned} u'_x &= \frac{d}{dt'} x' = \gamma \left(1+\frac{vu'_x}{c^2}\right)\frac{d}{dt}x'\\ &=\gamma \left(1+\frac{vu'_x}{c^2}\right)\frac{d}{dt}\gamma (x-vt)\\ &=\gamma^2 \left(1+\frac{vu'_x}{c^2}\right)(u_x -v)\\ \frac{u'_x}{\gamma^2}&=u_x -v +\frac{vu'_xu_x}{c^2}-\frac{v^2u'_x}{c^2}\\ u'_x\left (1-\frac{v^2}{c^2}\right)&=u_x -v +\frac{vu'_xu_x}{c^2}-\frac{v^2u'_x}{c^2}\\ u'_x \left( 1- \frac{vu_x}{c^2}\right) &=u_x -v \end{aligned}\]

\[\therefore\mu_{x}^{'}=\frac{\mu_{x}-v}{1-\frac{v\mu_{x}}{c^{2}}}\]

donde hicimos uso de la transformación de Lorentz:\(x'=\gamma (x-vt)\). Podemos proceder de manera similar para determinar los\(z\) componentes\(y\) y. Tenga en cuenta que, a diferencia del caso galileo, todos los componentes de velocidad deben transformarse, ya que la derivada de tiempo está involucrada para cada componente. Intuitivamente, esperamos que todos los componentes de la velocidad se vean afectados, ya que se necesita garantizar que la velocidad total esté siempre por debajo\(c\). Las transformaciones de velocidad para todos los componentes vienen dadas por lo siguiente:\[\begin{aligned} u'_x&=\frac{u_x -v}{1- \frac{vu_x}{c^2}}\\ u'_y &=\frac{u_y}{\gamma\left(1- \frac{vu_x}{c^2}\right)}\\ u'_z &=\frac{u_z}{\gamma\left(1- \frac{vu_x}{c^2}\right)}\end{aligned}\] y las transformaciones inversas están dadas por:\[\begin{aligned} u_x &=\frac{u'_x +v}{1+ \frac{vu_x}{c^2}}\\ u_y &=\frac{u'_y}{\gamma\left(1+ \frac{vu_x}{c^2}\right)}\\ u_z &=\frac{u'_z}{\gamma\left(1+ \frac{vu_x}{c^2}\right)}\end{aligned}\]

Ejemplo\(\PageIndex{3}\)

Un arquero puede disparar una flecha muy rápida con una velocidad de\(0.5c\). The archer is on a train moving with speed, \(v=0.7c\), and fires an arrow in the direction of motion. What is the speed of the arrow, as measured in the frame of reference of the ground?

Solución:

Que el tren sea el marco de referencia,\(S'\), moviéndose en la\(x\) dirección positiva con la velocidad\(v=0.7c\) relativa al marco\(S\),, que corresponde al suelo. La velocidad de la flecha, vista desde el tren (\(S'\)), viene dada por:\[\begin{aligned} u'_x = 0.5c\end{aligned}\] La velocidad de la flecha, medida desde el suelo, viene dada por:\[\begin{aligned} u_x &=\frac{u'_x +v}{1+ \frac{vu_x}{c^2}}\\ &=\frac{(0.5c) +(0.7c)}{1+ \frac{(0.7c)(0.5c)}{c^2}}\\` &=\frac{(1.2c)}{1+(0.7)(0.5)}=\frac{1.2}{1.35}c=0.89c\end{aligned}\]

Discusión:

Al utilizar las transformaciones de Lorentz para la velocidad, vemos que la flecha no supera la velocidad de la luz. Si hubiéramos usado la relatividad galileana, habríamos llegado a la conclusión de que la flecha tiene una velocidad de\(1.2c\) cuando se mide desde el suelo.

Notas al pie

1. Hacia afuera si la velocidad de\(S'\) está en la\(x\) dirección negativa relativa a\(S\).