25.1: Sistemas de coordenadas

Los sistemas de coordenadas se utilizan para describir la posición de un objeto en el espacio. Un sistema de coordenadas es una herramienta matemática artificial que construimos para describir la posición de un objeto real.

Sistemas de coordenadas 1D

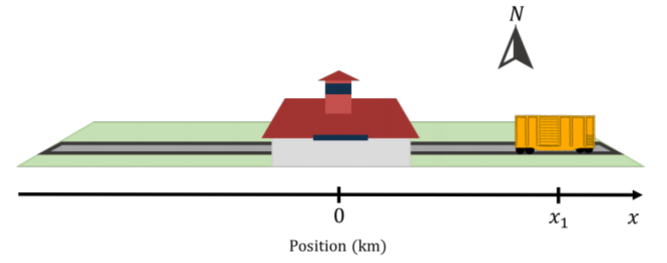
El sistema de coordenadas más fácil de construir es uno que podemos usar para describir la ubicación de los objetos en el espacio unidimensional. Por ejemplo, es posible que deseemos describir la ubicación de un tren a lo largo de una sección recta de vía que discurre en dirección Este-Oeste. Para ello, primero debemos definir un “origen”, que es el punto de referencia de nuestro sistema de coordenadas. Por ejemplo, el origen de nuestra vía de tren puede ser la estación de tren de Kingston (Figura A1.1.1).

Podemos describir la posición del tren especificando qué tan lejos está de la estación de tren (el origen), utilizando un solo número real, digamos\(x\). Si el tren está en posición\(x=0\), entonces sabemos que está en la estación Kingston. Si el objeto no está en el origen, entonces necesitamos poder especificar en qué lado (Este u Oeste en nuestro ejemplo de tren) del origen se encuentra el objeto. Esto lo hacemos eligiendo una dirección para nuestra coordenada unidimensional\(x\). Por ejemplo, podemos elegir que el lado Este de la pista corresponda a valores positivos de\(x\) y que el lado Oeste de la pista corresponda a los valores negativos de\(x\). Por lo tanto, para especificar completamente un sistema de coordenadas unidimensional tenemos que elegir:

• la ubicación del origen.
• la dirección en la que la coordenada,\(x\), aumenta.
• las unidades en las que deseamos expresar\(x\).

En una dimensión, es común utilizar la variable para definir la posición\(x\) a lo largo del “\(x\)-eje”. El\(x\) eje -es nuestro sistema de coordenadas en una dimensión, y lo representamos dibujando una línea con una flecha en dirección de incremento\(x\) e indicamos dónde se encuentra el origen (como en la Figura A1.1.1).

Figura A1.1.1: Un sistema de coordenadas 1d que describe la posición de un tren. La estación de tren de Kingston es el origen y el lado este de la vía corresponde a valores positivos de\(x\). El tren se encuentra en posición\(x_{1}\).

Sistemas de coordenadas 2D

Figura A1.1.2: Ejemplo de sistema de coordenadas cartesianas y un punto\(P\) con coordenadas\((x_{p}, y_{p})\).

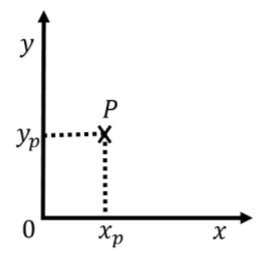
Para describir la posición de un objeto en dos dimensiones (por ejemplo, una canica rodando sobre una mesa), necesitamos especificar dos números. La forma más fácil de hacerlo es definir dos ejes,\(x\) y\(y\), cuyo origen y dirección debemos definir. La Figura A1.1.2 muestra un ejemplo de dicho sistema de coordenadas. Si bien no es necesario hacerlo, elegimos\(x\) y\(y\) ejes que son perpendiculares entre sí. El origen del sistema de coordenadas es donde se cruzan los dos ejes. Uno es libre de elegir dos direcciones cualesquiera para los ejes (siempre y cuando no sean paralelos). Sin embargo, elegir ejes que sean perpendiculares (un sistema de coordenadas “cartesianas”) suele ser lo más conveniente.

Para describir completamente la posición de un objeto, debemos especificar tanto su posición a lo largo de\(x\) los\(y\) ejes como. Por ejemplo, el punto\(P\) en la Figura A1.1.2 tiene dos coordenadas,\(x_p\) y\(y_p\), que definen su posición. La\(x\) coordenada se encuentra dibujando una línea a través\(P\) de la cual es paralela al\(y\) eje y viene dada por la intersección de esa línea con el\(x\) eje. La\(y\) coordenada se encuentra dibujando una línea a través del punto\(P\) que es paralelo al\(x\) eje y viene dada por la intersección de esa línea con el\(y\) eje.

Ejercicio\(\PageIndex{1}\)

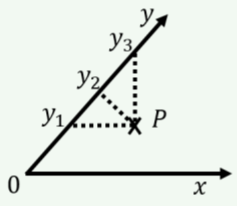
La Figura A1.1.3 muestra un sistema de coordenadas que no es ortogonal (donde los\(y\) ejes\(x\) y no son perpendiculares). ¿Qué valor en la figura indica correctamente la\(y\) coordenada del punto\(P\)?

Figura A1.1.3: Un sistema de coordenadas no ortogonales (los\(y\) ejes\(x\) y no son perpendiculares).

1. \(y_1\)
2. \(y_2\)
3. \(y_3\)

Responder

Agrega textos aquí. No elimine primero este texto.

La elección más común del sistema de coordenadas en dos dimensiones es el sistema de coordenadas cartesianas que acabamos de describir, donde los\(y\) ejes\(x\) y son perpendiculares y comparten un origen común, como se muestra en la Figura A1.1.2. Cuando corresponda, por convención, solemos elegir el\(y\) eje para que corresponda a la dirección vertical.

Otra opción común es un sistema de coordenadas “polares”, donde la posición de un objeto se especifica por una distancia al origen\(r\), y un ángulo,\(\theta\), relativo a una dirección especificada, como se muestra en la Figura A1.1.4. A menudo, un sistema de coordenadas polares se define junto a un sistema cartesiano, de manera que esa\(r\) es la distancia al origen del sistema cartesiano y\(\theta\) es el ángulo con respecto al\(x\) eje.

Figura A1.1.4: Ejemplo de un sistema de coordenadas polares y un punto\(P\) con coordenadas\((r, θ)\).

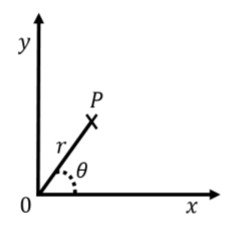
Uno puede convertir fácilmente entre las dos coordenadas cartesianas,\(x\) y\(y\), y las dos coordenadas polares correspondientes,\(r\) y\(\theta\): Las coordenadas\[\begin{aligned} x&=r\cos(\theta)\\ y&=r\sin(\theta)\\ r&=\sqrt{x^2+y^2}\\ \tan(\theta) &= \frac{y}{x}\end{aligned}\] polares se utilizan a menudo para describir el movimiento de un objeto que se mueve alrededor de un círculo, ya que esto significa que solo una de las coordenadas (\(\theta\)) cambia con el tiempo (si se elige el origen del sistema de coordenadas para que coincida con el centro del círculo).

Sistemas de coordenadas 3D

En tres dimensiones, necesitamos especificar tres números para describir la posición de un objeto (por ejemplo, un pájaro volando en el aire). En un sistema de coordenadas cartesianas tridimensionales, simplemente agregamos un tercer eje\(z\),, que es mutuamente perpendicular a ambos\(x\) y\(y\). La posición de un objeto se puede especificar mediante el uso de las tres coordenadas,\(x\),\(y\), y\(z\). Por convención, utilizamos el\(z\) eje para ser la dirección vertical en tres dimensiones.

Dos sistemas de coordenadas adicionales son comunes en tres dimensiones: coordenadas “cilíndricas” y “esféricas”. Los tres sistemas se ilustran en la Figura A1.1.5 superpuestos sobre el sistema cartesiano.

Figura A1.1.5: Sistemas de coordenadas cartesianos (izquierda), cilíndricos (centro) y esféricos (derecha) utilizados en tres dimensiones. Los\(z\) ejes\(y\) y están en el plano de la página, mientras que el\(x\) eje sale de la página.

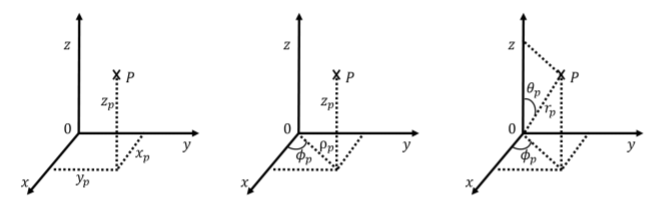
Las coordenadas cilíndricas pueden considerarse como una extensión de las coordenadas polares. Mantenemos la misma coordenada cartesiana\(z\) para indicar la altura por encima del\(xy\) plano, sin embargo, utilizamos el ángulo azimutal\(\phi\), y el radio\(\rho\),, para describir la posición de la proyección de un punto sobre el \(xy\)avión. \(\phi\)es el ángulo entre el\(x\) eje y la línea desde el origen hasta la proyección del punto en el\(xy\) plano y\(\rho\) es la distancia entre el punto y el\(z\) eje. Así, las coordenadas cilíndricas son muy similares al sistema de coordenadas polares introducido en dos dimensiones, excepto con la adición de la\(z\) coordenada. Las coordenadas cilíndricas son útiles para describir situaciones con simetría acimutal, como el movimiento a lo largo de la superficie de un cilindro. Por ejemplo, considere punto\(P\) en la Figura A1.1.6. El punto\(P\) se ubica a una\(\rho\) distancia del\(z\) eje, ya que se ubica en la superficie del cilindro (el extremo circular del cilindro tiene un radio\(\rho\)). Punto\(P\) es una altura\(z\) por encima del\(xy\) plano, y una línea del\(z\) eje al punto\(P\) forma un ángulo\(\phi\) con el\(x\) eje.

Figura A1.1.6: Describiendo la posición de\(P\), ubicada en la superficie de un cilindro, en coordenadas cilíndricas.

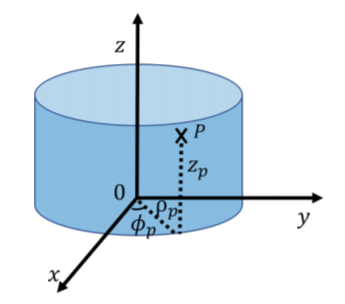
Las coordenadas cilíndricas están relacionadas con las coordenadas cartesianas por:\[\begin{aligned} \rho &= \sqrt{x^2+y^2}\\ \tan(\phi) &= \frac{y}{x}\\ z&=z\end{aligned}\] En coordenadas esféricas, un punto\(P\) se describe por el radio\(r\), el ángulo\(\theta\) polar y el ángulo azimutal, \(\phi\). El radio es la distancia entre el punto y el origen. El ángulo polar es el ángulo con el\(z\) eje que es hecho por la línea desde el origen hasta el punto. El ángulo azimutal se define de la misma manera que en las coordenadas polares. Tenga en cuenta que el valor de\(\phi\) debe estar entre\(0\) y\(2\pi\), mientras que el valor de\(\theta\) debe estar entre\(0\) y\(\pi\).

Las coordenadas esféricas son útiles para describir situaciones que tienen simetría esférica, como una persona que camina sobre la superficie de la Tierra, ya que la coordenada radial no cambiará. Por ejemplo, esto se muestra con Punto\(P\) en la Figura A1.1.7, ubicado en la superficie de una esfera de radio\(r\).

Figura A1.1.7: Describiendo la posición de\(P\), ubicada en la superficie de una esfera, en coordenadas esféricas.

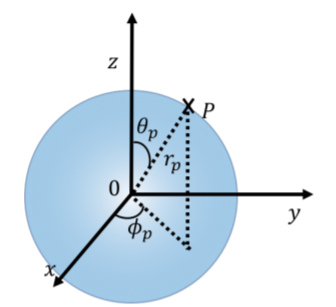
Las coordenadas esféricas están relacionadas con las coordenadas cartesianas por:\[\begin{aligned} r &= \sqrt{x^2+y^2+z^2}\\ \cos(\theta) &= \frac{z}{r}=\frac{z}{\sqrt{x^2+y^2+z^2}}\\ \tan(\phi) &= \frac{y}{x}\\\end{aligned}\]