26.1: Funciones de los números reales

Última actualización
Guardar como PDF

Page ID: 129544

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En el cálculo, trabajamos con funciones y sus propiedades, más que con variables como lo hacemos en álgebra. Generalmente nos preocupa describir funciones en términos de su pendiente, el área (o volúmenes) que encierran, su curvatura, sus raíces (cuando tienen un valor de cero) y su continuidad. Las funciones que examinaremos son un mapeo de uno o más números reales independientes a un número real. Por convención, utilizaremos\(x,y,z\) para indicar variables independientes, y\(f()\) y\(g()\), para denotar funciones. Por ejemplo, si decimos:\[\begin{aligned} f(x) &= x^2\\ \therefore f(2) &= 4\end{aligned}\] queremos decir que\(f(x)\) es una función que se puede evaluar para cualquier número real,\(x\), y el resultado de evaluar la función es cuadrar el número\(x\). En la segunda línea, evaluamos la función con\(x=2\). Del mismo modo, podemos tener una función,\(g(x,y)\) de múltiples variables:\[\begin{aligned} g(x,y)&=x^2+2y^2\\ \therefore g(2,3)&=22\end{aligned}\]

Podemos visualizar fácilmente una función de 1 variable trazándola, como en la Figura A2.1.1.

Figura A2.1.1:\(f(x)=x^{2}\) trazado entre\(x=-5\) y\(x=+5\).

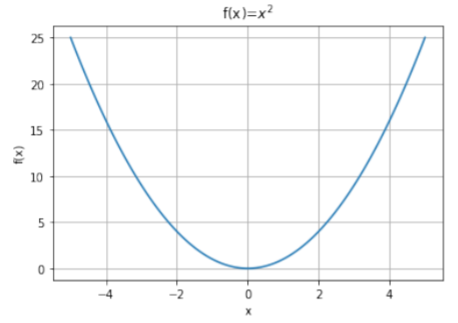
Trazar una función de 2 variables es un poco más complicado, ya que necesitamos hacerlo en tres dimensiones (un eje para\(x\), un eje para\(y\), y un eje para\(g(x,y)\)). La Figura A2.1.2 muestra un ejemplo de graficar una función de 2 variables.

Figura A2.1.2:\(g(x, y) = x^{2} + 2y^{2}\) trazado para\(x\) entre\(-5\) y\(+5\) y para\(y\) entre\(-5\) y\(+5\). Una función de dos variables se puede visualizar como una superficie en tres dimensiones. También se puede visualizar la función observando sus “contornos” (las líneas dibujadas en el\(xy\) plano).

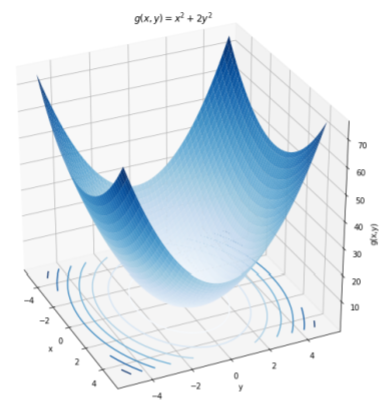
Desafortunadamente, se hace difícil visualizar funciones de más de 2 variables, aunque normalmente se pueden observar proyecciones de esas funciones para intentar visualizar algunas de las características (por ejemplo, los mapas de contorno son proyecciones 2D de superficies 3D, como se muestra en el\(xy\) plano de la Figura A1.1.2). Cuando te encuentras con una función, es una buena práctica intentar visualizarla si puedes. Por ejemplo, hágase las siguientes preguntas:

¿La función tiene uno o más máximos y/o mínimos?
¿La función cruza cero?
¿La función es continua en todas partes?
¿La función siempre se define para algún valor de las variables independientes?