26.2: Derivados

Considera la función\(f(x)=x^2\) que se traza en la Figura A2.1.1. Para cualquier valor de\(x\), podemos definir la pendiente de la función como la “pendiente de la curva”. Para los valores de\(x>0\) la función aumenta a medida que\(x\) aumenta, por lo que decimos que la pendiente es positiva. Para los valores de\(x<0\), la función disminuye a medida que\(x\) aumenta, por lo que decimos que la pendiente es negativa. Un sinónimo de la palabra pendiente es “derivado”, que es la palabra que preferimos usar en el cálculo. A la derivada de una función\(f(x)\) se le da el símbolo\(\frac{df}{dx}\) para indicar que nos estamos refiriendo a la pendiente de\(f(x)\) cuando se grafica como una función de\(x\).

Necesitamos especificar qué variable estamos tomando la derivada con respecto a cuando la función tiene más de una variable pero solo una de ellas debe considerarse independiente. Por ejemplo, la función\(f(x)=ax^2+b\) tendrá diferentes valores si\(a\) y\(b\) se cambian, por lo que tenemos que ser precisos al especificar que estamos tomando la derivada con respecto a\(x\). Las siguientes notaciones son formas equivalentes de decir que estamos tomando la derivada de\(f(x)\) con respecto a\(x\):\[\begin{aligned} \frac{df}{dx}=\frac{d}{dx} f(x) = f'(x) = f'\end{aligned}\] La notación con el prime (\(f'(x),f'\)) puede ser útil para indicar que la derivada en sí misma también es una función de\(x\).

La pendiente (derivada) de una función nos indica qué tan rápido cambia el valor de la función cuando la variable independiente está cambiando. Porque\(f(x)=x^2\), a medida que\(x\) se vuelve más y más positiva, la función se vuelve cada vez más pronunciada; la derivada está aumentando así con\(x\). El signo de la derivada nos indica si la función está aumentando o disminuyendo, mientras que su valor absoluto indica qué tan rápido está cambiando la función (qué tan empinada es).

Podemos aproximar la derivada evaluando cuánto\(f(x)\) cambia cuando\(x\) cambia en una pequeña cantidad, digamos,\(\Delta x\). En el límite de\(\Delta x\to 0\), obtenemos el derivado. De hecho, esta es la definición formal del derivado:

\[\frac{df}{dx}=\lim_{\Delta x\to 0}\frac{\Delta f}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\]

donde\(\Delta f\) esta el pequeno cambio en\(f(x)\) que corresponde al pequeno cambio,\(\Delta x\), en\(x\). Esto hace más clara la notación para la derivada,\(dx\) está\(\Delta x\) en el límite donde\(\Delta x\to0\), y\(df\) está\(\Delta f\), en el mismo límite de\(\Delta x\to 0\).

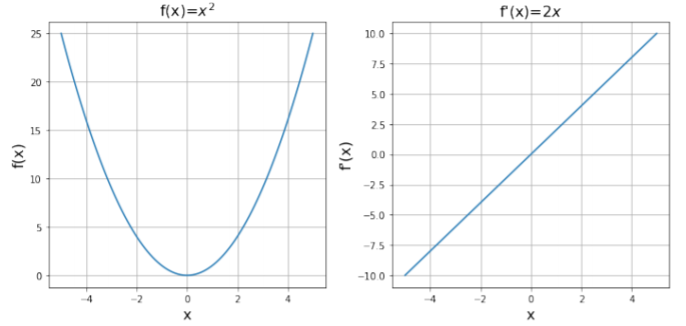
A modo de ejemplo, determinemos la función\(f'(x)\) que es la derivada de\(f(x)=x^2\). Empezamos calculando\(\Delta f\): Ahora\[\begin{aligned} \Delta f &= f(x+\Delta x)-f(x)\\ &=(x+\Delta x)^2 - x^2\\ &=x^2+2x\Delta x+\Delta x^2 -x^2\\ &=2x\Delta x+\Delta x^2\end{aligned}\] calculamos\(\frac{\Delta f}{\Delta x}\):\[\begin{aligned} \frac{\Delta f}{\Delta x}&=\frac{2x\Delta x+\Delta x^2}{\Delta x}\\ &=2x+\Delta x\end{aligned}\] y tomamos el límite\(\Delta x\to 0\): Así\[\begin{aligned} \frac{df}{dx}&=\lim_{\Delta x\to 0 }\frac{\Delta f}{\Delta x}\\ &=\lim_{\Delta x\to 0 }(2x+\Delta x)\\ &=2x\end{aligned}\] hemos encontrado que la función,\(f'(x)=2x\), es la derivada de la función\(f(x)=x^2\). Esto se ilustra en la Figura A2.2.1. Tenga en cuenta que:

• Porque\(x>0\),\(f'(x)\) es positivo y va aumentando con el aumento\(x\), tal y como describimos anteriormente (la función\(f(x)\) es cada vez mayor y cada vez más pronunciada).
• Porque\(x<0\),\(f'(x)\) es negativo y decreciente en magnitud a medida que\(x\) aumenta. Así\(f(x)\) disminuye y se vuelve menos empinada a medida que\(x\) aumenta.
• At\(x=0\),\(f'(x)=0\) indicando que, en el origen, la función\(f(x)\) es (momentáneamente) plana.

Figura A2.2.1:\(f(x)=x^{2}\) y su derivada,\(d'(x)=2x\) trazada para\(x\) entre\(-5\) y\(+5\).

Ejercicio\(\PageIndex{1}\)

Cuando una función tiene un máximo, su derivada en ese punto

1. también tiene un máximo
2. es cero
3. tiene un mínimo
4. es infinito

Contestar

Derivados y propiedades comunes

Está fuera del alcance de este documento derivar la forma funcional de la derivada para cualquier función usando la Ecuación A2.2.1. El cuadro A2.2.1 a continuación da las derivadas para las funciones comunes. En todos los casos,\(x\) es la variable independiente, y todas las demás variables deben considerarse como constantes:

Función,\(f(x)\)	Derivada,\(f'(x)\)
\ (f (x)\) ">\(f(x)=a\)	\ (f' (x)\) ">\(f'(x)=0\)
\ (f (x)\) ">\(f(x)=x^n\)	\ (f' (x)\) ">\(f'(x)=nx^{n-1}\)
\ (f (x)\) ">\(f(x)=\sin(x)\)	\ (f' (x)\) ">\(f'(x)=\cos(x)\)
\ (f (x)\) ">\(f(x)=\cos(x)\)	\ (f' (x)\) ">\(f'(x)=-\sin(x)\)
\ (f (x)\) ">\(f(x)=\tan(x)\)	\ (f' (x)\) ">\(f'(x)=\frac{1}{\cos^2(x)}\)
\ (f (x)\) ">\(f(x)=e^x\)	\ (f' (x)\) ">\(f'(x)=e^x\)
\ (f (x)\) ">\(f(x)=\ln(x)\)	\ (f' (x)\) ">\(f'(x)=\frac{1}{x}\)

Cuadro A2.2.1: Derivadas comunes de funciones.

Si dos funciones de 1 variable,\(f(x)\) y\(g(x)\), se combinan en una tercera función\(h(x)\),, entonces hay reglas simples para encontrar la derivada,\(h'(x)\), basadas en las derivadas\(f'(x)\) y\(g'(x)\). Estos se resumen en la Tabla A2.2.2 a continuación.

Función,\(h(x)\)	Derivada,\(h'(x)\)
\ (h (x)\) ">\(h(x)=f(x)+g(x)\)	\ (h' (x)\) ">\(h'(x)=f'(x)+g'(x)\)
\ (h (x)\) ">\(h(x)=f(x)-g(x)\)	\ (h' (x)\) ">\(h'(x)=f'(x)-g'(x)\)
\ (h (x)\) ">\(h(x)=f(x)g(x)\)	\ (h' (x)\) ">\(h'(x)=f'(x)g(x)+f(x)g'(x)\) (La regla del producto)
\ (h (x)\) ">\(h(x)=\frac{f(x)}{g(x)}\)	\ (h' (x)\) ">\(h'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\) (La regla del cociente)
\ (h (x)\) ">\(h(x)=f(g(x))\)	\ (h' (x)\) ">\(h'(x)=f'(g(x))g'(x)\) (La regla de la cadena)

Cuadro A2.2.2: Derivadas de funciones combinadas.

Ejemplo\(\PageIndex{1}\)

Utilice las propiedades de la Tabla A2.2.2 para mostrar que la derivada\(\tan(x)\) de\(\frac{1}{\cos^2(x)}\).

Solución:

Ya que\(\tan(x)=\frac{\sin(x)}{\cos(x)}\), podemos escribir:\[\begin{aligned} h(x) &= \frac{f(x)}{g(x)} \\ f(x) &= \sin(x)\\ g(x) &= \cos(x)\end{aligned}\] Usando la cuarta fila en la Tabla A2.2.2, y las derivadas comunes de la Tabla A2.2.1, tenemos:\[\begin{aligned} f'(x) &= \cos(x) \\ g'(x) &= -\sin(x) \\ g^2(x) &= \cos^2(x) \\ h'(x) &=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\\ &= \frac{\cos(x)\cos(x) - \sin(x) (-\sin(x))}{\cos^2}\\ &=\frac{\cos^2(x)+\sin^2(x)}{\cos^2}\\ &=\frac{1}{\cos^2(x)}\end{aligned}\] según se requiera.

Ejemplo\(\PageIndex{2}\)

Utilice las propiedades de la Tabla A2.2.2 para calcular la derivada de\(h(x)=\sin^2(x)\).

Solución:

Para calcular la derivada de\(h(x)\), necesitamos usar la Regla de Cadena. \(h(x)\)se encuentra tomando primero\(\sin(x)\) y luego tomando ese resultado al cuadrado. Podemos así identificar:\[\begin{aligned} h(x) &= \sin^2(x) = f(g(x))\\ f(x) &= x^2 \\ g(x) &= \sin(x)\end{aligned}\] Usando las derivadas comunes de la Tabla A2.2.1, tenemos:\[\begin{aligned} f'(x) &= 2x \\ g'(x) &= \cos(x)\end{aligned}\] Aplicando la Regla de Cadena, tenemos:\[\begin{aligned} h'(x) &= f'(g(x))g'(x)\\ &= 2\sin(x)g'(x)\\ &= 2\sin(x)\cos(x)\end{aligned}\] donde las\(f'(g(x))\) medias aplican la derivada de\(f(x)\) a la función\(g(x)\). Ya que la derivada de\(f(x)\) es\(f'(x)=2x\), cuando la aplicamos a\(g(x)\) en lugar de\(2x\), obtenemos\(2g(x)=2\cos(x)\).

Derivadas parciales y gradientes

Hasta el momento, solo hemos mirado la derivada de una función de una sola variable independiente y la hemos usado para cuantificar cuánto cambia la función cuando cambia la variable independiente. Podemos proceder análogamente para una función de múltiples variables\(f(x,y)\), cuantificando cuánto cambia la función a lo largo de la dirección asociada a una variable particular. Esto se ilustra en la Figura A2.2.2 para la función\(f(x,y)=x^2-2y^2\), que se parece un poco a un sillín.

Figura A2.2.2:\(f(x, y) = x^{2} − 2y^{2}\) trazado para\(x\) entre\(-5\) y\(+5\) y para\(y\) entre\(-5\) y\(+5\). El punto\(P\) etiquetado en la figura muestra el valor de la función at\(f(−2, −2)\). Las dos líneas muestran la función evaluada cuando una de\(x\) o\(y\) se mantiene constante.

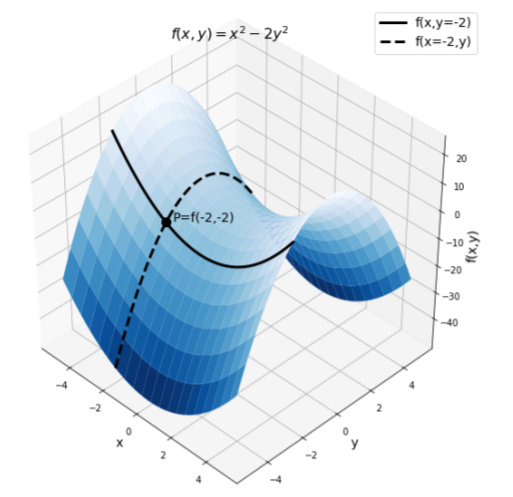
Supongamos que deseamos determinar la derivada de la función\(f(x)\) at\(x=-2\) y\(y=-2\). En este caso, no tiene sentido simplemente determinar el “derivado”, sino más bien, debemos especificar en qué dirección queremos la derivada. Es decir, necesitamos especificar en qué dirección nos interesa cuantificar la tasa de cambio de la función.

Una posibilidad es cuantificar la tasa de cambio en la\(x\) dirección. La línea continua en la Figura A2.2.2 muestra la parte de la superficie de función donde\(y\) se fija en -2, es decir, la función evaluada como\(f(x,y=-2)\). El punto\(P\) de la figura muestra el valor de la función cuando\(x=-2\) y\(y=-2\). Al mirar la línea continua en el punto\(P\), podemos ver que a medida que\(x\) aumenta, el valor de la función disminuye suavemente. La derivada de\(f(x,y)\) con respecto a\(x\) cuándo se mantiene constante y\(y\) se evalúa en\(x=-2\) y, por lo tanto,\(y=-2\) es negativa. Más que decir “La derivada de\(f(x,y)\) con respecto a\(x\) cuándo\(y\) se mantiene constante” decimos “La derivada parcial de\(f(x,y)\) con respecto a\(x\)”.

Dado que la derivada parcial es diferente a la derivada ordinaria (ya que implica que estamos manteniendo fijas variables independientes), le damos un símbolo diferente, es decir, usamos\(\partial\) en lugar de\(d\):

\[\begin{aligned}\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)\quad\text{(Partial derivative of f with respect to x)}\end{aligned}\]

Calcular la derivada parcial es muy fácil, ya que simplemente tratamos todas las variables como constantes excepto la variable con respecto a la que estamos diferenciando ¹. Para la función\(f(x,y)=x^2-2y^2\), tenemos:

\[\begin{aligned} \frac{\partial f}{\partial x}&=\frac{\partial}{\partial x}(x^2-2y^2) = 2x\\ \frac{\partial f}{\partial y}&=\frac{\partial}{\partial y}(x^2-2y^2) = -4y\end{aligned}\]

At\(x=-2\), la derivada parcial de\(f(x,y)\) es efectivamente negativa, consistente con nuestra observación de que, a lo largo de la línea sólida, en el punto\(P\), la función está disminuyendo.

Una función tendrá tantas derivadas parciales como variables independientes. También tenga en cuenta que, al igual que una derivada normal, una derivada parcial sigue siendo una función. La derivada parcial con respecto a una variable nos dice cuán empinada es la función en la dirección en la que esa variable aumenta y si está aumentando o disminuyendo.

Ejemplo\(\PageIndex{3}\)

Determinar las derivadas parciales de\(f(x,y,z)=ax^2+byz-\sin(z)\).

Solución:

En este caso, tenemos tres derivadas parciales para evaluar. Tenga en cuenta que\(a\) son\(b\) constantes y pueden pensarse como números que desconocemos.

\[\begin{aligned} \frac{\partial f}{\partial x}&=\frac{\partial}{\partial x}(ax^2+byz-\sin(z)) = 2ax\\ \frac{\partial f}{\partial y}&=\frac{\partial}{\partial y}(ax^2+byz-\sin(z)) = bz \\ \frac{\partial f}{\partial z}&=\frac{\partial}{\partial z}(ax^2+byz-\sin(z)) = by-\cos(z) \end{aligned}\]

Dado que las derivadas parciales nos dicen cómo cambia la función en una dirección particular, podemos utilizarlas para encontrar la dirección en la que la función cambia más rápidamente. Por ejemplo, supongamos que la superficie de la Figura A2.2.2 corresponde a una superficie física real y que colocamos una bola en punto\(P\). Deseamos saber en qué dirección rodará la pelota. La dirección en la que rodará es la opuesta a la dirección donde\(f(x,y)\) aumenta más rápidamente (es decir, rodará en la dirección donde\(f(x,y)\) disminuye más rápidamente). La dirección en la que la función aumenta más rápidamente se llama el “gradiente” y se denota por\(\nabla f(x,y)\).

Dado que el gradiente es una dirección, no puede ser representado por un solo número. Más bien, usamos un “vector” para indicar esta dirección. Dado que\(f(x,y)\) tiene dos variables independientes, el gradiente será un vector con dos componentes. Los componentes del gradiente vienen dados por las derivadas parciales:\[\begin{aligned} \nabla f(x,y) = \frac{\partial f}{\partial x}\hat x+\frac{\partial f}{\partial y} \hat y\end{aligned}\] donde\(\hat x\) y\(\hat y\) son los vectores unitarios en las\(y\) direcciones\(x\) y, respectivamente (a veces, los vectores unitarios se denotan\(\hat i\) y\(\hat j\)). La dirección del gradiente nos indica en qué dirección aumenta la función más rápido, y la magnitud del gradiente nos indica cuánto aumenta la función en esa dirección.

Ejemplo\(\PageIndex{4}\)

Determinar el gradiente de la función\(f(x,y)=x^2-2y^2\) at the point \(x=-2\) and \(y=-2\).

Solución:

Ya hemos encontrado las derivadas parciales que necesitamos evaluar en\(x=-2\) y\(y=-2\):\[\begin{aligned} \frac{\partial f}{\partial x}&= 2x\\ \frac{\partial f}{\partial y}&= -4y \\ \therefore \nabla f(x,y) &= \frac{\partial f}{\partial x}\hat x+\frac{\partial f}{\partial y} \hat y \\ &=2x\hat x-4y\hat y\end{aligned}\] Evaluando el gradiente en\(x=-2\) y\(y=-2\):\[\begin{aligned} \nabla f(x,y) &= 2x\hat x-4y\hat y\\ &=-4 \hat x + 8 \hat y\\ &=4 (-\hat x+2\hat y)\\\end{aligned}\] El vector de gradiente apunta en la dirección\((-1,2)\). Es decir, la función aumenta más en la dirección donde tomarías 1 ritmo en la\(x\) dirección negativa y 2 pasos en la\(y\) dirección positiva. Puedes confirmarlo mirando el punto\(P\) de la Figura A2.2.2 e imaginando en qué dirección tendrías que ir para subir la superficie para obtener la subida más empinada.

El gradiente es en sí mismo una función, pero no es una función real (en el sentido de un número real), ya que evalúa a un vector. Se trata de un mapeo de números reales\(x,y\) a un vector. A medida que tomes cursos de cálculo más avanzados, eventualmente te encontrarás con “cálculo vectorial”, que es solo el cálculo para funciones de múltiples variables a las que te acaban de presentar. El punto clave a recordar aquí es que el gradiente se puede utilizar para encontrar el vector que apunta en la dirección del aumento máximo de la función multivariada correspondiente. Esta es precisamente la cantidad que necesitamos en física para determinar en qué dirección rodará una bola cuando se coloque sobre una superficie (rodará en la dirección opuesta al vector de gradiente).

Ejercicio\(\PageIndex{2}\)

El gradiente de una función de una variable,\(f(x)\), is

1. undefined
2. cero
3. igual a su derivada
4. infinito

Contestar

Usos comunes de los derivados en la física

El caso más sencillo de usar una derivada es describir la velocidad de un objeto. Si un objeto cubre una distancia\(\Delta x\) en un periodo de tiempo\(\Delta t\), es “velocidad promedio”\(v_{avg}\), se define como la distancia recorrida por el objeto dividida por la cantidad de tiempo que tardó en cubrir esa distancia:\[\begin{aligned} v_{avg} = \frac{\Delta x}{\Delta t}\end{aligned}\] Si el objeto cambia de velocidad (por ejemplo se está desacelerando) sobre la distancia\(\Delta x\), todavía podemos definir su “velocidad instantánea”\(v\),, midiendo la cantidad de tiempo\(\Delta t\),, que lleva al objeto cubrir una distancia muy pequeña,\(\Delta x\). La velocidad instantánea se define en el límite donde\(\Delta x \to 0\):\[\begin{aligned} v = \lim_{\Delta x\to 0}\frac{\Delta x}{\Delta t}=\frac{dx}{dt}\end{aligned}\] que es precisamente la derivada de\(x(t)\) con respecto a\(t\). \(x(t)\)es una función que da la posición,\(x\), del objeto a lo largo de algún\(x\) eje en función del tiempo. La velocidad del objeto es así la velocidad de cambio de su posición.

De igual manera, si la velocidad va cambiando con el tiempo, entonces podemos definir la “aceleración”\(a\), de un objeto como la velocidad de cambio de su velocidad:\[\begin{aligned} a = \frac{dv}{dt}\end{aligned}\]

Notas al pie

1. ¡Tomar la derivada es “diferenciar”!