26.3: Antiderivados e integrales

En el apartado anterior, nos preocupaba determinar la derivada de una función\(f(x)\). La derivada es útil porque nos dice cómo\(f(x)\) varía la función en función de\(x\). En física, a menudo sabemos cómo varía una función, pero no conocemos la función real. En otras palabras, a menudo tenemos el problema opuesto: se nos da la derivada de una función, y deseamos determinar la función real. Para este caso, limitaremos nuestra discusión a funciones de una sola variable independiente.

Supongamos que se nos da una función\(f(x)\) y sabemos que ésta es la derivada de alguna otra función\(F(x)\),, que desconocemos. Llamamos\(F(x)\) al anti-derivado de\(f(x)\). El anti-derivado de una función\(f(x)\), escrito\(F(x)\), satisface así la propiedad:\[\begin{aligned} \frac{dF}{dx}=f(x)\end{aligned}\] Como tenemos un símbolo para indicar que tomamos la derivada con respecto a\(x\) (\(\frac{d}{dx}\)), también tenemos un símbolo, \(\int dx\), por indicar que tomamos el antiderivado con respecto a\(x\):\[\begin{aligned} \int f(x) dx &= F(x) \\ \therefore \frac{d}{dx}\left(\int f(x) dx\right) &= \frac{dF}{dx}=f(x)\end{aligned}\] Anteriormente, justificamos el símbolo para la derivada señalando que es como\(\frac{\Delta f}{\Delta x}\) pero para el caso cuando\(\Delta x\to 0\). De igual manera, justificaremos el signo antiderivado\(\int f(x) dx\),, al demostrar que está relacionado con una suma de\(f(x)\Delta x\), en el límite\(\Delta x\to 0\). El\(\int\) letrero parece una “S” por suma.

Si bien es posible determinar exactamente la derivada de una función\(f(x)\), la anti-derivada solo se puede determinar hasta una constante. Consideremos por ejemplo una función diferente,\(\tilde F(x)=F(x)+C\), donde\(C\) es una constante. La derivada de\(\tilde F(x)\) con respecto a\(x\) viene dada por:\[\begin{aligned} \frac{d\tilde{F}}{dx}&=\frac{d}{dx}\left(F(x)+C\right)\\ &=\frac{dF}{dx}+\frac{dC}{dx}\\ &=\frac{dF}{dx}+0\\ &=f(x)\end{aligned}\] Por lo tanto, la función\(\tilde F(x)=F(x)+C\) es también un anti-derivado de\(f(x)\). La constante a menudo se\(C\) puede determinar usando información adicional (a veces llamada “condiciones iniciales”). Recordemos la función,\(f(x)=x^2\), mostrada en la Figura A2.2.1 (panel izquierdo). Si imaginas cambiar toda la función hacia arriba o hacia abajo, la derivada no cambiaría. Es decir, si el origen de los ejes no estuviera dibujado en el panel izquierdo, seguirías siendo capaz de determinar la derivada de la función (qué tan empinada es). Agregar una constante,\(C\), a una función es exactamente lo mismo que desplazar la función hacia arriba o hacia abajo, lo que no cambia su derivada. Así, cuando conoces la derivada, no puedes conocer el valor de\(C\), a menos que también te digan que la función debe pasar por un punto específico (una llamada condición inicial).

Para determinar la derivada de una función, se utilizó la Ecuación A2.2.1. Ahora necesitamos derivar una prescripción equivalente para determinar el antiderivado. Supongamos que tenemos los dos datos requeridos para determinar\(F(x)\) completamente, a saber:

1. la función\(f(x)=\frac{dF}{dx}\) (su derivada).
2. la condición que\(F(x)\) debe pasar por un punto específico,\(F(x_0)=F_0\).

Figura A2.3.1: Determinar la anti-derivada\(F(x)\), dada la función\(f(x) = 2x\) y la condición inicial que\(F(x)\) pasa por el punto\((x_{0}, F_{0}) = (1, 3)\).

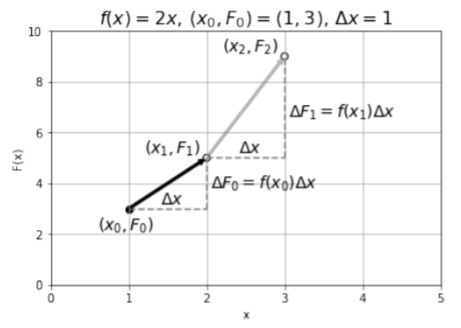
El procedimiento para determinar el antiderivado\(F(x)\) se ilustra anteriormente en la Figura A2.3.1. Empezamos dibujando el punto por el que sabemos que\(F(x)\) debe pasar la función,\((x_0,F_0)\). Luego elegimos un valor de\(\Delta x\) y usamos la derivada,\(f(x)\), para calcular\(\Delta F_0\), la cantidad por la cual\(F(x)\) cambia cuando\(x\) cambia por\(\Delta x\). Usando la derivada\(f(x)\) evaluada en\(x_0\), tenemos:\[\begin{aligned} \frac{\Delta F_0}{\Delta x} &\approx f(x_0)\;\;\;\; (\text{in the limit} \Delta x\to 0 )\\ \therefore \Delta F_0 &= f(x_0) \Delta x\end{aligned}\] Podemos entonces estimar el valor de la función\(F_1=F(x_1)\) en el siguiente punto,\(x_1=x_0+\Delta x\), como lo ilustra la flecha negra en la Figura A2.3.1\[\begin{aligned} F_1&=F(x_1)\\ &=F(x+\Delta x) \\ &\approx F_0 + \Delta F_0\\ &\approx F_0+f(x_0)\Delta x\end{aligned}\] Ahora que tenemos determinó el valor de la función\(F(x)\) en\(x=x_1\), podemos repetir el procedimiento para determinar el valor de la función\(F(x)\) en el siguiente punto,\(x_2=x_1+\Delta x\). Nuevamente, usamos la derivada evaluada en\(x_1\)\(f(x_1)\),, para determinar\(\Delta F_1\), y agregamos eso\(F_1\) para obtener\(F_2=F(x_2)\), como lo ilustra la flecha gris en la Figura A2.3.1:\[\begin{aligned} F_2&=F(x_1+\Delta x) \\ &\approx F_1+\Delta F_1\\ &\approx F_1+f(x_1)\Delta x\\ &\approx F_0+f(x_0)\Delta x+f(x_1)\Delta x\end{aligned}\] Usando la notación de suma, podemos generalizar el resultado y escribir la función\(F(x)\) evaluada en cualquier punto,\(x_N=x_0+N\Delta x\):\[\begin{aligned} F(x_N) \approx F_0+\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x\end{aligned}\] El resultado anterior será exactamente correcto en el límite\(\Delta x\to 0\):

\[F(x_N) = F(x_0)+\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x\]

Echemos un vistazo más de cerca a la suma. Cada término en la suma es de la forma\(f(x_{i-1})\Delta x\), y se ilustra en la Figura A2.3.2 para el mismo caso que en la Figura A2.3.1 (es decir, la Figura A2.3.2 muestra\(f(x)\) que sabemos, y la Figura A2.3.1 muestra\(F(x)\) que estamos tratando de encontrar).

Figura A2.3.2: La función\(f(x) = 2x\) e ilustración de los términos\(f(x_{0})∆x\) y\(f(x_{1})∆x\) como el área entre la curva\(f(x)\) y el\(x\) eje cuando\(∆x → 0\).

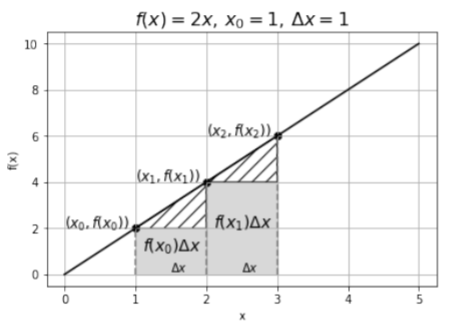
Como puedes ver, cada término en la suma corresponde al área de un rectángulo entre la función\(f(x)\) y el\(x\) eje (con una pieza faltante). En el límite donde\(\Delta x\to 0\), las piezas faltantes (mostradas por las áreas hash en la Figura A2.3.2)\(f(x_i)\Delta x\) desaparecerán y se convertirán exactamente en el área entre\(f(x)\) y el\(x\) eje sobre una longitud\(\Delta x\). La suma de las áreas rectangulares se acercará así al área entre\(f(x)\) y el\(x\) eje entre\(x_0\) y\(x_N\):\[\begin{aligned} \lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x=\text{Area between f(x) and x axis from $x_0$ to $x_N$}\end{aligned}\]

Reorganizar la Ecuación A2.3.1 nos da una receta para determinar el anti-derivado:\[\begin{aligned} F(x_N) - F(x_0)&=\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x\end{aligned}\] Vemos que si determinamos el área entre\(f(x)\) y el\(x\) eje de\(x_0\) a\(x_N\), podemos obtener la diferencia entre el anti-derivado en dos puntos,\(F(x_N)-F(x_0)\)

La diferencia entre el anti-derivado,\(F(x)\), evaluado a dos valores diferentes de\(x\) se llama la integral de\(f(x)\) y tiene la siguiente notación:

\[\int_{x_0}^{x_N}f(x) dx=F(x_N) - F(x_0)=\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x\]

Como puede ver, la integral tiene etiquetas que especifican el rango sobre el cual calculamos el área entre\(f(x)\) y el\(x\) eje. Una notación común para expresar la diferencia\(F(x_N) - F(x_0)\) es usar corchetes:\[\begin{aligned} \int_{x_0}^{x_N}f(x) dx=F(x_N) - F(x_0) =\big [ F(x) \big]_{x_0}^{x_N}\end{aligned}\]

Recordemos que antes escribimos el anti-derivado con el mismo\(\int\) símbolo:\[\begin{aligned} \int f(x) dx = F(x)\end{aligned}\] El símbolo\(\int f(x) dx\) sin los límites se llama la integral indefinida. También puedes ver que cuando tomas la integral (definitiva) (es decir, la diferencia entre\(F(x)\) evaluada en dos puntos), cualquier constante a la que se agregue\(F(x)\) se cancelará. Las cantidades físicas siempre se basan en integrales definidas, por lo que cuando escribimos la constante\(C\) es principalmente para la integridad y para enfatizar que tenemos una integral indefinida.

A modo de ejemplo, determinemos la integral de\(f(x)=2x\) entre\(x=1\) y\(x=4\), así como la integral indefinida de\(f(x)\), que es el caso que ilustramos en las figuras A2.3.1 y A2.3.2. Usando la Ecuación A2.3.2, tenemos:\[\begin{aligned} \int_{x_0}^{x_N}f(x) dx&=\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x \\ &=\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} 2x_{i-1} \Delta x \end{aligned}\] donde tenemos:\[\begin{aligned} x_0 &=1 \\ x_N &=4 \\ \Delta x &= \frac{x_N-x_0}{N}\end{aligned}\] Tenga en cuenta que\(N\) es el número de veces que tenemos\(\Delta x\) en el intervalo entre\(x_0\) y\(x_N\). Así, tomar el límite de\(\Delta x\to 0\) es lo mismo que tomar el límite\(N\to\infty\). Ilustremos la suma para el caso donde\(N=3\), y así cuándo\(\Delta x=1\), correspondiente a la ilustración de la Figura A2.3.2:\[\begin{aligned} \sum_{i=1}^{i=N=3} 2x_{i-1} \Delta x &=2x_0\Delta x+2x_1\Delta x+2x_2\Delta x\\ &=2\Delta x (x_0+x_1+x_2) \\ &=2 \frac{x_3-x_0}{N}(x_0+x_1+x_2) \\ &=2 \frac{(4)-(1)}{(3)}(1+2+3) \\ &=12\end{aligned}\] donde en la segunda línea, notamos que podíamos factorizar el\(2\Delta x\) porque aparece en cada término. Como solo usamos 4 puntos, esta es una aproximación bastante gruesa de la integral, y esperamos que sea una subestimación (ya que el área faltante representada por las líneas hash en la Figura A2.3.2 es bastante grande).

Si repetimos esto para un valor mayor de N,\(N=6\) (\(\Delta x = 0.5\)), deberíamos obtener una respuesta más precisa:\[\begin{aligned} \sum_{i=1}^{i=6} 2x_{i-1} \Delta x &=2 \frac{x_6-x_0}{N}(x_0+x_1+x_2+x_3+x_4+x_5)\\ &=2\frac{4-1}{6} (1+1.5+2+2.5+3+3.5)\\ &=13.5\end{aligned}\]

Escribiendo esto nuevamente para el caso general para que podamos tomar el límite\(N\to\infty\), y factorizando el\(2\Delta x\):\[\begin{aligned} \sum_{i=1}^{i=N} 2x_{i-1} \Delta x &=2 \Delta x\sum_{i=1}^{i=N}x_{i-1}\\ &=2 \frac{x_N-x_0}{N}\sum_{i=1}^{i=N}x_{i-1}\end{aligned}\] Ahora, considere la combinación:\[\begin{aligned} \frac{1}{N}\sum_{i=1}^{i=N}x_{i-1}\end{aligned}\] que aparece arriba. Esto corresponde al promedio aritmético de los valores de\(x_0\) a\(x_{N-1}\) (suma los valores y divide por el número de valores). En el límite donde\(N\to \infty\), luego el valor\(x_{N-1}\approx x_N\). El valor promedio de\(x\) en el intervalo entre\(x_0\) y\(x_N\) viene dado simplemente por el valor de\(x\) en el punto medio del intervalo:\[\begin{aligned} \lim_{N\to\infty}\frac{1}{N}\sum_{i=1}^{i=N}x_{i-1}=\frac{1}{2}(x_N+x_0)\end{aligned}\] Poner todo junto:\[\begin{aligned} \lim_{N\to\infty}\sum_{i=1}^{i=N} 2x_{i-1} \Delta x &=2 (x_N+x_0)\lim_{N\to\infty}\frac{1}{N}\sum_{i=1}^{i=N}x_{i-1}\\ &=2 (x_N-x_0)\frac{1}{2}(x_N+x_0)\\ &=x_N^2 - x_0^2\\ &=(4)^2 - (1)^2 = 15\end{aligned}\] donde en la última línea, sustituimos en los valores de\(x_0=1\) y\(x_N=4\). Escribiendo esto como la integral:\[\begin{aligned} \int_{x_0}^{x_N}2x dx=F(x_N) - F(x_0)=x_N^2 - x_0^2\end{aligned}\] podemos identificar inmediatamente la integral antiderivada y la indefinida:\[\begin{aligned} F(x) &= x^2 +C \\ \int 2xdx&=x^2 +C\end{aligned}\] Este es por supuesto el resultado que esperábamos, y podemos verificar nuestra respuesta tomando la derivada de\(F(x)\): Así\[\begin{aligned} \frac{dF}{dx}=\frac{d}{dx}(x^2+C) = 2x\end{aligned}\] hemos confirmado que \(F(x)=x^2+C\)es el anti-derivado de\(f(x)=2x\).

Ejercicio\(\PageIndex{1}\)

La cantidad\(\int_{a}^{b}f(t)dt\) is equal to

1. el área entre la función\(f(t)\) y el\(f\) eje entre\(t=a\) y\(t=b\)
2. la suma de\(f(t)\Delta t\) en el límite\(\Delta t\to 0\) entre\(t=a\) y\(t=b\)
3. la diferencia\(f(b) - f(a)\).

Contestar

Antiderivados comunes y propiedades

El cuadro A2.3.1 a continuación da los antiderivados (integrales indefinidas) para funciones comunes. En todos los casos,\(x,\) es la variable independiente, y todas las demás variables deben considerarse como constantes:

Función,\(f(x)\)	Anti-derivado,\(F(x)\)
\ (f (x)\) ">\(f(x)=a\)	\ (F (x)\) ">\(F(x)=ax+C\)
\ (f (x)\) ">\(f(x)=x^n\)	\ (F (x)\) ">\(F(x)=\frac{1}{n+1}x^{n+1}+C\)
\ (f (x)\) ">\(f(x)=\frac{1}{x}\)	\ (F (x)\) ">\(F(x)=\ln(|x|)+C\)
\ (f (x)\) ">\(f(x)=\sin(x)\)	\ (F (x)\) ">\(F(x)=-\cos(x)+C\)
\ (f (x)\) ">\(f(x)=\cos(x)\)	\ (F (x)\) ">\(F(x)=\sin(x)+C\)
\ (f (x)\) ">\(f(x)=\tan(x)\)	\ (F (x)\) ">\(F(x)=-\ln(|\cos(x)|)+C\)
\ (f (x)\) ">\(f(x)=e^x\)	\ (F (x)\) ">\(F(x)=e^x+C\)
\ (f (x)\) ">\(f(x)=\ln(x)\)	\ (F (x)\) ">\(F(x)=x\ln(x)-x+C\)

Cuadro A2.3.1: Integrales indefinidas comunes de funciones.

Obsérvese que, en general, es mucho más difícil obtener el antiderivado de una función que tomar su derivada. Algunas propiedades comunes para ayudar a evaluar integrales indefinidas se muestran en la Tabla A2.3.2 a continuación.

Anti-derivado	Antiderivado equivalente
\(\int (f(x)+g(x)) dx\)	\(\int f(x)dx+\int g(x) dx\)(suma)
\(\int (f(x)-g(x)) dx\)	\(\int f(x)dx-\int g(x) dx\)(resta)
\(\int af(x) dx\)	\(a\int f(x)dx\)(multiplicación por constante)
\(\int f'(x)g(x) dx\)	\(f(x)g(x)-\int f(x)g'(x) dx\)(integración por partes)

Cuadro A2.3.2: Algunas propiedades de integrales indefinidas.

Usos comunes de las integrales en Física - de una suma a una integral

Las integrales son extremadamente útiles en física porque están relacionadas con sumas. Si asumimos que nuestros amigos matemáticos (o computadoras) pueden determinar antiderivados para nosotros, usar integrales no es tan complicado.

La idea clave en la física es que las integrales son una herramienta para realizar sumas fácilmente. Como vimos anteriormente, las integrales corresponden al área debajo de una curva, la cual se encuentra sumando las (diferentes) áreas de un número infinito de rectángulos infinitamente pequeños. En física, suele darse el caso de que necesitamos tomar la suma de un número infinito de pequeñas cosas que siguen variando, al igual que las áreas de los rectángulos.

Consideremos, por ejemplo, una varilla de longitud\(L\), y masa total\(M\), como se muestra en la Figura A2.3.3. Si la varilla es uniforme en densidad, entonces si la cortamos en, digamos, dos piezas iguales, esas dos piezas pesarán lo mismo. Podemos definir una “densidad de masa lineal”,\(\mu\), para la varilla, como la masa por unidad de longitud de la varilla:\[\begin{aligned} \mu = \frac{M}{L}\end{aligned}\] La densidad de masa lineal tiene dimensiones de masa sobre longitud y puede ser utilizada para encontrar la masa de cualquier longitud de varilla. Por ejemplo, si la varilla tiene una masa de\(M=5\text{kg}\) y una longitud de\(L=2\text{m}\), entonces la densidad de masa es:\[\begin{aligned} \mu=\frac{M}{L}=\frac{(5\text{kg})}{(2\text{m})}=2.5\text{kg/m}\end{aligned}\] Conociendo la densidad de masa, ahora podemos encontrar fácilmente la masa\(m\),, de una pieza de varilla que tiene una longitud de, digamos,\(l=10\text{cm}\). Usando la densidad de masa, la masa de la\(10\text{cm}\) varilla viene dada por:\[\begin{aligned} m=\mu l=(2.5\text{kg/m})(0.1\text{m})=0.25\text{kg}\end{aligned}\] Ahora supongamos que tenemos una varilla de longitud\(L\) que no es uniforme, como en la Figura A2.3.3, y que no tiene una densidad de masa lineal constante. Quizás la varilla se hace cada vez más ancha, o tiene unos agujeros en ella que la hacen no uniforme. Imagínese que la densidad de masa de la varilla viene dada en cambio por una función\(\mu(x)\),, que depende de la posición a lo largo de la varilla, donde\(x\) está la distancia medida desde un lado de la varilla.

Figura A2.3.3: Varilla con una densidad lineal variable. Para calcular la masa de la varilla, consideramos un elemento\(∆m_{i}\) de masa pequeña de longitud\(∆x\) en posición\(x_{i}\). La masa total de la varilla se encuentra sumando la masa de los elementos de masa pequeña.

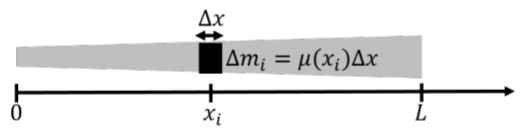
Ahora bien, no podemos simplemente determinar la masa de la varilla multiplicando\(\mu(x)\) y\(L\), ya que no sabemos qué valor de\(x\) usar. De hecho, tenemos que usar todos los valores de\(x\), entre\(x=0\) y\(x=L\).

La estrategia es dividir la varilla en\(N\) trozos de longitud\(\Delta x\). Si etiquetamos nuestras piezas de varilla con un índice\(i\), podemos decir que la pieza que está en posición\(x_i\) tiene una masa diminuta,\(\Delta m_i\). Suponemos que\(\Delta x\) es lo suficientemente pequeño como para que\(\mu(x)\) pueda tomarse como constante sobre la longitud de ese diminuto trozo de varilla. Entonces, el pequeño trozo de varilla en\(x=x_i\), tiene una masa,\(\Delta m_i\), dada por:\[\begin{aligned} \Delta m_i = \mu(x_i) \Delta x\end{aligned}\] donde\(\mu(x_i)\) se evalúa en la posición,\(x_i\), de nuestro pequeño trozo de varilla. La masa total,\(M\), de la varilla es entonces la suma de las masas de las pequeñas varillas, en el límite donde\(\Delta x\to 0\):\[\begin{aligned} M &= \lim_{\Delta x\to 0}\sum_{i=1}^{i=N}\Delta m_i \\ &= \lim_{\Delta x\to 0}\sum_{i=1}^{i=N} \mu(x_i) \Delta x\end{aligned}\] Pero esta es precisamente la definición de la integral (Ecuación A2.3.1), que podemos evaluar fácilmente con un anti-derivado:\[\begin{aligned} M &=\lim_{\Delta x\to 0}\sum_{i=1}^{i=N} \mu(x_i) \Delta x \\ &= \int_0^L \mu(x) dx \\ &= G(L) - G(0)\end{aligned}\] donde\(G(x)\) está el anti-derivado de\(\mu(x)\).

Supongamos que la densidad de masa viene dada por la función:\[\begin{aligned} \mu(x)=ax^3\end{aligned}\] con anti-derivada (Cuadro A2.3.1):\[\begin{aligned} G(x)=a\frac{1}{4}x^4 + C\end{aligned}\] Digamos\(a=5\text{kg/m}^{4}\) y digamos que la longitud de la varilla es\(L=0.5\text{m}\). La masa total de la varilla es entonces:\[\begin{aligned} M&=\int_0^L \mu(x) dx \\ &=\int_0^L ax^3 dx \\ &= G(L)-G(0)\\ &=\left[ a\frac{1}{4}L^4 \right] - \left[ a\frac{1}{4}0^4 \right]\\ &=5\text{kg/m}^{4}\frac{1}{4}(0.5\text{m})^4 \\ &=78\text{g}\\\end{aligned}\]

Con un poco de práctica, puedes resolver este tipo de problemas sin escribir la suma explícitamente. Imagínese una pieza infinitesimal de la varilla de longitud\(dx\) en posición\(x\). Tendrá una masa infinitesimal,\(dm\), dada por:\[\begin{aligned} dm = \mu(x) dx\end{aligned}\] La masa total de la vara es la entonces la suma (es decir, la integral) de los elementos de masa\[\begin{aligned} M = \int dm\end{aligned}\] y realmente podemos pensar en el\(\int\) signo como una suma, cuando se suman las cosas son infinitesimalmente pequeños. En la ecuación anterior, todavía no hemos especificado el\(x\) rango en el que queremos tomar la suma; es decir, necesitamos algún tipo de índice para que los elementos de masa hagan de esta una integral definida significativa. Como ya sabemos expresarnos\(dm\) en términos de\(dx\), podemos sustituir nuestra expresión por\(dm\) usar una con\(dx\):\[\begin{aligned} M = \int dm = \int_0^L \mu(x) dx\end{aligned}\] donde hemos hecho definida la integral especificando el rango sobre el cual sumar, ya que nosotros puede usar\(x\) para “etiquetar” los elementos de masa.

Cabe señalar que idear la integral anterior es la física. Resolverlo es matemática. Nos preocuparemos mucho más por escribir la integral que evaluar su valor. Evaluar la integral siempre puede ser realizada por un amigo matemático o una computadora, ¡pero determinar cuál integral escribir es el trabajo del físico!