28.4: El paquete Python de QExpy para física experimental

QExpy es un módulo Python que fue desarrollado con estudiantes de Queen's University para manejar todos los aspectos de los laboratorios de física de pregrado. En esta sección, analizamos cómo usar QExpy para propagar incertidumbres y trazar datos experimentales.

Propagación de incertidumbres

En el Capítulo 2, vimos cómo utilizar el “método derivado” para propagar la incertidumbre de las mediciones a la incertidumbre en un valor que dependía de esas mediciones. En el Ejemplo 2.3.2, propagamos las incertidumbres\(x = (3.00 ± 0.01)\text{m}\) y\(t = (0.76 ± 0.15)\text{s}\) a la cantidad\(k = \frac{t}{\sqrt{x}}\). A continuación mostramos la facilidad con la que se puede hacer esto con QexPy:

código python\(\PageIndex{1}\)

QExpy para propagar incertidumbres

#First, we load the QExpy module
import qexpy as q
#Now define our measurements with uncertainties:
t = q.Measurement(0.76, 0.15) # 0.76 +/- 0.15
x = q.Measurement(3, 0.1) # 3 +/- 0.1
#Now define k, which depends on t and x:
k = t/q.sqrt(x) #use the QExpy version of sqrt() since x is of type Measurement
#Print the result:
print(k)

Salida

0.44 +/- 0.09

que es el resultado que obtuvimos al aplicar manualmente el método derivado. Tenga en cuenta que utilizamos la función raíz cuadrada del módulo QExpy, ya que “sabe” cómo tomar la raíz cuadrada de un valor con incertidumbre (una “Medición” en el lenguaje de QExpy).

También vimos que cuando teníamos mediciones repetidas de la misma cantidad (Sección 2.3), se podía definir un valor central e incertidumbre para esa cantidad usando la media y las desviaciones estándar de las mediciones. QExpy puede tomar fácilmente un conjunto de mediciones (una matriz de valores) y convertirlas en una sola cantidad (una “Medida”) con un valor central e incertidumbre que corresponden a la media y desviación estándar del conjunto de mediciones:

código python\(\PageIndex{2}\)

QExpy para calcular la media y la desviación estándar

#First, we load the QExpy module
import qexpy as q
#We define $t$ as an array of values (note the square brackets):
t = q.Measurement([1.01, 0.76, 0.64, 0.73, 0.66])
#Choose the number of significant figures to print:
q.set_figs(2)
print("t=",t)

Salida

t = 0.76 +/- 0.15

Al usar QExpy, no necesitamos calcular tediosamente la media y la desviación estándar, como lo hicimos en el Ejemplo 2.3.1.

Trazado de datos experimentales con incertidumbres

En el Capítulo 2 habíamos presentado los datos en la Tabla A4.4.1 que correspondían a nuestras mediciones de cuánto tiempo tardó\((t)\) un objeto en caer una cierta distancia,\(x\). También habíamos introducido la Teoría de la gravedad de Chloe que predecía que los datos deberían ser descritos por el siguiente modelo:

\[\begin{aligned} t=k\sqrt{x}\end{aligned}\]

donde\(k\) fue una constante indeterminada de proporcionalidad.

\(x [\text{m}]\)	\(t [\text{s}]\)	\(\sqrt{x} [\text{m}^{\frac{1}{2}}]\)	\(k [\text{sm}^{-\frac{1}{2}}]\)
\ (x [\ texto {m}]\) ">\(1.00\)	\ (t [\ texto {s}]\) ">\(0.33\)	\ (\ sqrt {x} [\ texto {m} ^ {\ frac {1} {2}}]\) ">\(1.00\)	\ (k [\ texto {sm} ^ {-\ frac {1} {2}}]\) ">\(0.33\)
\ (x [\ texto {m}]\) ">\(2.00\)	\ (t [\ texto {s}]\) ">\(0.74\)	\ (\ sqrt {x} [\ texto {m} ^ {\ frac {1} {2}}]\) ">\(1.41\)	\ (k [\ texto {sm} ^ {-\ frac {1} {2}}]\) ">\(0.52\)
\ (x [\ texto {m}]\) ">\(3.00\)	\ (t [\ texto {s}]\) ">\(0.67\)	\ (\ sqrt {x} [\ texto {m} ^ {\ frac {1} {2}}]\) ">\(1.73\)	\ (k [\ texto {sm} ^ {-\ frac {1} {2}}]\) ">\(0.39\)
\ (x [\ texto {m}]\) ">\(4.00\)	\ (t [\ texto {s}]\) ">\(1.07\)	\ (\ sqrt {x} [\ texto {m} ^ {\ frac {1} {2}}]\) ">\(2.00\)	\ (k [\ texto {sm} ^ {-\ frac {1} {2}}]\) ">\(0.54\)
\ (x [\ texto {m}]\) ">\(5.00\)	\ (t [\ texto {s}]\) ">\(1.10\)	\ (\ sqrt {x} [\ texto {m} ^ {\ frac {1} {2}}]\) ">\(2.24\)	\ (k [\ texto {sm} ^ {-\ frac {1} {2}}]\) ">\(0.49\)

Cuadro A4.4.1: Mediciones de los tiempos de caída,\(t\), para que una bola de boliche caiga diferentes distancias,\(x\). También hemos calculado\(\sqrt{x}\) y el valor correspondiente de\(k\).

La forma más fácil de visualizar y analizar esos datos es trazarlos. En particular, si trazamos (gráfico)\(t\) versus\(\sqrt{x}\), esperamos que los puntos caigan en una línea recta que pasa por cero, con una pendiente de k (si los datos son descritos por la Teoría de Chloe). Podemos utilizar QExpy para graficar los datos así como determinar (“fit”) para la pendiente de la línea que mejor describa los datos, ya que esperamos que la pendiente corresponda al valor de\(k\). Al trazar datos y ajustarlos a una línea (u otra función), es importante asegurarse de que los valores tengan al menos una incertidumbre en la cantidad que se está trazando en el\(y\) eje. En este caso, hemos asumido que todas las mediciones del tiempo tienen una incertidumbre de\(0.15\text{s}\) y que las mediciones de la distancia no tienen (o despreciables) incertidumbres. El código python a continuación muestra cómo usar QExpy para trazar y ajustar los datos a una línea recta.

código python\(\PageIndex{3}\)

Uso de QExpy para trazar y ajustar datos lineales

#First, we load the QExpy module:
import qexpy as q

#Use matplotlib as the plot engine (try using 'bokeh' instead of 'mpl')
q.plot_engine = 'mpl'

#Set the number of significant figures to 2:
q.set_sigfigs(2)

#Then we enter the data:
#start with the values for the square root of height:
sqx = [1., 1.41, 1.73, 2., 2.24]

#and then, the corresponding times:
t = [0.33, 0.74, 0.67, 1.07, 1.1]

#Let us attribute an uncertainty of 0.15 to each measured values of t:
terr = 0.15

#We now make the plot. First, we create the plot object with the data
#Note that x and y refer to the x and y axes
fig = q.MakePlot(xdata = sqx, xname = "sqrt(distance)[m^0.5]", ydata = t, yerr = terr, yname = "time [s]", data_name = "My data")

#Ask QExpy to also determine the line of best fit.
fig.lit("linear")

#Then, we show it:
fig.show()

Salida

----------Fit results----------
Fit of My data to linear
Fit parameters:
My data_linear_fit0_fitpars_intercept = -0.24 +/- 0.22,
My data_linear_fit0_fitpars_slope = 0.61 +/- 0.13

Correlation matrix:
[[ 1.      -0.968]
 [-0.968   1.    ]]
 chi/2ndof = 2.04/2
 ----------End fit results----------

Figura A4.4.1: Gráfica QExpy de\(t\) versus\(\sqrt{x}\) y línea de mejor ajuste.

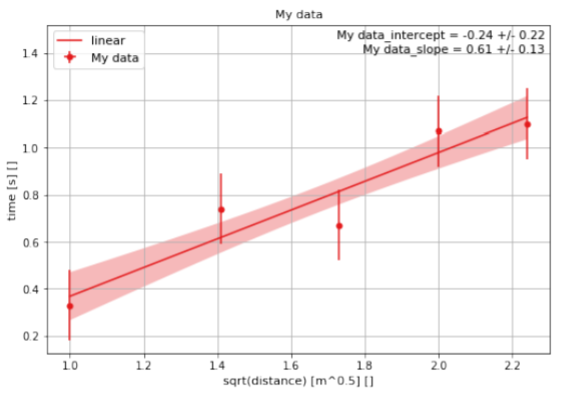
La gráfica de la Figura A4.4.1 muestra que los puntos de datos son consistentes con caer en línea recta, cuando se toman en cuenta sus barras de error. También hemos pedido a QExpy que nos muestre la línea que mejor se ajusta a los datos, representada por la línea con el área sombreada. Cuando preguntamos por la línea de mejor ajuste, QExpy no sólo dibujó la línea, sino que también nos dio los valores e incertidumbres para la pendiente y la intersección de la línea. El área sombreada alrededor de la línea corresponde a otras posibles líneas que se obtendrían utilizando diferentes valores de la pendiente e interceptar dentro de sus correspondientes incertidumbres. La salida también proporciona una línea que nos dice que chi2/ndof = 2.04/2; aunque no es necesario entender los detalles, esta es una medida de qué tan bien se describen los datos por la línea de mejor ajuste. Generalmente, se supone que el ajuste es “bueno” si esta relación es cercana a 1 (la relación se llama “el chi-cuadrado reducido”). La “matriz de correlación” nos dice cómo se vincula el mejor valor de ajuste de la pendiente con el mejor valor de ajuste de la intersección, del que no necesita preocuparse aquí.

Ya que esperamos que la pendiente de los datos sea k, esto nos proporciona un método para determinar k a partir de los datos as\((0.61 ± 0.13) \text{sm}^{−\frac{1}{2}}\). Realizar un ajuste lineal de los datos es la mejor manera de determinar una constante de proporcionalidad entre las mediciones. Por último, esperamos que la intercepción sea igual a cero según nuestro modelo. La línea de mejor ajuste de QExPy tiene una intercepción de\((−0.24 ± 0.22)\text{s}\), que está ligeramente por debajo, pero consistente, con cero. A partir de estos datos, concluimos que las mediciones son consistentes con la Teoría de Chloe.