11.4.2: Argumentos, consecuencias lógicas y contraejemplos

Última actualización
Guardar como PDF

Page ID: 101937

Bradley H. Dowden
California State University Sacramento

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Pasemos de la semántica de las oraciones a la semántica de los argumentos. Se dice que un argumento en Lógica Sentencial es válido o lógicamente correcto por si acaso la conclusión debe ser cierta cuando las premisas son verdaderas. Cuando este es el caso con algún argumento, decimos que su conclusión es una consecuencia lógica de sus premisas. Aquí hay un argumento válido:

A → D
A
—
D

Aquí hay una receta o método mecánico para decidir si un argumento es válido. Verifique la tabla de verdad para todas las oraciones del argumento (es decir, todas sus premisas más su conclusión). Si en todas las situaciones (es decir, todas las filas, o todas las asignaciones de valores de verdad a las letras mayúsculas) que hagan que las premisas sean verdaderas, la conclusión también se hace verdadera, entonces los declaran válido el argumento. En caso contrario, declararlo inválido. Apliquemos el método a esta tabla de verdad para el argumento anterior:

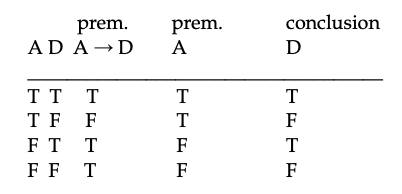
Captura de pantalla 2019-12-25 a las 5.15.27 PM.png

Cualquier argumento escrito en Lógica Sentencial formal puede ser verificado para su validez por este método de construcción e inspección de tablas de verdad. Un argumento inválido tendrá una fila que muestre cómo todas las premisas podrían ser verdaderas mientras la conclusión sea falsa.

Ejercicio\(\PageIndex{1}\)

Utilice el método de la tabla de verdad para probar si este argumento es válido.

~A
C → A
—
~C

Responder: Sí, es válido. Tiene la forma de modus tollens. No hay manera de que las premisas sean ciertas mientras la conclusión sea falsa sin violar las tablas de la verdad.

En un argumento válido, no hay fila de la tabla de la verdad en la que las premisas obtengan Ts mientras que la conclusión obtiene una F. Es decir, los argumentos válidos no tienen contraejemplos. Observe que los argumentos válidos pueden tener premisas falsas.

Ejercicio\(\PageIndex{1}\)

¿Este argumento tiene un contraejemplo?

A → B
B
—
A

Responder: Sí. Este argumento tiene la forma inválida llamada afirmación de lo consecuente. En una situación en la que A es falsa y B es verdadera, tenemos un contraejemplo porque entonces el argumento tiene verdaderas premisas y una conclusión falsa. Por ejemplo, aquí hay un argumento que comete la falacia de afirmar lo consecuente: Si ese chico parado ahí es tu abuelo, entonces ese chico es un varón. Ese chico es un varón. Entonces, ese chico parado ahí es tu abuelo. Esto tiene verdaderas premisas y una conclusión falsa en cualquier situación en la que haya un chico parado ahí. Ya que hay una situación, aunque no sea una situación en la vida real, eso haría que las premisas fueran verdaderas y la conclusión falsa, el argumento no es válido.