12.2: Uso de diagramas de Venn-Euler para probar la invalidez

En la lógica de clases, podemos crear diagramas que nos ayuden a probar argumentos de validez. Antes de hacer esto, sin embargo, vamos a mejorar nuestra habilidad de razonamiento con el complemento de clases, es decir, el conjunto de todas las cosas no en una clase. Si eres estadounidense, entonces ¿cuál es nuestro nombre para los no americanos? Es “extranjero”. Cuanto más viajan los estadounidenses, más conocen a los no estadounidenses.

Suponiendo que nadie puede ser tanto judío como cristiano, sería cierto decir que todos los judíos son no cristianos y verdad decir que algunos no judíos son no cristianos, pero sería falso decir que todos los no cristianos son judíos y falso decir que todos los no cristianos son no judíos. ¡Uf! Enhorabuena y cumplidos si pudieras comprender cuidadosamente las complejidades de esas complementaciones sobre las clases. Si pudieras, puedes completar esta comprobación de concepto correctamente.

Ejercicio\(\PageIndex{1}\)

Martin (en la foto de arriba) no es un macho blanco si Martin es

a. un no macho blanco.
b. un macho no blanco,
c. un no macho no blanco.
d. cualquiera de los anteriores.

Contestar

Respuesta (d). Responder preguntas como esta sería mucho más fácil si tuviéramos algún tipo de método de imagen o diagrama que nos mostrara lo que está pasando. A lo mejor puedas inventar uno. Euler intentó hacer esto allá por el siglo XVIII en Suiza.

La habilidad para negar términos es necesaria para construir diagramas de Venn-Euler. Este método de diagramación es una manera útil de evaluar rápidamente la validez deductiva de los argumentos en la lógica de clase. Puede guiarte a la valoración correcta cuando el argumento es demasiado intrincado para analizarlo en tu cabeza. Al presentar este método, primero introduciremos los diagramas para las clases, luego generalizaremos el método para que pueda usarse para mostrar si las oraciones sobre las clases son verdaderas o falsas, y luego generalizar nuevamente el método para que pueda usarse para mostrar si los argumentos que utilizan estas oraciones son deductivamente válido.

El círculo de abajo es el diagrama de Euler de la clase de manzanas.

r

En este diagrama bidimensional, cualquier punto dentro del círculo representa una manzana y cualquier punto fuera del círculo representa una no manzana como un musulmán o un lápiz. La costumbre para el etiquetado es usar una mayúscula para iniciar el nombre de una región (clase) y una minúscula letra para nombrar a un miembro específico de una región (clase). La letra minúscula “r” etiqueta el punto a la derecha del círculo que representa a una no manzana específica, digamos Thomas Edison, el inventor estadounidense y fundador de General Electric Corporation. No hay nada importante en la forma de la región. Una elipse o un rectángulo estaría bien, siempre y cuando quede claro qué hay en la región y lo que está fuera, es decir, qué hay en la clase y qué no. El tamaño del círculo tampoco es importante. Tampoco prestamos atención a mover el diagrama hacia la izquierda o hacia la derecha o hacia arriba o hacia abajo. Todos esos cambios producirían el mismo diagrama, en lo que respecta a la lógica de clases.

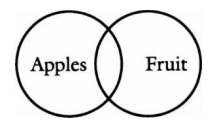
El siguiente es un diagrama más complicado que representa tanto la clase de manzanas como la clase de fruta. En el mundo real, la clase de manzanas está incluida completamente dentro de la clase más grande de fruta. El diagrama proporciona una imagen de esta relación del mundo real:

El diagrama anterior representa la verdad de la frase “Todas las manzanas son frutas”, pero eres bienvenido a dibujar diagramas que no imaginen como es el mundo.

Cualquier etiqueta para una región puede estar dentro o fuera de ella, siempre que no haya ambigüedad sobre qué etiqueta va con qué región. A veces llamaremos “círculos” a las regiones ovales ya que no prestamos ninguna atención a la diferencia entre un círculo y una elipse.

Aquí hay un diagrama de Euler en el que son ciertas las afirmaciones de la forma “No A son B”:

Lo importante de este diagrama es que los dos círculos no se crucen (se superpongan). Los círculos tampoco deberían ser tangentes, porque eso dificultaría saber si las dos clases tienen un miembro común.

Aquí hay un diagrama de Venn que muestra la misma información, pero de manera menos intuitiva:

En un diagrama de Venn, todos los círculos deben superponerse mutuamente. Esto no es obligatorio con los diagramas de Euler. Considere los puntos x, y y z en el siguiente diagrama. Las clases A y B se cruzan, es decir, tienen miembros en común. Uno de esos miembros es y.

El punto x no está ni en la clase A ni en la clase B. Está en el complemento de cada uno. El punto y está tanto en A como en B. El punto z está en B pero no en A. Al ver el diagrama, se puede ver que algunos miembros de B están en A y otros no. Sin embargo, no se puede decir si A tiene más miembros que B. Si la región A es mayor que B en un diagrama, no se puede decir si A tiene más miembros que B. Para el caso, ni siquiera se puede decir si la clase tiene algún miembro en absoluto. No obstante, en todos los diagramas a partir de ahora, asumiremos que estamos comenzando con clases que no están vacías.

Aquí hay un diagrama que representa la relación del mundo real entre manzanas, frutas, naranjas, manzanas en París, manzanas en restaurantes en París y frutas propiedad de nuestro amigo Juan:

Para ser claros, siempre usaremos letras mayúsculas o palabras en mayúscula para clases de cosas. Si queremos agregar la información de que algún objeto específico es miembro de una de las clases, usaremos una letra minúscula para representar al miembro. En el diagrama anterior la a minúscula representa la una manzana en mi refrigerador. Se puede ver que la letra a está fuera del círculo P; esto demuestra que la manzana en mi refrigerador no está en París. Observe que el propio Juan no es miembro de ninguna de las clases del diagrama anterior; la información sobre Juan está incrustada en la definición de J. Al inspeccionar el diagrama se puede decir que Juan no es dueño de ninguna manzana parisina (porque J y P no se superponen), pero sí es dueño de manzanas (porque J se cruza con A), posee naranjas (porque J cruza O), y posee algún otro fruto no especificado (porque J está en F pero no todo J está en A u O).

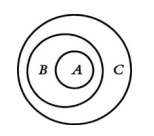
Que A = ciudadanos estadounidenses que viven en la ciudad de Nueva York, B = habitantes de la ciudad, C = estadounidenses. Aquí hay un diagrama de Euler que muestra sus relaciones en el mundo real.

A continuación se explica cómo mostrar las mismas relaciones con un diagrama de Venn:

En los diagramas de Venn, las áreas sombreadas son el conjunto vacío; no contienen nada. Con la técnica de Venn aplicada a tres conjuntos, los tres círculos deben cruzarse mutuamente, a diferencia de los diagramas de Euler.

¿Cómo dibujarías un diagrama en el que la afirmación de que algunas manzanas son de Canadá y otras no son es cierta? Esto va a hacer el truco:

C = la clase de cosas de Canadá

A = la clase de manzanas

El patrón de oraciones “Todos A son no-B” es cierto en el siguiente diagrama:

Observe que es el mismo que el diagrama que dibujarías para “No A son B.” Las oraciones lógicamente equivalentes tienen el mismo tipo de diagramas. Esa es una idea clave en la lógica de clase.

El diagrama anterior representaría la frase falsa “No tejanos son americanos” si se utilizara el siguiente diccionario:

A = Texanos
B = Americanos

Si bien esa frase es falsa en el mundo real, el diagrama muestra cómo sería el mundo si la oración fuera cierta. El mismo punto se hace diciendo que el diagrama es una imagen de lo que es cierto en un cierto “mundo posible” que no es el mundo real.

Ejercicio\(\PageIndex{1}\)

Hacer que la afirmación “Todos los tejanos son no estadounidenses” sea cierta en un diagrama, usando el diccionario anterior para A y B.

Contestar

Observe que en este diagrama cada tejano A está fuera de América B y por lo tanto es un no americano. Entonces este mundo posible no es el mundo real.

Dejar que A sea la clase de las manzanas. En los dos diagramas de abajo la frase “Todas las manzanas son plátanos” es cierta (aunque la oración sea falsa en el mundo real):

Pero fíjense la diferencia en los dos diagramas. En el de la izquierda algunos plátanos no logran ser manzanas. Esto no es así en el diagrama de la derecha. En el segundo diagrama, la clase de manzanas y la clase de plátanos son la misma clase. Un diagrama de las relaciones del mundo real entre manzanas y plátanos se vería así:

Ejercicio\(\PageIndex{1}\)

Dibuja un diagrama para manzanas y frutas en el que la siguiente frase no sea cierta en el diagrama: “Todas las manzanas son frutas”. La frase es cierta en el mundo real, pero no será en el mundo posible representado por tu diagrama.

Contestar

Hay más de un tipo de diagrama que funcionará.

Con una frase como “Todas las manzanas son frutas”, el analista tiene la opción de tratarla en la lógica de clase o en la lógica sentencial. En la lógica de clases, es lógicamente equivalente a “Todas las cosas en la clase de las manzanas son también cosas de la clase de la fruta”. Esto establece una relación entre dos clases. En la lógica sentencial, la oración es lógicamente equivalente a “Si es una manzana, entonces es un fruto”. Esto establece una relación condicional entre dos suboraciones.

Ahora podemos generalizar el método diagrama a una técnica para evaluar la validez deductiva de los argumentos, siempre que las oraciones que constituyen el argumento describan cómo las clases de objetos se relacionan entre sí. El método del diagrama Venn-Euler para evaluar argumentos funciona solo para argumentos deductivos en la lógica de clase. Muestra un argumento para ser válido si no hay diagrama de un contraejemplo al argumento. Por definición, el contraejemplo de un argumento es una posible situación o una interpretación del argumento que muestra cómo podría tener verdaderas premisas y una conclusión falsa.

Más específicamente, aquí es cómo aplicar el método de verificación de validez en la lógica de clase:

Traducir las premisas y la conclusión del argumento en frases apropiadas de lógica de clase. Busca un contraejemplo. Es decir, tratar de trazar estas oraciones en lógica de clase para que las premisas salgan verdaderas en el diagrama y la conclusión salga falsa en el diagrama. Si hay un diagrama como este, entonces este diagrama de contraejemplo muestra que el argumento es deductivamente inválido. Sin embargo, si todos los diagramas posibles no logran producir un contraejemplo, entonces se declara que el argumento es deductivamente válido.

Este método nunca da una respuesta incorrecta si realmente ha examinado correctamente todos los diagramas posibles. Un argumento es válido si no existe un contraejemplo, no simplemente si no se puede encontrar uno. A lo mejor no puedes encontrar uno porque no miraste con cuidado. Entonces, la aplicación del método de diagramas Venn-Euler es riesgosa ya que su respuesta depende de que seas correcto cuando dices que has mirado y estás seguro de que no existe un contraejemplo.

Para ver la técnica en acción, probémosla en este patrón de argumento:

No A son B.
No C son B.
Entonces, No A son C.

Aquí hay un diagrama que hace que todas las premisas sean ciertas:

Ninguno de los círculos se cruzan o están contenidos dentro de otro. En este diagrama la conclusión es cierta. ¿Podemos concluir que el patrón argumental es válido? No, no a partir de esta información. En cambio, deberíamos haber estado buscando para asegurarnos de que no existe un diagrama que haga verdaderas las premisas sino que la conclusión sea falsa. De hecho, existe tal diagrama:

Aquí la conclusión es falsa cuando las premisas son verdaderas, señal delatora de invalidez. Por lo tanto, el método diagram declara que el argumento pattern no es válido.

Ejercicio\(\PageIndex{1}\)

Utilice el método diagram para mostrar la validez de este patrón de argumentos:

Todas A son B.
Todas las B son C.
Entonces, Todas A son C.

Contestar

Aquí hay una manera de dibujar un diagrama de ambas premisas siendo verdaderas

Puede haber otros diagramas de las premisas: permitir que el círculo A sea igual al círculo B, o para que B sea igual a C. Sin embargo, en todos los diagramas posibles de las premisas, la conclusión sale cierta en el diagrama. Entonces, no se puede producir contraejemplo. Por lo tanto, la técnica Venn-Euler declara válido este patrón de argumento.

Ejercicio\(\PageIndex{1}\)

Utilizar la técnica de diagrama para evaluar la validez o invalidez de este argumento. Interpreta algunos para que signifiquen “al menos uno y quizás todos”.

Algunos gatos son felinos.
Algunos animales son felinos.
Entonces, algunos animales son gatos.

Contestar

El argumento no es válido; el siguiente diagrama sirve como contraejemplo:

Algunos C son F.
Algunos A son F.
Algunos A son C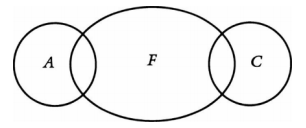

Al tratar de encontrar la forma lógica de un argumento, no siempre es posible decir si se debe buscar su forma en la lógica de clase o en la lógica sentencial. Experimenta para ver qué va a funcionar. Algunos argumentos tienen formas lógicas que no se pueden expresar adecuadamente de ninguna manera, y entonces se deben llevar a cabo lógicas más poderosas como la lógica del predicado sobre el argumento.

Además, algunos argumentos son deductivamente válidos aunque su validez no es una cuestión de forma lógica utilizando ninguna lógica formal. Aquí hay un ejemplo:

John es soltero.
Entonces, no está casado.

La validez se debe no sólo a la forma, sino al contenido —en particular, al hecho de que la definición de licenciatura implica que todos los solteros no están casados. Podríamos forzar que este argumento sea válido debido a su forma lógica en la lógica de clase si pudiéramos codificar la idea de que todos los solteros no están casados en la lógica de clase, y nosotros podemos. Solo agrega la premisa: Todos los solteros no están casados. Los argumentos válidos que no necesitan la inserción de definiciones se denominan formalmente válidos. Todos los argumentos formalmente válidos son deductivamente válidos, pero lo contrario no se sostiene. No obstante, en nuestro curso no vamos a prestar atención a esta fina distinción. Si ve que se necesita una definición para que el argumento sea válido, continúe e insértelo y no se preocupe por el hecho de que esto demuestre que su argumento es deductivamente válido pero no válido formalmente.

Los diagramas de Venn-Euler tienen otros usos además de verificar su validez. Si dos oraciones pueden tener el mismo diagrama, entonces son lógicamente equivalentes en lógica de clase. Los diagramas también se pueden usar para verificar la consistencia. Si hay un diagrama en el que cada oración de un conjunto de oraciones sale verdadera, entonces el conjunto es lógicamente consistente.