7.2: El Cálculo Secuente

Última actualización
Guardar como PDF

Page ID: 103522

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Mientras que muchos sistemas de derivación operan con arreglos de oraciones, el cálculo secuencial opera con secuentes. Un secuente es una expresión de la forma\[A_1, \dots, A_m \Sequent B_1, \dots, B_m,\nonumber\] que es un par de secuencias de oraciones, separadas por el símbolo secuente\(\Sequent\). Cualquiera de las secuencias puede estar vacía. Una derivación en el cálculo secuente es un árbol de secuentes, donde los secuentes superiores son de una forma especial (se llaman “secuentes iniciales” o “axiomas”) y cada otro secuente se desprende de los secuentes inmediatamente por encima de él por una de las reglas de inferencia. Las reglas de inferencia manipulan las oraciones en los secuentes (agregándolas, quitándolas o reordenándolas a la izquierda o a la derecha), o introducen una fórmula compleja en la conclusión de la regla. Por ejemplo, la\(\LeftR{\land}\) regla permite la inferencia de\(A, \Gamma \Sequent \Delta\) a\(A \land B, \Gamma \Sequent \Delta\), y la\(\RightR{\lif}\) permite la inferencia de\(A, \Gamma \Sequent \Delta, B\) a\(\Gamma \Sequent \Delta, A \lif B\), para cualquier\(\Gamma\)\(\Delta\), \(A\), y\(B\). (En particular,\(\Gamma\) y\(\Delta\) puede estar vacío.)

La\(\Proves\) relación basada en el cálculo secuente se define de la siguiente manera:\(\Gamma \Proves A\) si hay alguna secuencia\(\Gamma_0\) tal que cada\(A\) in\(\Gamma_0\) está adentro\(\Gamma\) y hay una derivación con la secuencia \(\Gamma_0 \Sequent A\)en su raíz. \(A\)es un teorema en el cálculo secuencial si el secuente\(\Sequent A\) tiene una derivación. Por ejemplo, aquí hay una derivación que muestra que\(\Proves (A \land B) \lif A\):

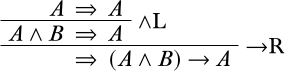
7.2.1.png

Un conjunto\(\Gamma\) es inconsistente en el cálculo secuencial si hay una derivación de\(\Gamma_0 \Sequent\) (donde cada\(A \in \Gamma_0\) está adentro\(\Gamma\) y el lado derecho del secuente está vacío). Usando la regla\(\RightR{\Weakening}\), cualquier oración puede derivarse de un conjunto inconsistente.

El cálculo secuente fue inventado en la década de 1930 por Gerhard Gentzen. Por su diseño sistemático y simétrico, es un formalismo muy útil para desarrollar una teoría de derivaciones. Es relativamente fácil encontrar derivaciones en el cálculo secuencial, pero estas derivaciones suelen ser difíciles de leer y su conexión con las pruebas a veces no es fácil de ver. Sin embargo, ha demostrado ser un enfoque muy elegante para los sistemas de derivación y muchas lógicas tienen sistemas de cálculo secuentes.