8.3: Reglas del cuantificador

Última actualización
Guardar como PDF

Page ID: 103629

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Reglas para\(\lforall{}{}\)

8.3.1.png

En\(\LeftR{\lforall{}{}}\),\(t\) es un término cerrado (es decir, uno sin variables). En\(\RightR{\lforall{}{}}\),\(a\) es un símbolo constante que no debe ocurrir en ninguna parte del secuente inferior de la\(\RightR{\lforall{}{}}\) regla. Llamamos a\(a\) la variable propia de la\(\RightR{\forall}\) inferencia.

Reglas para\(\lexists{}{}\)

8.3.2.png

Nuevamente,\(t\) es un término cerrado, y\(a\) es un símbolo constante que no ocurre en el secuente inferior de la\(\LeftR{\lexists{}{}}\) regla. Llamamos a\(a\) la variable propia de la\(\LeftR{\lexists{}{}}\) inferencia.

La condición de que una variable propia no ocurra en el secuente inferior de la\(\RightR{\lforall{}{}}\) o\(\LeftR{\lexists{}{}}\) inferencia se denomina condición de variable propia.

Utilizamos el término “variable propia” a pesar de que\(a\) en las reglas anteriores es un símbolo constante. Esto tiene razones históricas.

En\(\RightR{\lexists{}{}}\) y no\(\LeftR{\lforall{}{}}\) hay restricciones sobre el término\(t\). Por otro lado, en las\(\RightR{\lforall{}{}}\) reglas\(\LeftR{\lexists{}{}}\) y, la condición de variable propia requiere que el símbolo constante\(a\) no se presente en ningún lugar fuera de\(A(a)\) en el secuente superior. Es necesario asegurar que el sistema sea sano, es decir, sólo deriva secuentes que sean válidos. Sin esta condición, se permitiría lo siguiente:

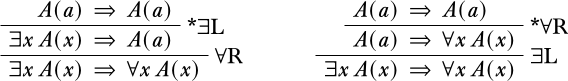
8.3.3.png

Sin embargo, no\(\lexists{x}{A(x)} \Sequent \lforall{x}{A(x)}\) es válido.