8.7: Derivaciones con cuantificadores
- Page ID
- 103655
Ejemplo\(\PageIndex{1}\)
Dar una\(\Log{LK}\) -derivación del secuente\(\lexists{x}{\lnot A(x)} \Sequent \lnot \lforall{x}{A(x)}\).
Al tratar con cuantificadores, tenemos que asegurarnos de no violar la condición de variable propia, y a veces esto nos obliga a jugar con el orden de llevar a cabo ciertas inferencias. En general, ayuda a tratar de cuidar primero las reglas sujetas a la condición de variable propia (serán más bajas en la prueba terminada). Además, es una buena idea tratar de mirar hacia adelante y tratar de adivinar cómo podría ser el secuente inicial. En nuestro caso, tendrá que ser algo así como\(A(a) \Sequent A(a)\). Eso quiere decir que cuando estemos “invirtiendo” las reglas del cuantificador, tendremos que elegir el mismo término —lo que llamaremos\(a\) — tanto para la\(\lforall{}{}\) regla como para la\(\lexists{}{}\) regla. Si escogiéramos términos diferentes para cada regla, terminaríamos con algo así como\(A(a) \Sequent A(b)\), que por supuesto, no es derivable.
Comenzando como de costumbre, escribimos
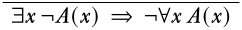
Podríamos o llevar a cabo la\(\LeftR{\exists}\) regla o la\(\RightR{\lnot}\) regla. Dado que la\(\LeftR{\exists}\) regla está sujeta a la condición de variable propia, es una buena idea cuidarla más temprano que tarde, así que primero haremos esa.
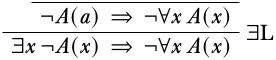
Aplicando las\(\RightR{\lnot}\) reglas\(\LeftR{\lnot}\) y al revés, obtenemos
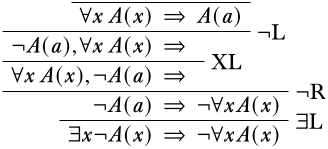
En este punto, nuestra única opción es llevar a cabo la\(\LeftR{\forall}\) regla. Ya que esta regla no está sujeta a la restricción de la variable propia, estamos en claro. Recuerda, queremos intentar obtener un secuente inicial (de la forma\(A(a) \Sequent A(a)\)), por lo que debemos elegir\(a\) como nuestro argumento para\(A\) cuando aplicamos la regla.
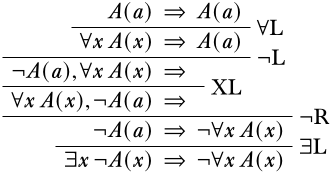
Es importante, especialmente cuando se trata de cuantificadores, verificar en este punto que no se ha violado la condición de variable propia. Dado que la única regla que aplicamos que está sujeta a la condición de variable\(\LeftR{\exists}\) propia fue, y la variable propia\(a\) no ocurre en su secuente inferior (el secuenciante final), esta es una derivación correcta.
Problema\(\PageIndex{1}\)
Dar derivaciones de los siguientes secuentes:
-
\(\lforall{x}{(A(x) \lif B)} \Sequent (\lexists{y}{A(y)} \lif B)\)
-
\(\lexists{x}{(A(x) \lif \lforall{y}{A(y)})}\)


