9.7: Nociones teóricas de prueba

Última actualización
Guardar como PDF

Page ID: 103642

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Así como hemos definido una serie de nociones semánticas importantes (validez, vinculación, satisfacción), ahora definimos nociones teóricas de prueba correspondientes. Éstas no se definen por la apelación a la satisfacción de sentencias en estructuras, sino por la apelación a la derivabilidad o no derivabilidad de ciertas oraciones de otras. Fue un descubrimiento importante que estas nociones coincidan. Lo que hacen es el contenido de los teoremas de solidez e integridad.

Definición\(\PageIndex{1}\): Theorems

Una oración\(A\) es un teorema si existe una derivación de\(A\) en deducción natural en la que se descargan todos los supuestos. Escribimos\(\Proves A\) si\(A\) es un teorema y\(\ProvesN A\) si no lo es.

Definición\(\PageIndex{2}\): Derivability

Una oración\(A\) es derivable de un conjunto de oraciones\(\Gamma\),\(\Gamma \Proves A\), si hay una derivación con conclusión\(A\) y en la que cada suposición es descargada o está en\(\Gamma\). Si no\(A\) es derivable de\(\Gamma\) escribimos\(\Gamma \ProvesN A\).

Definición\(\PageIndex{3}\): Consistency

Un conjunto de oraciones\(\Gamma\) es inconsistente iff\(\Gamma \Proves \lfalse\). Si no\(\Gamma\) es inconsistente, es decir\(\Gamma \ProvesN \lfalse\), si, decimos que es consistente.

Proposición\(\PageIndex{1}\): Reflexivity

Si\(A \in \Gamma\), entonces\(\Gamma \Proves A\).

Prueba. La suposición\(A\) por sí misma es una derivación de\(A\) donde se encuentra cada suposición no descargada (es decir,\(A\))\(\Gamma\). ◻

Proposición\(\PageIndex{2}\): Monotony

Si\(\Gamma \subseteq \Delta\) y\(\Gamma \Proves A\), entonces\(\Delta \Proves A\).

Prueba. Cualquier derivación\(A\) de\(\Gamma\) es también una derivación\(A\) de\(\Delta\). ◻

Proposición\(\PageIndex{3}\): Transitivity

Si\(\Gamma \Proves A\) y\(\{A\} \cup \Delta \Proves B\), entonces\(\Gamma \cup \Delta \Proves B\).

Prueba. Si\(\Gamma \Proves A\), hay una derivación\(\delta_0\) de\(A\) con todos los supuestos no descargados en\(\Gamma\). Si\(\{A\} \cup \Delta \Proves B\), entonces hay una derivación\(\delta_1\) de\(B\) con todos los supuestos no descargados en\(\{A\} \cup \Delta\). Ahora considere:

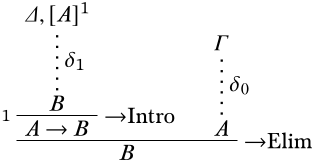
9.7.1.png

Los supuestos no descargados están ahora todos entre\(\Gamma \cup \Delta\), así que esto demuestra\(\Gamma \cup \Delta \Proves B\). ◻

Cuando\(\Gamma = \{A_1, A_2, \ldots, A_k\}\) es un conjunto finito podemos usar la notación simplificada\(A_1,A_2,\ldots,A_k \Proves B\) para\(\Gamma \Proves B\), en particular\(A \Proves B\) significa que\(\{A\} \Proves B\).

Tenga en cuenta que si\(\Gamma \Proves A\) y\(A \Proves B\), entonces\(\Gamma \Proves B\). De ello se deduce también que si\(A_1, \dots, A_n \Proves B\) y\(\Gamma \Proves A_i\) para cada uno\(i\), entonces\(\Gamma \Proves B\).

Proposición\(\PageIndex{4}\)

Los siguientes son equivalentes.

\(\Gamma\)es inconsistente.
\(\Gamma \Proves {A}\)por cada oración\({A}\).
\(\Gamma \Proves {A}\)y\(\Gamma \Proves \lnot {A}\) para alguna sentencia\({A}\).

Prueba. Ejercicio. ◻

Problema\(\PageIndex{1}\)

Probar Proposición\(\PageIndex{4}\).

Proposición\(\PageIndex{5}\): Compactness

Si\(\Gamma \Proves A\) entonces hay un subconjunto finito\(\Gamma_0 \subseteq \Gamma\) tal que\(\Gamma_0 \Proves A\).
Si cada subconjunto finito de\(\Gamma\) es consistente, entonces\(\Gamma\) es consistente.

Prueba.

Si\(\Gamma \Proves A\), entonces hay una derivación\(\delta\)\(A\) de\(\Gamma\). \(\Gamma_0\)Sea el conjunto de supuestos no descargados de\(\delta\). Dado que cualquier derivación es finita, sólo\(\Gamma_0\) puede contener finitamente muchas oraciones. Entonces,\(\delta\) es una derivación\(A\) de una finita\(\Gamma_0 \subseteq \Gamma\).
Este es el contrapositivo de (1) para el caso especial\(A \ident \lfalse\).

◻