9.9: Derivabilidad y los conectivos proposicionales

Última actualización
Guardar como PDF

Page ID: 103618

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Proposición\(\PageIndex{1}\)

Ambos\(A \land B \Proves A\) y\(A \land B \Proves B\)
\(A, B \Proves A \land B\).

Comprobante.

Podemos derivar tanto
Podemos derivar:

◻

Proposición\(\PageIndex{2}\)

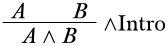
\(A \lor B, \lnot A, \lnot B\)es inconsistente.
Ambos\(A \Proves A \lor B\) y\(B \Proves A \lor B\).

Comprobante.

Considere la siguiente derivación:

Esta es una derivación\(\lfalse\) de supuestos no descargados\(A \lor B\),\(\lnot A\), y\(\lnot B\).
Podemos derivar tanto

◻

Proposición\(\PageIndex{3}\)

\(A, A \lif B \Proves B\).
Ambos\(\lnot A \Proves A \lif B\) y\(B \Proves A \lif B\).

Comprobante.

Podemos derivar:
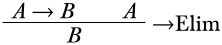
Esto se muestra por las dos derivaciones siguientes:

Tenga en cuenta que\(\Intro{\lif}\) puede, pero no tiene que, descargar el supuesto\(A\).

◻