9.13: Validez con predicado de identidad

Última actualización
Guardar como PDF

Page ID: 103660

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Template:MathJaxZach

Proposición\(\PageIndex{1}\)

La deducción natural con reglas para\(\eq[][]\) es sólida.

Prueba. Cualquier fórmula de la forma\(\eq[t][t]\) es válida, ya que para cada estructura\(\Struct M\),\(\Sat{M}{\eq[t][t]}\). (Obsérvese que asumimos que el término\(t\) es molido, es decir, no contiene variables, por lo que las asignaciones de variables son irrelevantes).

Supongamos que la última inferencia en una derivación es\(\Elim{\eq[][]}\), es decir, la derivación tiene la siguiente forma:

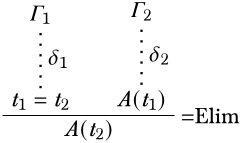
9.13.1.png

Las premisas\(\eq[t_1][t_2]\) y\(A(t_1)\) se derivan de supuestos no descargados\(\Gamma_1\) y\(\Gamma_2\), respectivamente. Queremos mostrar que se\(A(t_2)\) desprende de\(\Gamma_1 \cup \Gamma_2\). Considerar una estructura\(\Struct{M}\) con\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\). Por hipótesis de inducción,\(\Sat{M}{A(t_1)}\) y\(\Sat{M}{\eq[t_1][t_2]}\). Por lo tanto,\(\Value{t_1}{M} = \Value{t_2}{M}\). Dejar\(s\) ser cualquier asignación de variable, y\(s'\) ser la\(x\) -variante dada por\(s'(x) = \Value{t_1}{M} = \Value{t_2}{M}\). Por Proposición 5.13.3,\(\Sat[,s]{M}{A(t_1)}\) iff\(\Sat[,s']{M}{A(x)}\) iff\(\Sat[,s]{M}{A(t_2)}\). Ya que\(\Sat{M}{A(t_1)}\), tenemos\(\Sat{M}{A(t_2)}\). ◻