12.1: Introducción
- Page ID
- 103668
¿Qué significa para una función, digamos, de\(\Nat\)\(\Nat\) a para ser computable? Entre las primeras respuestas, y la más conocida, está que una función es computable si puede ser computada por una máquina Turing. Esta noción fue planteada por Alan Turing en 1936. Las máquinas de Turing son un ejemplo de un modelo de computación, son una forma matemáticamente precisa de definir la idea de un “procedimiento computacional”. Se debate qué significa exactamente eso, pero es ampliamente aceptado que las máquinas Turing son una forma de especificar procedimientos computacionales. A pesar de que el término “máquina de Turing” evoca la imagen de una máquina física con partes móviles, estrictamente hablando una máquina de Turing es una construcción puramente matemática, y como tal idealiza la idea de un procedimiento computacional. Por ejemplo, no ponemos ninguna restricción en los requisitos de tiempo o memoria de una máquina Turing: las máquinas Turing pueden calcular algo incluso si el cálculo requeriría más espacio de almacenamiento o más pasos de los que hay átomos en el universo.
Quizás sea mejor pensar en una máquina de Turing como un programa para un tipo especial de mecanismo imaginario. Este mecanismo consiste en una cinta y un cabezal de lectura-escritura. En nuestra versión de las máquinas Turing, la cinta es infinita en una dirección (hacia la derecha), y se divide en cuadrados, cada uno de los cuales puede contener un símbolo de un alfabeto finito. Dichos alfabetos pueden contener cualquier número de símbolos diferentes, digamos, pero principalmente nos conformaremos con tres:\(\TMendtape\),\(\TMblank\), y\(\TMstroke\). Cuando se inicia el mecanismo, la cinta está vacía (es decir, cada cuadrado contiene el símbolo\(\TMblank\)) excepto el cuadrado más a la izquierda, que contiene\(\TMendtape\), y un número finito de cuadrados que contienen la entrada. En cualquier momento, el mecanismo se encuentra en uno de un número finito de estados. Al inicio, la cabeza escanea el cuadrado más a la izquierda y en un estado inicial especificado. En cada paso de la ejecución del mecanismo, el contenido del cuadrado actualmente escaneado junto con el estado en el que se encuentra el mecanismo y el programa de la máquina Turing determinan qué sucede después. El programa de la máquina Turing viene dado por una función parcial que toma como entrada un estado\(q\) y un símbolo\(\sigma\) y emite un triple\(\tuple{q', \sigma', D}\). Siempre que el mecanismo esté en estado\(q\) y lea símbolo\(\sigma\), reemplaza el símbolo en el cuadrado actual por\(\sigma'\), la cabeza se mueve a la izquierda, a la derecha o se mantiene en posición según\(D\) sea\(\TMleft\), \(\TMright\), o\(\TMstay\), y el mecanismo entra en estado\(q'\).
Por ejemplo, considere la situación en la Figura\(\PageIndex{1}\).
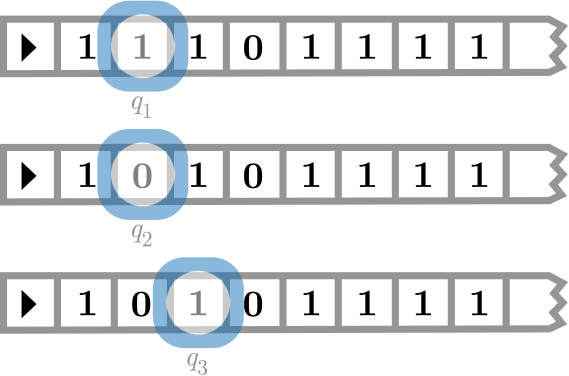
La parte visible de la cinta de la máquina Turing contiene el símbolo de fin de cinta\(\TMendtape\) en el cuadrado más a la izquierda, seguido\(1\) de tres\(0\), a y cuatro\(1\) más.La cabeza lee el tercer cuadrado de la izquierda, que contiene un \(1\), y está en estado\(q_1\) —decimos “la máquina está leyendo un estado\(1\) in”\(q_1\). Si el programa de la máquina Turing regresa, para entrada\(\tuple{q_1, 1}\), el triple\(\tuple{q_2, 0, \TMstay}\), la máquina ahora reemplazaría el\(1\) en el tercer cuadrado con a\(0\), dejaría el cabezal de lectura/escritura donde está, y cambiaría al estado \(q_2\). Si entonces el programa regresa\(\tuple{q_3, 0, \TMright}\) para entrada\(\tuple{q_2, 0}\), la máquina ahora sobrescribiría la\(0\) con otra\(0\) (efectivamente, dejando sin cambios el contenido de la cinta debajo del cabezal de lectura/escritura), movería un cuadrado a la derecha, y entrar al estado\(q_3\). Y así sucesivamente.
Decimos que la máquina se detiene cuando encuentra algún estado,, y símbolo\(q_n\), de\(\sigma\) tal manera que no hay instrucción para\(\tuple{q_n, \sigma}\), es decir, la función de transición para entrada\(\tuple{q_n,\sigma}\) es indefinida. Es decir, la máquina no tiene instrucción para llevar a cabo, y en ese punto, deja de funcionar. La detención a veces está representada por un estado de detención específico\(h\). Esto se demostrará con más detalle más adelante.
La belleza del artículo de Turing, “Sobre números computables”, es que presenta no solo una definición formal, sino también un argumento de que la definición captura la noción intuitiva de computabilidad. A partir de la definición, debe quedar claro que cualquier función computable por una máquina Turing es computable en el sentido intuitivo. Turing ofrece tres tipos de argumento de que lo contrario es cierto, es decir, que cualquier función que naturalmente consideraríamos computable es computable por dicha máquina. Ellos son (en palabras de Turing):
-
Un llamado directo a la intuición.
-
Una prueba de la equivalencia de dos definiciones (en caso de que la nueva definición tenga un mayor atractivo intuitivo).
-
Dando ejemplos de grandes clases de números que son computables.
Nuestro objetivo es tratar de definir la noción de computabilidad “en principio”, es decir, sin tomar en cuenta las limitaciones prácticas de tiempo y espacio. Por supuesto, con la definición más amplia de computabilidad en su lugar, uno puede entonces pasar a considerar el cálculo con recursos acotados; esto forma el corazón del tema conocido como “complejidad computacional”.
Observaciones Históricas
Alan Turing inventó las máquinas Turing en 1936. Si bien su interés en ese momento era la decidabilidad de la lógica de primer orden, el artículo ha sido descrito como un trabajo definitivo sobre los fundamentos del diseño por computadora. En el artículo, Turing se enfoca en números reales computables, es decir, números reales cuyas expansiones decimales son computables; pero señala que no es difícil adaptar sus nociones a funciones computables sobre los números naturales, y así sucesivamente. Observe que esto fue cinco años completos antes de que se construyera la primera computadora de uso general en funcionamiento en 1941 (por el alemán Konrad Zuse en la sala de estar de sus padres), siete años antes de que Turing y sus colegas en Bletchley Park construyeran el Coloso que rompe códigos (1943), nueve años antes del ENIAC estadounidense (1945), doce años antes de que se construyera en Manchester (1948) la primera computadora británica de propósito general, la máquina experimental a pequeña escala de Manchester, y trece años antes de que los estadounidenses probaron por primera vez el BINAC (1949). El Manchester SSEM tiene la distinción de ser la primera computadora de programa almacenado; las máquinas anteriores tenían que ser recableadas a mano para cada nueva tarea.


