11.3.3: La lógica del O

Última actualización
Guardar como PDF

Page ID: 101931

Bradley H. Dowden
California State University Sacramento

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En cualquier declaración de la forma “P o Q” la declaración P se llama “el disjunto izquierdo”, y la Q se llama “el disjunto derecho”. La operación de “o” o “v” se denomina disyunción. Considera la afirmación “x = 5 o y < 19”. Si te dijeran que el disjunto izquierdo o derecho es cierto, pero no lo que es cierto, ¿podrías estar seguro de que el correcto es cierto? No. La moral es la siguiente:

forma de argumento deductivamente inválido de la premisa P o Q luego una barra horizontal y luego una conclusión Q debajo

No obstante, si supieras que el disjunto de izquierda no es cierto, podrías inferir que el correcto es. La forma general es

forma de argumento deductivamente válida de las premisas P o Q y no-P (estas son las dos líneas superiores), luego una barra horizontal, debajo de la cual está la conclusión Q.

Ejercicio\(\PageIndex{1}\)

Declarar si el argumento principal a continuación es una inferencia deductivamente válida, luego describir la forma lógica de la inferencia.

Suponiendo x = 4 e y < 7, como usted ha dicho, entonces x no es desigual a 4.

Responder

Sí, es una inferencia deductivamente válida. Su forma lógica es

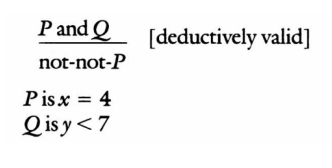
Screen Shot 2019-12-25 a las 4.46.10 PM.png

Ejercicio\(\PageIndex{1}\)

¿Este argumento tiene una forma lógica válida?

Su información establece que el presidente Abraham Lincoln fue asesinado por Ulises Grant. Ahora podemos estar seguros de que John tenía razón cuando dijo: “Abraham Lincoln fue asesinado por Grant o Booth”.

Al tratar de evaluar si el argumento es deductivamente válido, se puede abstraer el argumento principal para producir la siguiente forma:

forma de argumento de tres líneas:
“P”, luego una barra horizontal, luego la conclusión “P o Q”

donde hemos definido

P = El presidente Abraham Lincoln fue asesinado por Ulises Grant.

Q = Abraham Lincoln fue asesinado ya sea por Grant o bien por Booth.

La primera premisa pasa a ser falsa, sin embargo la conclusión es cierta. El problema, sin embargo, no es decidir qué oraciones son verdaderas sino decidir si la forma lógica es deductivamente válida. Lo es.

Responder: Esta es una forma válida. Cualquier argumento con esa forma tiene que ser válido sin importar la frase declarativa por la que sustituya 'P'; y lo mismo ocurre con 'Q'.

Las posibilidades de verdad (y falsedad) para o pueden resumirse en esta tabla de verdad:

una tabla de tres columnas cuyas cabezas de columna son “P” “Q” y “P o Q”. Debajo de esta está la primera fila de valores de verdad T T T. La segunda fila es T F T. La tercera fila es F T T. La cuarta fila final es F F F.