2.4: Diagramas de bloques
- Page ID
- 84145
Un diagrama de bloques es un método gráfico para representar las relaciones entre variables en un sistema. Los símbolos utilizados para formar un diagrama de bloques se introdujeron en la Sección 2.2. Las ventajas de esta representación incluyen el conocimiento del funcionamiento del sistema que a menudo proporciona, su clara indicación de varios bucles de retroalimentación y la simplificación que brinda para determinar las funciones de transferencia que relacionan variables de entrada y salida del sistema. La discusión en esta sección se limita a sistemas lineales, invariantes en el tiempo, con la enumeración de ciertas técnicas útiles para el análisis de sistemas no lineales reservados para el Capítulo 6.
Formando el diagrama de bloques
Así como hay muchos conjuntos completos de ecuaciones que se pueden escribir para describir las relaciones entre variables en un sistema, así hay muchos diagramas de bloques posibles que se pueden usar para representar un sistema en particular. La elección del diagrama de bloques debe hacerse sobre la base de la información que presta a la operación y la facilidad con la que se pueden evaluar las funciones de transferencia requeridas. El siguiente método sistemático es útil para circuitos donde todas las variables de interés son voltajes de nodo.
- Determinar los voltajes de los nodos de interés. El número seleccionado de voltajes no tiene que ser igual al número total de nodos en el circuito, sino que debe ser posible escribir un conjunto completo e independiente de ecuaciones utilizando los voltajes seleccionados. Una línea (que puede dividirse en dos o más ramas en el diagrama de bloques final) representará cada una de estas variables, y estas líneas pueden dibujarse como segmentos aislados.
- Determinar cada una de las tensiones de nodo seleccionadas como una suma ponderada de las otras tensiones seleccionadas y cualquier entrada o perturbación que pueda aplicarse al circuito. Esta determinación requiere un conjunto de ecuaciones de la forma
\[V_j = \sum_{n \ne j} a_{nj} V_n + \sum_m b_{mj} E_m\label{eq2.4.1} \]
donde\(V_k\) está la tensión del nodo\(k\) th y\(E_k\) es la\(k\) th entrada o perturbación. - La variable\(V_j\) se genera como la salida de un punto de suma en el diagrama de bloques. Las entradas al punto de suma provienen de todas las demás variables, entradas y perturbaciones a través de bloques con transmisiones que son los\(a\) 'y' s en\(b\) la Ecuación\(\ref{eq2.4.1}\). Algunos de los bloques pueden tener transmisiones de cero, y estos bloques y las entradas de punto de suma correspondientes pueden eliminarse.
El conjunto de ecuaciones requeridas en el Paso 2 se puede determinar escribiendo ecuaciones de nodo para el circuito completo y resolviendo la ecuación escrita sobre el nodo\(j\) th para\(V_j\) en términos de todas las demás variables. Si no\(V_k\) se requiere cierta tensión de nodo en el diagrama de bloques final, la ecuación relativa\(V_k\) a otras tensiones del sistema se utiliza para eliminar\(V_k\) de todos los demás miembros del conjunto de ecuaciones. Si bien este grado de formalidad suele ser innecesario, siempre produce un diagrama de bloques correcto, y debe usarse si el diagrama deseado no se puede obtener fácilmente por otros métodos.
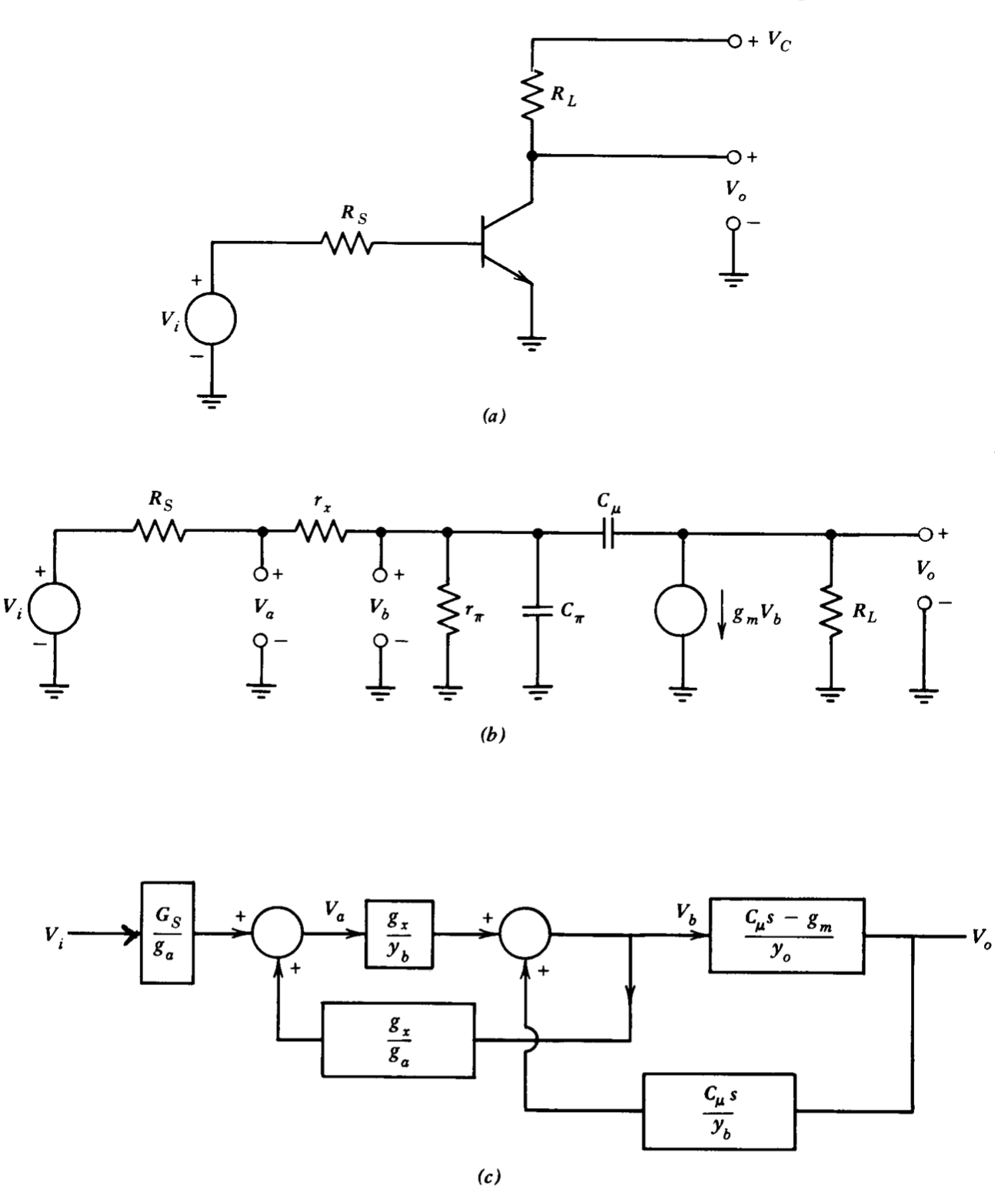
Como ejemplo de construcción de diagrama de bloques por este enfoque formal, considere el amplificador de emisor común que se muestra en la Figura 2.7\(a\). (Los elementos utilizados para el sesgo han sido eliminados por simplicidad). El correspondiente circuito equivalente de señal pequeña se obtiene sustituyendo un híbrido pi (El modelo híbrido-pi se utilizará exclusivamente para el análisis de transistores bipolares que operan en la región lineal. El lector que no está familiarizado con el desarrollo o uso de este modelo se refiere a P. E. Gray y C. L. Searle, Electronic Principles: Physics, Models, and Circuits, Wiley, Nueva York, 1969.) modelo para el transistor y se muestra en la Figura 2.7\(b\). Las ecuaciones de nodo son (G y R (o g y r) se utilizan para identificar las conductancias y resistencias correspondientes, mientras que las Y y Z (o y las y las z) se utilizan para identificar las admisiones e impedancias correspondientes. Así por ejemplo,\(G_A = 1/R_A\) y\(z_b = 1/y_b\).)
\[\begin{array} {rcl} {G_S V_i} & = & {(G_S + g_x) V_a - g_x V_b} \\ {0} & = & {-g_x V_a + [(g_x + g_{\pi}) + (C_{\mu} + C_{\pi} ) s] V_b - C_{\mu} s V_o} \\ {0} & = & {(g_m - C_{\mu} s) V_b + (G_L + C_{\mu} s) V_o} \end{array}\label{eq2.4.2} \]
Si el diagrama de bloques deseado incluye los tres voltajes de nodo, la ecuación\(\ref{eq2.4.2}\) se dispone de manera que cada miembro del conjunto se solucione para la tensión en el nodo sobre el cual se escribió el miembro. Por lo tanto,
\[\begin{array} {rcl} {V_a} & = & {\dfrac{g_x}{g_a} V_b + \dfrac{G_s}{g_a} V_i} \\ {V_b} & = & {\dfrac{g_x}{y_b} V_a + \dfrac{C_{\mu} s}{y_b} V_o} \\ {V_o} & = & {\dfrac{C_{\mu} s - g_m}{y_o} V_b} \end{array} \nonumber \]
donde
\[\begin{array} {rcl} {g_a} & = & {G_S + g_x} \\ {y_b} & = & {[(g_x + g_{\pi}) + (C_{\mu} + C_{\pi}) s]} \\ {y_o} & = & {G_L + C_{\mu} s} \end{array}\nonumber \]
El diagrama de bloques mostrado en la Figura 2.7\(c\) sigue directamente de este conjunto de ecuaciones.
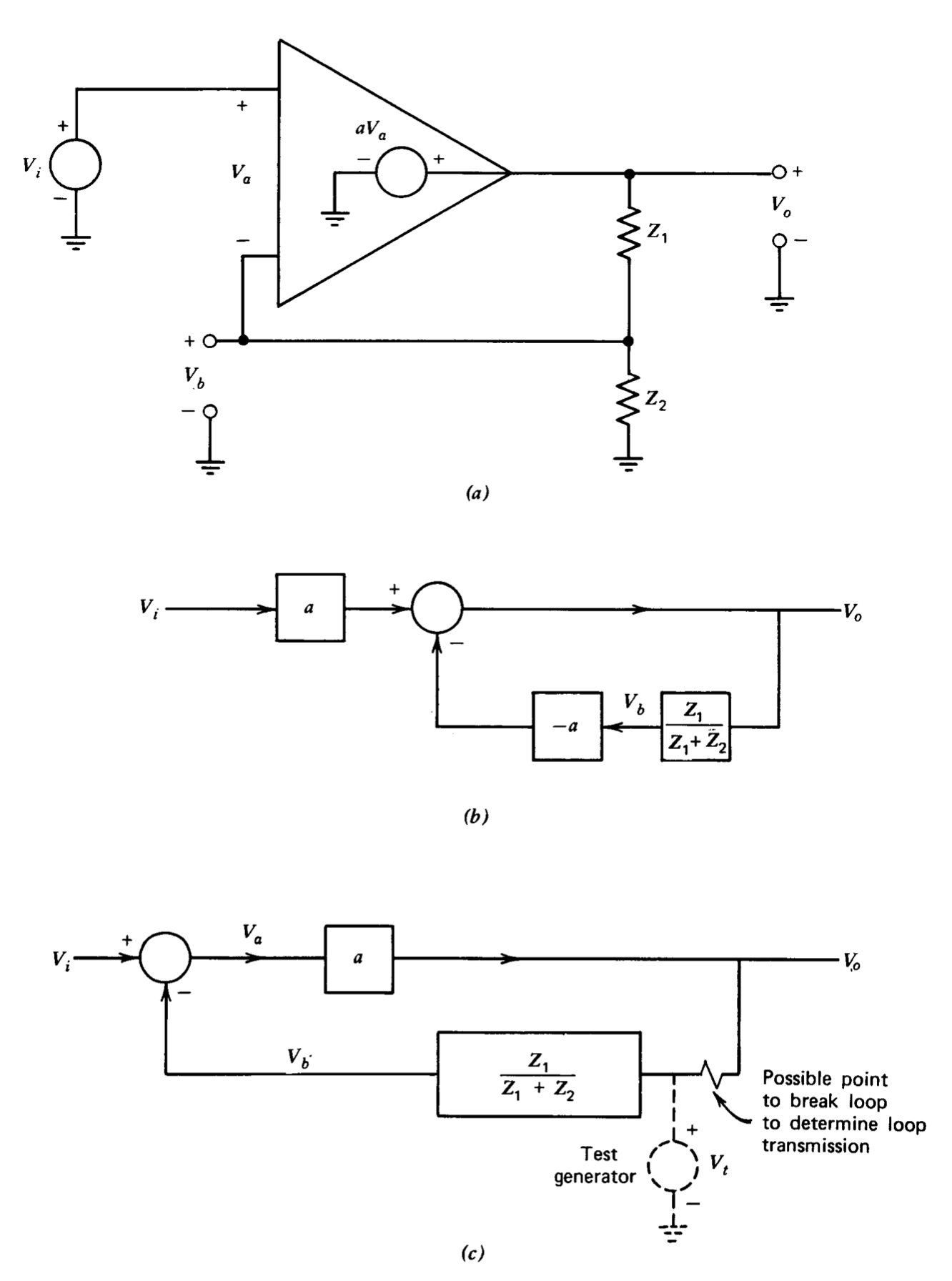
La Figura 2.8 es la base de un ejemplo que es más típico de nuestro uso previsto de diagramas de bloques. Un simple medel de amplificador operacional se muestra conectado como un amplificador no inversor. Se supone que las variables de interés son los voltajes\(V_b\) y\(V_o\). El voltaje\(V_o\) puede relacionarse con el otro voltaje seleccionado,\(V_b\), y el voltaje de entrada\(V_i\),, por superposición.
con\(V_i = 0\),
\[V_o = -a V_b\label{eq2.4.4} \]
mientras que con\(V_b = 0\),
\[V_o = aV_i\label{eq2.4.5} \]
La ecuación relativa\(V_o\) a otros voltajes y entradas seleccionados es simplemente la superposición de las respuestas representadas por Ecuaciones\(\ref{eq2.4.4}\) y\(\ref{eq2.4.5}\), o
\[V_o = aV_i - aV_b\label{eq2.4.6} \]
El voltaje\(V_b\) es independiente\(V_i\) y está relacionado con\(V_o\) como
\[V_b = \dfrac{Z_1}{Z_1 + Z_2} V_o\label{eq2.4.7} \]
Las ecuaciones\(\ref{eq2.4.6}\) y\(\ref{eq2.4.7}\) se combinan fácilmente para formar el diagrama de bloques que se muestra en la Figura 2.8\(b\).
Es posible formar un diagrama de bloques que proporcione una visión algo mayor del funcionamiento del circuito reemplazando Ecuación\(\ref{eq2.4.6}\) por el par de ecuaciones
\[V_a = V_i - V_b\label{eq2.4.8} \]
y
\[V_o = aV_a \label{eq2.4.9} \]
Tenga en cuenta que el conjunto original de ecuaciones no se escribieron incluyendo\(V_a\)\(V_a\), ya que\(V_b\), y\(V_i\) forman un bucle de Kirchhoff y por lo tanto no pueden incluirse todas en un conjunto independiente de ecuaciones.
El diagrama de bloques alternativo que se muestra en la Figura 2.8\(c\) se obtiene de Ecuaciones\(\ref{eq2.4.7}\)\(\ref{eq2.4.8}\),, y\(\ref{eq2.4.9}\). En este diagrama de bloques es claro que el punto sumador modela la función proporcionada por la entrada diferencial del amplificador operacional. Este mismo diagrama de bloques habría evolucionado si V0 y V, se hubieran seleccionado inicialmente como los voltajes del amplificador de interés.
La transmisión de bucle para cualquier sistema representado como diagrama de bloques siempre se puede determinar estableciendo todas las entradas y perturbaciones a cero, rompiendo el diagrama de bloques en cualquier punto dentro del bucle y encontrando la señal devuelta por el bucle en respuesta a una señal de prueba aplicada. Un posible punto para romper el bucle se ilustra en la Figura 2.8c. Con\(V_i = 0\), es evidente que
\[\dfrac{V_o}{V_t} = \dfrac{-aZ_1}{Z_1 + Z_2} \nonumber \]
El mismo resultado se obtiene para la transmisión en bucle si el bucle de la Figura 2.8\(c\) se rompe en otro lugar, o si el bucle de la Figura 2.8\(b\) se rompe en algún punto.
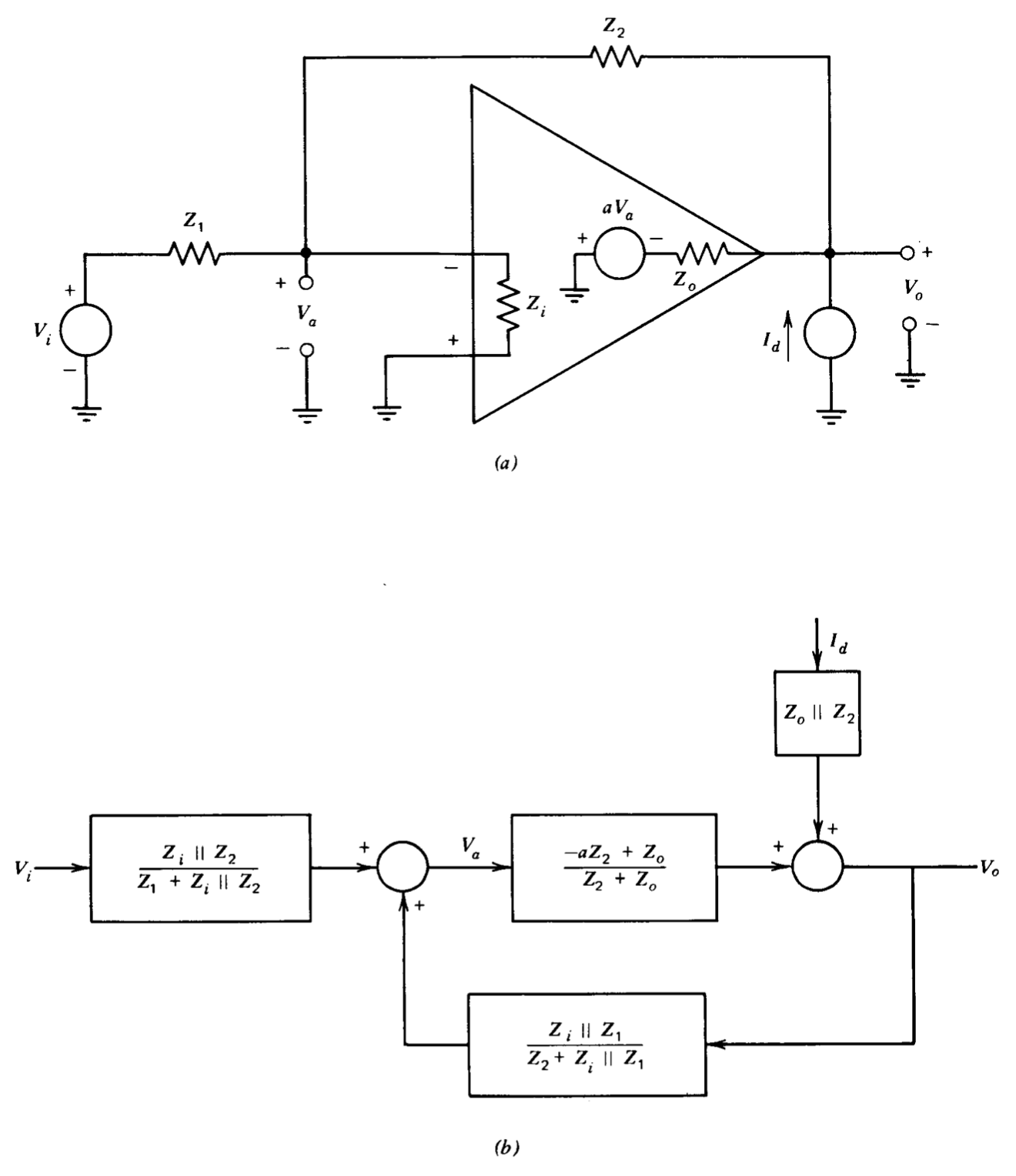
La figura 2.9 es la base de un ejemplo un poco más involucrado. Aquí se muestra un modelo de amplificador operacional bastante detallado, que incluye impedancias de entrada y salida, conectado como un amplificador inversor. Se incluye un generador de corriente perturbadora, y este generador se puede utilizar para determinar la impedancia de salida de bucle cerrado del amplificador\(V_o/I_d\).
Se supone que los voltajes del amplificador de interés son\(V_a\) y\(V_o\). La ecuación relativa\(V_a\) al otro voltaje de interés\(V_o\), la entrada\(V_i\), y la perturbación\(I_d\), se obtiene por superposición (permitiendo que todas las demás señales sean distintas de cero una a la vez y superponiendo resultados) como en el ejemplo anterior. El lector debe verificar los resultados
\[V_a = \dfrac{Z_i || Z_2}{Z_1 + Z_i || Z_2} V_i + \dfrac{Z_i || Z_1}{Z_2 + Z_i || Z_1} V_o \label{eq2.4.11} \]
y
\[V_o = \dfrac{-aZ_2 + Z_o}{Z_2 + Z_o} V_a + (Z_o || Z_2) I_d \label{eq2.4.12} \]
El diagrama de bloques de la Figura 2.9\(b\) sigue directamente de Ecuaciones\(\ref{eq2.4.11}\) y\(\ref{eq2.4.12}\).
Manipulaciones de diagrama de bloques
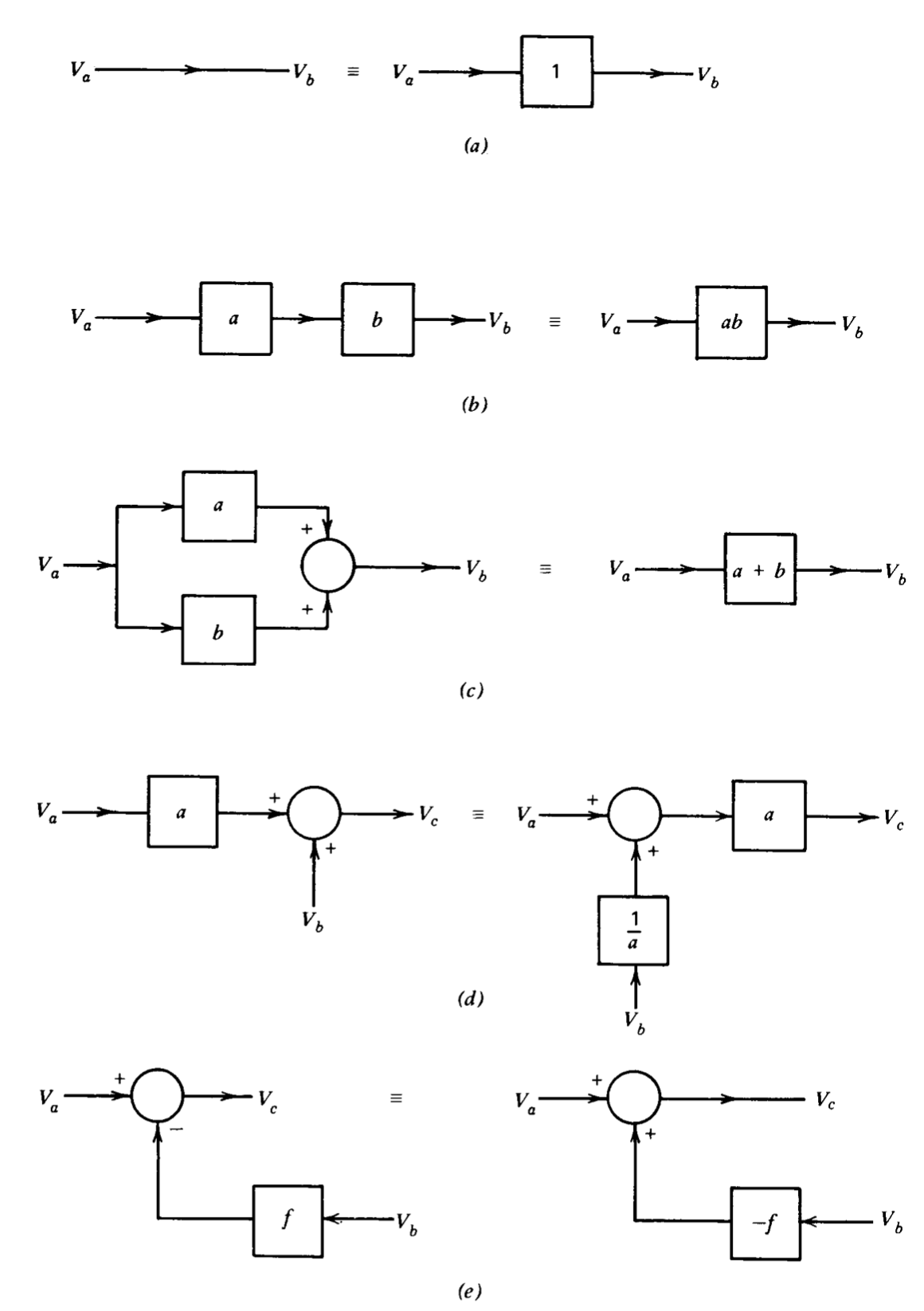
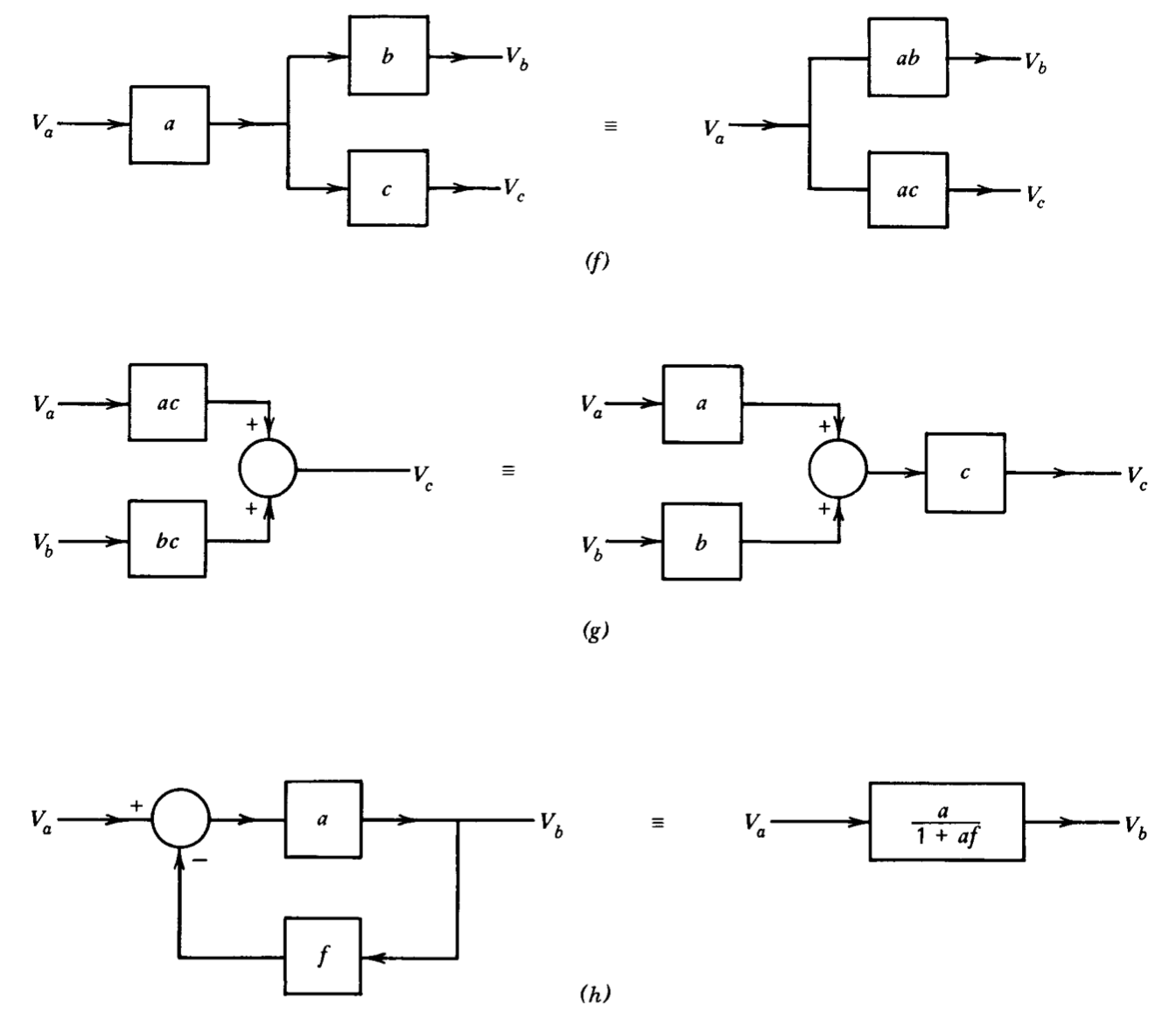
Hay varias formas en que los diagramas de bloques se pueden reestructurar o reordenar mientras se mantiene la expresión de ganancia correcta entre una entrada o perturbación y una salida. Estos diagramas de bloques modificados podrían obtenerse directamente reordenando las ecuaciones utilizadas para formar el diagrama de bloques o usando otras variables del sistema en las ecuaciones. Las equivalencias que se pueden utilizar para modificar diagramas de bloques se muestran en la Figura 2.10.
Es necesario poder encontrar las funciones de transferencia que relacionan salidas a entradas y perturbaciones o las relaciones entre otras variables del sistema a partir del diagrama de bloques del sistema. Estas funciones de transferencia siempre se pueden encontrar aplicando apropiadamente diversas equivalencias de la Figura 2.10 hasta obtener un sistema de bucle único. La función de transferencia puede entonces ser determinada por reducción de bucle (Figura 2.10\(h\)). Alternativamente, una vez que el diagrama de bloques se ha reducido a un solo bucle, las cantidades importantes del sistema son evidentes. Tanto la transmisión en bucle como la ganancia de bucle cerrado que se aproxima para una magnitud de transmisión de bucle grande se pueden encontrar por inspección.
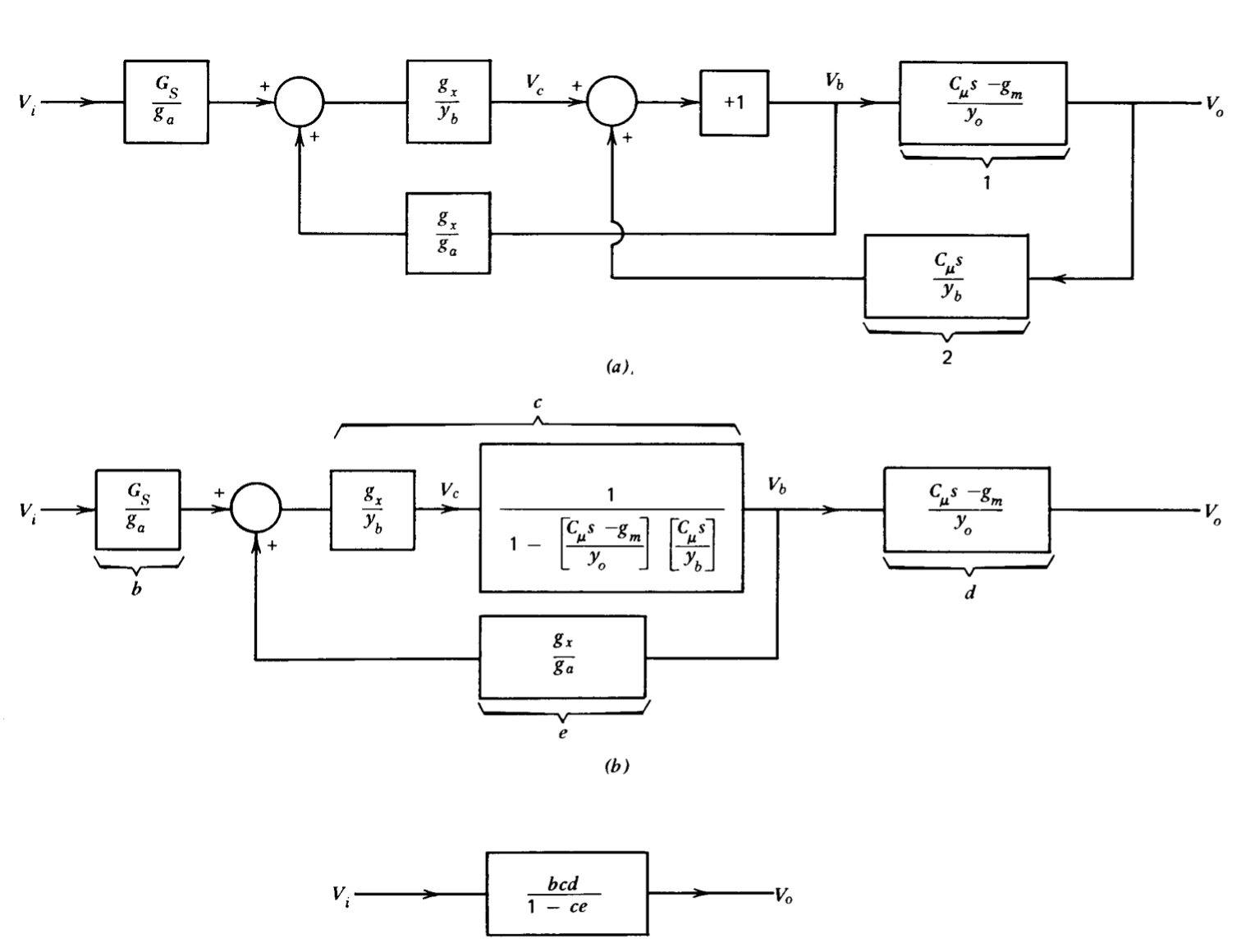
La Figura 2.11 ilustra el uso de equivalencias para reducir el diagrama de bloques del amplificador de emisor común previamente mostrado como Figura 2.7\(c\). La Figura 2.11\(a\) es idéntica a la Figura 2.7\(c\), con las excepciones de que una línea ha sido reemplazada por un bloque de unidad-ganancia (ver Figura 2. 10\(a\)) y se\(V_c\) ha definido una variable intermedia. Estos cambios aclaran la transformación de la Figura 2.11\(a\) a 2.11\(b\), la cual se realiza de la siguiente manera. La función de transferencia de\(V_c\) a\(V_b\) se determina utilizando la equivalencia de la Figura 2.10\(h\), reconociendo que la ruta de retroalimentación para este bucle es producto de las funciones de transferencia de los bloques 1 y 2. La función de transferencia\(V_b/ V_c\) se incluye en el bucle restante, y la función de transferencia del bloque 1 enlaza\(V_o\) con\(V_b\).
Las equivalencias de las figuras 2.10\(b\) y 2.10\(h\) utilizando la identificación de funciones de transferencia mostradas en la figura 2.11b (desafortunadamente, a medida que se reduce un diagrama, las complejidades de las funciones de transferencia de los bloques residuales aumentan) se utilizan para determinar la función de transferencia general indicada en Figura 2.11\(c\).
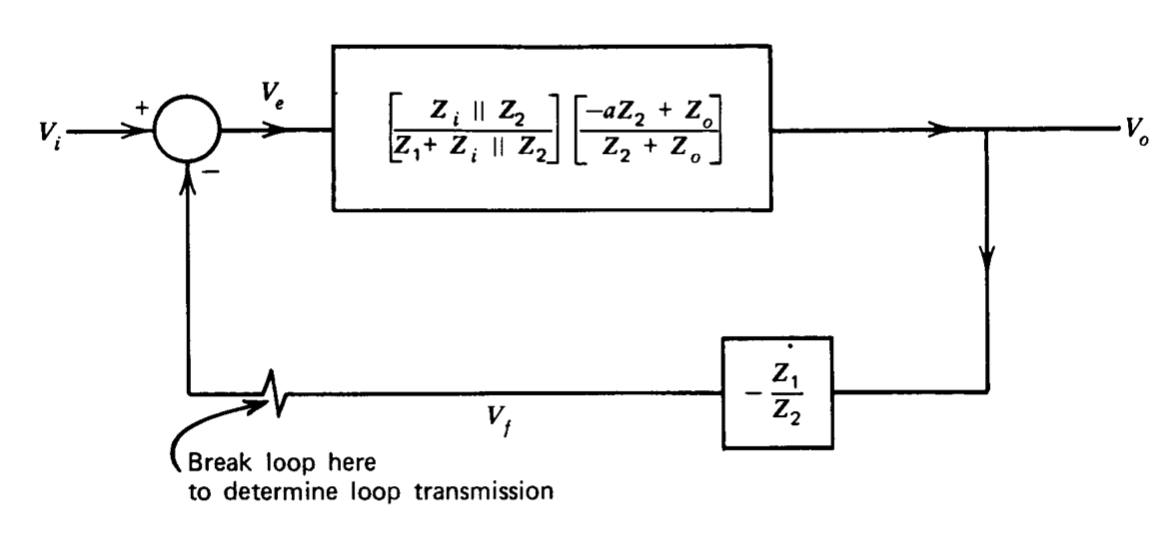
La conexión de amplificador inversor (Figura 2.9) se utiliza como otro ejemplo de reducción de diagrama de bloques. La función de transferencia\(V_o\) relacionada\(V_i\) en la Figura 2.9 se\(b\) puede reducir a la forma de bucle único absorbiendo el bloque de la izquierda en este diagrama (equivalencia en la Figura 2.10\(d\)). La Figura 2.12 muestra el resultado de esta absorción después de simplificar algebraicamente la trayectoria de retroalimentación, eliminar la entrada perturbadora, y usar la equivalencia de la Figura 2.10\(e\) para introducir una inversión en el punto de suma. La ganancia de este sistema se aproxima al recíproco de la trayectoria de retroalimentación para una transmisión de bucle grande; por lo tanto, la ganancia de bucle cerrado ideal es
\[\dfrac{V_o}{V_i} = -\dfrac{Z_2}{Z_1} \nonumber \]
La ganancia hacia adelante para este sistema es
\[\begin{array} {rcl} {\dfrac{V_o}{V_e}} & = & {\left [\dfrac{Z_i || Z_2}{Z_1 + Z_i || Z_2} \right ] \left [\dfrac{-aZ_2 + Z_o}{Z_2 + Z_o} \right ] } \\ {} & = & {\left [\dfrac{Z_i || Z_2}{Z_1 + Z_i || Z_2} \right ] \left [\dfrac{-aZ_2}{Z_2 + Z_o} \right ] + \left [\dfrac{Z_i || Z_2}{Z1 + Z_i || Z_2} \right ] \left [\dfrac{Z_o}{Z_2 + Z_o} \right ] } \end{array}\label{eq2.4.14} \]
El término final en el lado derecho de la ecuación\(\ref{eq2.4.14}\) refleja el hecho de que alguna fracción de la señal de entrada se acopla directamente a la salida a través de la red de retroalimentación, incluso si la ganancia de voltaje del amplificador\(a\) es cero. Dado que las impedancias incluidas en este término son generalmente resistivas o capacitivas, la magnitud de este término de acoplamiento será menor que una en todas las frecuencias. Del mismo modo, el componente de transmisión de bucle atribuible a esta trayectoria directa, determinado por establecer\(a = 0\) y abrir el bucle es
\[\begin{array} {rcl} {\dfrac{V_f}{V_e} |_{a = 0}} & = & {\left [\dfrac{Z_1}{Z_2} \right ] \left [\dfrac{Z_i || Z_2}{Z_1 + Z_i || Z_2} \right ] \left [\dfrac{Z_o}{Z_2 + Z_o} \right ]} \\ {} & = & {\left [\dfrac{Z_i Z_1}{Z_i Z_1 + Z_i Z_2 + Z_1 Z_2} \right ] \left [\dfrac{Z_o}{Z_2 + Z_o} \right ]} \end{array}\label{eq2.4.15} \]
y será menor de uno en magnitud en todas las frecuencias cuando las impedancias involucradas sean resistivas o capacitivas.
Si la magnitud de transmisión de bucle de la conexión operacional-amplificador es grande en comparación con una, el componente atribuible al acoplamiento directo a través de la red de retroalimentación (Ecuación\(\ref{eq2.4.15}\)) debe ser insignificante. En consecuencia, la ganancia de trayectoria de avance del sistema se puede aproximar como
\[\dfrac{V_o}{V_e} \simeq \left [\dfrac{-aZ_2}{Z_2 + Z_o} \right ] \left [\dfrac{Z_i || Z_2}{Z_1 + Z_i || Z_2} \right ] \nonumber \]
en este caso. La transmisión de bucle correspondiente se convierte en
\[\dfrac{V_f}{V_e} \simeq \left [\dfrac{-aZ_1}{Z_2 + Z_o} \right ] \left [\dfrac{Z_i || Z_2}{Z_1 + Z_i || Z_2} \right ] \nonumber \]
Con frecuencia se encuentra que el término de transmisión en bucle que implica el acoplamiento directo a través de la red de retroalimentación puede descuidarse en conexiones prácticas de amplificador operacional, reflejando la hipótesis razonable de que el mecanismo de ganancia dominante es el amplificador en lugar de la red pasiva. Si bien esta aproximación normalmente produce excelentes resultados en frecuencias donde la ganancia del amplificador es grande, existen sistemas donde los cálculos de estabilidad son incorrectos cuando se usa la aproximación. La razón es que la estabilidad depende en gran medida del comportamiento de la transmisión en bucle a frecuencias donde su magnitud es cercana a una, y la ganancia del amplificador puede no dominar en estas frecuencias.
Ganancia de bucle cerrado
Siempre es posible determinar la ganancia que relaciona cualquier señal en un diagrama de bloques con una entrada o una perturbación manipulando el diagrama de bloques hasta que una sola ruta conecte las dos cantidades de interés. Alternativamente, es posible utilizar un método desarrollado por Mason (S. J. Mason y H. J. Zimmermann, Electronic Circuits, Signals, and Systems, Wiley, Nueva York, 1960, Capítulo 4, “Linear Signal-Flow Grafs.”) para calcular ganancias directamente a partir de un diagrama de bloques no reducido.
Para determinar la ganancia entre una entrada o perturbación y cualquier otro punto del diagrama, es necesario identificar dos características topológicas de un diagrama de bloques. Un camino es una sucesión continua de bloques, líneas y puntos de suma que conectan la entrada y la señal de interés y a lo largo de los cuales no se encuentra ningún elemento más de una vez. Las líneas pueden ser atravesadas solo en la dirección del flujo de información (con la flecha). Es posible en general tener más de una ruta conectando una entrada a una salida u otra señal de interés. La ganancia de camino es producto de las ganancias de todos los elementos en un camino. Un bucle es una sucesión cerrada de bloques, líneas y
puntos de suma atravesados con las flechas, a lo largo de los cuales no se encuentra ningún elemento más de una vez por ciclo. La ganancia de bucle es el producto de las ganancias de todos los elementos en un bucle. Es necesario incluir las inversiones indicadas por signos negativos en los puntos de suma al calcular las ganancias de trayectoria o bucle. La expresión general para la ganancia o transmisión de un diagrama de bloques es
\[T = \dfrac{\displaystyle \sum_a P_a \left(1 - \displaystyle \sum_b L_b + \displaystyle \sum_{c,d} L_c L_d - \displaystyle \sum_{e,f,g} L_e L_f L_g + \cdots -\right)}{1 - \displaystyle \sum_h L_h + \sum_{i, j} L_i L_j - \displaystyle \sum_{k, l, m} L_k L_l L_m + \cdots -} \label{eq2.4.18} \]
El numerador de la expresión de ganancia es la suma de las ganancias de todos los caminos que conectan la entrada y la señal de interés, con cada ganancia de ruta escalada por un cofactor. La primera suma en un cofactor incluye las ganancias de todos los bucles que no tocan (comparten un bloque común o punto de suma con) la ruta; la segunda suma incluye todos los productos posibles de ganancias de bucle para bucles que no tocan la ruta o entre sí tomados dos a la vez; la tercera suma incluye todos los triples posibles productos de ganancias de bucle para bucles que no tocan el camino ni entre sí; etc.
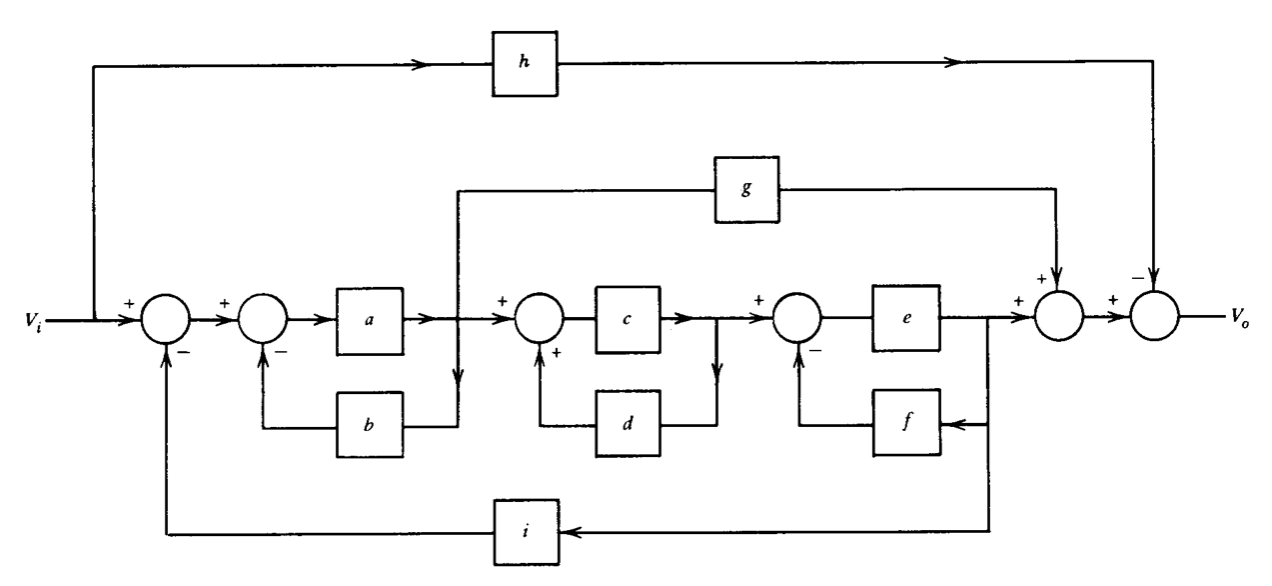
El denominador de la expresión de ganancia se denomina ecuación determinante o característica del diagrama de bloques, y es idénticamente igual a uno menos la transmisión en bucle del diagrama de bloques completo. La primera suma en la ecuación característica incluye todas las ganancias de bucle; la segunda todos los productos posibles de las ganancias de bucles no tocados tomados dos a la vez; etc. Dos ejemplos servirán para aclarar la evaluación de la expresión de ganancia. La Figura 2.13 proporciona el primer ejemplo. Para aplicar la fórmula de ganancia de Mason para la transmisión\(V_o/ V_i\), se identifican los caminos y bucles y
se evalúan sus ganancias. Los resultados son:
\[\begin{array} {rcl} {P_1} & = & {ace} \\ {P_2} & = & {ag} \\ {P_3} & = & {-h} \\ {L_1} & = & {-ab} \\ {L_2} & = & {cd} \\ {L_3} & = & {-ef} \\ {L_4} & = & {-acei} \end{array}\nonumber \]
La topología de la Figura 2.13 muestra que path\(P_1\) comparte bloques comunes con y por lo tanto toca todos los bucles. \(P_2\)La ruta no toca los bucles\(L_2\) o\(L_3\), mientras que la ruta\(P_3\) no toca ningún bucle. Del mismo modo\(L_1\), los bucles\(L_2\),, y\(L_3\) no se tocan entre sí, sino todos tocan el bucle\(L_4\). La ecuación\(\ref{eq2.4.18}\) evaluada para este sistema se convierte en
\[\dfrac{V_o}{V_i} = \dfrac{P_1 + P_2 (1 - L_2 - L_3 + L_2 L_3) + P_3 (1 - L_1 - L_2 - L_3 - L_4 + L_1 L_2 + L_2 L_3 + L_1 L_3 - L_1 L_2 L_3)}{1 - L_1 - L_2 - L_3 - L_4 + L_1 L_2 + L_2 L_3 + L_1 L_3 - L_1 L_2 L_3} \nonumber \]
Un segundo ejemplo de reducción de diagrama de bloques y algún refuerzo de las técnicas utilizadas para describir un sistema en forma de diagrama de bloques es proporcionado por el conjunto de ecuaciones algebraicas
\[\begin{array} {rcl} {X + Y + Z} & = & {6} \\ {X + Y - Z} & = & {0} \\ {2X + 3Y + Z} & = & {11} \end{array}\label{eq2.4.20} \]
Para representar este conjunto de ecuaciones en forma de diagrama de bloques, se reescriben las tres ecuaciones
\[\begin{array} {rcl} {X} & = & {-Y - Z + 6} \\ {Y} & = & {-X + Z} \\ {Z} & = & {-2X - 3Y + 11} \end{array} \nonumber \]
Este conjunto de ecuaciones se muestra en forma de diagrama de bloques en la Figura 2.14. Si usamos la identificación de bucles en esta figura, las ganancias de bucle son
\[\begin{array} {rcl} {L_1} & = & {1} \\ {L_2} & = & {-3} \\ {L_3} & = & {-3} \\ {L_4} & = & {2} \\ {L_5} & = & {2} \end{array} \nonumber \]
Como todos los bucles tocan, el determinante de cualquier expresión de ganancia para este sistema es
\[1 - L_1 - L_2 - L_3 - L_4 - L_5 = 2 \nonumber \]
(Este valor es, por supuesto, idénticamente igual al determinante de los coeficientes de la Ecuación\(\ref{eq2.4.20}\).)
Supongamos que\(X\) se requiere el valor de. El diagrama de bloques muestra una ruta con una transmisión de +1 conectando la excitación con un valor de 6 a\(X\). Este camino no toca\(L_2\). También hay dos caminos (aproximadamente paralelos\(L_3\) y\(L_5\)) con transmisiones de - 1 conectando la excitación con un valor de 11 a\(X\). Estos caminos tocan todos los bucles. La linealidad nos permite combinar las\(X\) respuestas relacionadas con las dos excitaciones, con el resultado de que
\[X = \dfrac{6[1 - (-3)] - 11 -11}{2} = 1 \nonumber \]
El lector debe verificar que este método arroja los valores\(Y = 2\) y\(Z = 3\) para las otras dos variables dependientes.


