2.3: Ventajas de la retroalimentación
- Page ID
- 84144
Existe una tendencia frecuente por parte de los no iniciados a asociar propiedades casi mágicas a la retroalimentación. Un examen más detallado muestra que muchos beneficios asumidos de la retroalimentación son ilusorios. La principal ventaja es que la retroalimentación nos permite reducir la sensibilidad de un sistema a los cambios en la ganancia de ciertos elementos. Esta reducción en la sensibilidad se obtiene sólo a cambio de un incremento en la magnitud de la ganancia de uno o más de los elementos en el sistema.
En algunos casos también es posible reducir los efectos de las perturbaciones aplicadas al sistema. Veremos que esta moderación siempre se puede lograr, al menos conceptualmente, sin retroalimentación, aunque el enfoque de retroalimentación suele ser una solución más práctica. Las limitaciones de esta técnica impiden la reducción de cantidades tales como ruido o deriva en la entrada de un amplificador; por lo tanto, la retroalimentación no proporciona un método para detectar señales que no pueden ser detectadas por otros medios.
La retroalimentación proporciona un método conveniente para modificar la impedancia de entrada y salida de los amplificadores, aunque al igual que con la reducción de perturbaciones, es al menos conceptualmente posible obtener resultados similares sin retroalimentación.
Efecto de la retroalimentación sobre los cambios en la ganancia de bucle abierto
Como se mencionó anteriormente, la principal ventaja de los sistemas de retroalimentación en comparación con los sistemas de bucle abierto es que la retroalimentación proporciona un método para reducir la sensibilidad del sistema a los cambios en la ganancia de ciertos elementos. Esta ventaja se puede ilustrar usando el diagrama de bloques de la Figura 2.2. Si se supone que la perturbación es cero, la ganancia de bucle cerrado para el sistema es
\[\dfrac{V_o}{V_i} = \dfrac{a}{1 + af} \triangleq A \nonumber \]
(Con frecuencia usaremos la letra mayúscula\(A\) para denotar ganancia de bucle cerrado, mientras que la a minúscula normalmente se reserva para una ganancia de ruta directa).
La cantidad af es la negativa de la transmisión en bucle para este sistema. La transmisión de bucle se determina estableciendo todas las entradas externas (y dis-turbances) a cero, rompiendo el sistema en cualquier punto dentro del bucle y determinando la relación de la señal devuelta por el sistema a una entrada de prueba aplicada. (Un ejemplo de este tipo de cálculo se da en la Sección 2.4.1.) Si el sistema es un sistema de retroalimentación negativa, la transmisión en bucle es negativa. El signo negativo en la entrada del punto sumador que se incluye en el bucle mostrado en la Figura 2.2 indica que la retroalimentación es negativa para este sistema si\(a\) y\(f\) tienen el mismo signo. Alternativamente, la inversión necesaria para la retroalimentación negativa podría ser suministrada por el amplificador o el elemento de retroalimentación.
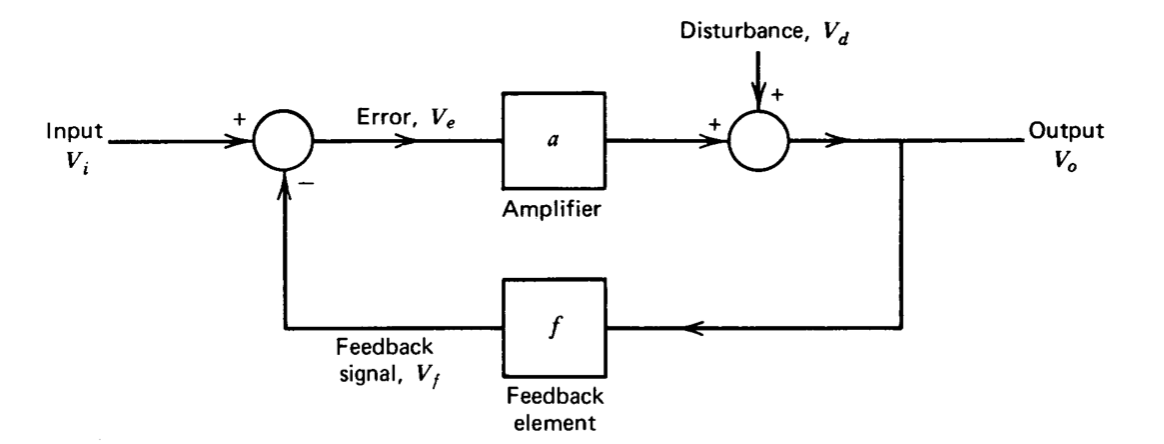
La ecuación 2.2 muestra que la retroalimentación negativa disminuye la magnitud de la ganancia de un amplificador ya que a medida que\(f\) se incrementa desde cero, la magnitud de la ganancia de bucle cerrado disminuye si\(a\) y\(f\) tienen este mismo signo. El resultado es general y se puede utilizar como prueba de retroalimentación negativa.
También es posible diseñar sistemas con retroalimentación positiva. Dichos sistemas no son tan útiles para nuestros fines y no se consideran en detalle.
La expresión de ganancia de bucle cerrado muestra que a medida que la magnitud de transmisión de bucle se vuelve grande en comparación con la unidad, la ganancia de bucle cerrado se acerca al valor\(1/f\). El significado de esta relación es el siguiente. El amplificador normalmente incluirá elementos activos cuyas características varían en función de la edad y las condiciones de funcionamiento. Esta incertidumbre puede ser inevitable ya que los elementos activos no están disponibles con la estabilidad requerida para una aplicación determinada, o bien puede introducirse como un compromiso a cambio de ventajas económicas o de otro tipo.
Por el contrario, la red de retroalimentación normalmente atenúa las señales y, por lo tanto, puede construirse frecuentemente usando solo componentes pasivos. Afortunadamente, los componentes pasivos con valores estables y conocidos con precisión están fácilmente disponibles. Si la magnitud de la transmisión en bucle es suficientemente alta, la ganancia de bucle cerrado se vuelve dependiente principalmente de las características de la red de retroalimentación.
Esta característica se puede enfatizar calculando el cambio fraccionario en la ganancia de bucle cerrado\(d(V_o/V_i)/(V_o/V_i)\) causado por un cambio fraccionario dado en la ganancia de ruta directa del amplificador\(da/a\), con el resultado
\[\dfrac{d(V_o/V_i)}{(V_o/V_i)} = \dfrac{da}{a} \left (\dfrac{1}{1 + af} \right ) \nonumber \]
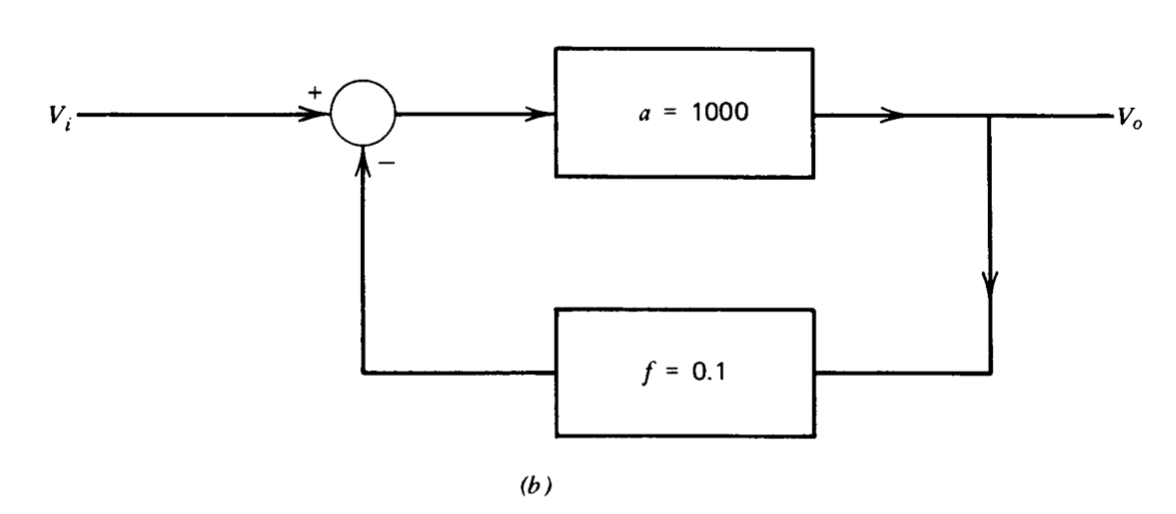
La ecuación 2.3 muestra que los cambios en la magnitud de a pueden atenuarse a niveles insignificantes si\(af\) es suficientemente grande. La cantidad\(1 + af\) que relaciona los cambios en la ganancia de trayectoria directa con los cambios en la ganancia de bucle cerrado se denomina frecuentemente la desensitividad de un sistema de retroalimentación. La Figura 2.3 ilustra este proceso de desensibilización comparando dos conexiones de amplificador en tendido a dar una ganancia de entrada/salida de 10. Claramente, la ganancia de entrada-salida es idéntica a a en la Figura 2.3 y\(a\), por lo tanto, tiene el mismo cambio fraccional en la ganancia que a. Las ecuaciones 2.2 y 2.3 muestran que la ganancia de bucle cerrado para el sistema de la Figura 2.3\(b\) es aproximadamente 9.9, y que el cambio fraccional en la ganancia de bucle cerrado es menor del 1% .del cambio fraccionario en la ganancia de ruta hacia adelante de este sistema.
La característica de desensitividad del proceso de retroalimentación se obtiene únicamente a cambio de ganancia excesiva proporcionada en el sistema. Volviendo al ejemplo que involucra la Figura 2.2, vemos que la ganancia de bucle cerrado para el sistema es\(a/(1 + af)\), mientras que la ganancia de trayectoria directa proporcionada por el amplificador es\(a\). La desensitividad es idéntica a la relación entre la ganancia de trayectoria directa y la ganancia de bucle cerrado. Las conexiones de retroalimentación son únicas en su capacidad para intercambiar automáticamente el exceso de ganancia por desensitividad.
Es importante subrayar el hecho de que los cambios en la ganancia del elemento de retroalimentación tienen influencia directa en la ganancia de bucle cerrado del sistema, por lo que concluimos que es necesario observar o medir la variable de salida de un sistema de retroalimentación con precisión para realizar las ventajas de retroalimentación.
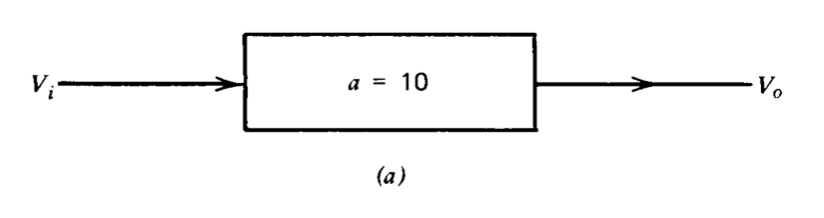
Efecto de la retroalimentación sobre las no linealidades
Debido a que la retroalimentación reduce la sensibilidad de un sistema a los cambios en la ganancia de bucle abierto, a menudo puede moderar los efectos de las no linealidades. La Figura 2.4 ilustra este proceso. El camino directo en esta conexión consiste en un amplificador con una ganancia de 1000 seguido de un elemento no lineal que podría ser una representación idealizada de las características de transferencia de una etapa de salida de potencia. Las características de transferencia del elemento no lineal muestran estas cuatro regiones distintas:
- Una zona inactiva, donde la salida permanece cero hasta que la magnitud de entrada supera 1 voltio. Esta región modela la distorsión de cruce asociada con muchos tipos de amplificadores de potencia.
- Una región lineal, donde la ganancia incremental del elemento es uno.
- Una región de limitación suave, donde la ganancia incremental del elemento se baja a 0.1.
- Una región de limitación dura o saturación donde la ganancia incremental del elemento es cero.
El rendimiento del sistema se puede determinar reconociendo que, dado que el elemento no lineal es lineal por tramos, todas las relaciones de transferencia deben ser lineales por tramos. Los valores de todas las variables en un punto de interrupción se pueden encontrar mediante un proceso iterativo. Supongamos, por ejemplo, que las variables asociadas al elemento no lineal son tales que este elemento se encuentra en su punto de interrupción conectando una pendiente de cero a una pendiente de +1. Esta condición solo ocurre para\(v_A = 1\) y\(v_B = 0\). Si\(v_B = v_O = 0\), la señal\(v_F\) debe ser cero, ya que\(v_F = 0.1 v_O\). De igual manera, con\(v_A = 1, v_E = 10^{-3} v_A = 10^{-3}\). Ya que las relaciones en el punto de suma implican\(v_E = v_I - v_F\), o\(v_I = v_E + v_F\),\(v_I\) deben ser iguales\(10^{-3}\). Los valores de las variables en todos los demás puntos de interrupción se pueden encontrar por razonamiento similar. Los resultados se resumen en la Tabla 2.1.
| \(v_I\) | \(v_E = v_I - v_F\) | \(v_A = 10^3 v_E\) | \(v_B = v_O\) | \(v_F = 0.1 v_O\) |
|---|---|---|---|---|
| \ (V_i\) "><-0.258 | \ (v_e = v_i - v_f\) ">\(v_I + 0.250\) | \ (V_a = 10^3 v_E\) ">\(10^3 v_I + 250\) | \ (V_b = V_o\) ">-2.5 | \ (V_f = 0.1 V_o\) ">-0.25 |
| \ (V_i\) ">-0.258 | \ (V_e = V_i - V_f\) ">-0.008 | \ (V_a = 10^3 v_E\) ">-8 | \ (V_b = V_o\) ">-2.5 | \ (V_f = 0.1 V_o\) ">-0.25 |
| \ (V_i\) ">-0.203 | \ (V_e = V_i - V_f\) ">-0.003 | \ (V_a = 10^3 v_E\) ">-3 | \ (V_b = V_o\) ">-2 | \ (V_f = 0.1 V_o\) ">-0.2 |
| \ (V_i\) ">\(-10^{-3}\) | \ (v_e = v_i - v_f\) ">\(-10^{-3}\) | \ (V_a = 10^3 v_E\) ">-1 | \ (V_b = V_o\) ">0 | \ (V_f = 0.1 V_o\) ">0 |
| \ (V_i\) ">\(10^{-3}\) | \ (v_e = v_i - v_f\) ">\(10^{-3}\) | \ (V_a = 10^3 v_E\) ">1 | \ (V_b = V_o\) ">0 | \ (V_f = 0.1 V_o\) ">0 |
| \ (V_i\) ">0.203 | \ (V_e = V_i - V_f\) ">0.003 | \ (V_a = 10^3 v_E\) ">3 | \ (V_b = V_o\) ">2 | \ (V_f = 0.1 V_o\) ">0.2 |
| \ (V_i\) ">0.258 | \ (V_e = V_i - V_f\) ">0.008 | \ (V_a = 10^3 v_E\) ">8 | \ (V_b = V_o\) ">2.5 | \ (V_f = 0.1 V_o\) ">0.25 |
| \ (V_i\) ">>0.258 | \ (v_e = v_i - v_f\) ">\(v_I - 0.250\) | \ (V_a = 10^3 v_E\) ">\(10^3 v_I - 250\) | \ (V_b = V_o\) ">2.5 | \ (V_f = 0.1 V_o\) ">0.25 |
La relación de transferencia entrada-salida para el sistema mostrado en la Figura 2.4\(c\) se genera a partir de los valores incluidos en la Tabla 2.1. La relación de transferencia también se puede encontrar usando la ganancia incremental hacia adelante, o 1000 veces la ganancia incremental del elemento no lineal, como el valor para\(a\) en la Ecuación 2.2. Si la magnitud de la señal\(v_A\) es inferior a 1 voltio, a es cero y la ganancia incremental de bucle cerrado del sistema también es cero. Si\(v_A\) está entre 1 y 3 voltios, a es\(10^3\), por lo que la ganancia incremental de bucle cerrado es 9.9. Del mismo modo, la ganancia incre mental de bucle cerrado es de 9.1 para\(3 < v_A < 8\).
Observe en la Figura 2.4\(c\) que la retroalimentación reduce drásticamente el ancho de la zona muerta y el cambio en la ganancia a medida que los límites suaves de la etapa de salida. Una vez que el amplificador se satura, la transmisión de bucle incremental se vuelve cero, y como resultado la retroalimentación no puede mejorar el rendimiento en esta región.
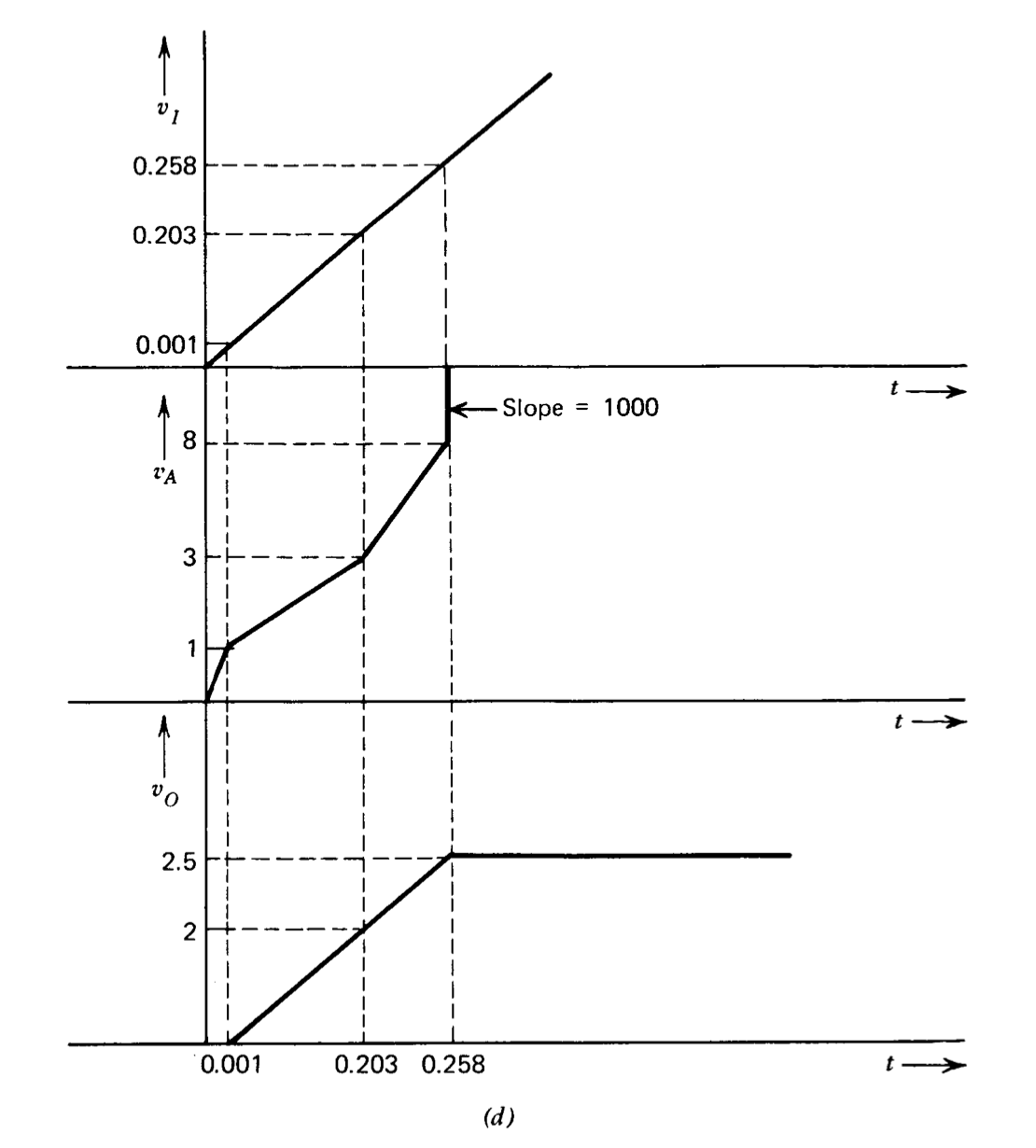
La Figura 2.4\(d\) proporciona información sobre el funcionamiento del circuito al comparar la salida del sistema y el voltaje\(v_A\) para una entrada de rampa de unidad. La salida sigue siendo una buena aproximación a la entrada hasta que se alcanza la saturación. La señal en el elemento no lineal es “predistorsionada” por retroalimentación de tal manera que fuerza la salida de este elemento a ser casi lineal.
La técnica de emplear retroalimentación para reducir los efectos de los elementos no lineales en el rendimiento del sistema es un método potente y ampliamente utilizado que evoluciona directamente de la desensitividad para obtener cambios proporcionados por la retroalimentación. En algunas aplicaciones, la retroalimentación se utiliza para contrarrestar las inevitables no linealidades asociadas con los elementos activos. En otras aplicaciones, la retroalimentación se utiliza para mantener el rendimiento cuando las no linealidades resultan de compromisos económicos. Considera el amplificador de potencia que proporcionó la motivación para el ejemplo anterior. Los diseños para las etapas lineales de manejo de potencia son complejos y costosos debido a que se debe incluir la compensación de los voltajes de base a emisor de los transistores y variaciones de ganancia con punto de operación. Normalmente se obtienen ventajas económicas si se reduce la linealidad de la etapa de manejo de energía y se agregan etapas de ganancia de voltaje de baja potencia (posiblemente en forma de amplificador operativo) antes de la etapa de salida para que la retroalimentación pueda usarse para restaurar la linealidad del sistema.
Si bien esta sección ha destacado el uso de retroalimentación para reducir los efectos de las no linealidades asociadas con el elemento de ganancia hacia adelante de un sistema, la retroalimentación también se puede utilizar para producir no linealidades con características bien controladas. Si el elemento de retroalimentación en un sistema con transmisión de bucle grande es no lineal, la salida del sistema se vuelve aproximadamente\(v_O = f^{-1} (v_I)\). Aquí\(f^{-1}\) está la inversa de la relación de transferencia de elementos de retroalimentación, en el sentido de que\(f^{-1} [f(V)] = V\). Por ejemplo, se pueden usar transistores o diodos con características exponenciales como elementos de retroalimentación alrededor de un amplificador operacional para proporcionar una relación de transferencia logarítmica de bucle cerrado.
Alteraciones en sistemas de retroalimentación
La retroalimentación proporciona un método para reducir la sensibilidad de un sistema a ciertos tipos de perturbaciones. Esta ventaja se ilustra en la Figura 2.5. A este sistema se aplican tres fuentes diferentes de perturbaciones. La perturbación\(V_{d1}\) ingresa al sistema en el mismo punto que la entrada del sistema, y podría representar el ruido asociado con la etapa de entrada de un amplificador. La perturbación\(V_{d2}\) ingresa al sistema en un punto intermedio, y podría representar una perturbación del zumbido asociado con el voltaje mal filtrado que a menudo se usa para alimentar una etapa de salida de amplificador. La perturbación\(V_{d3}\) entra en la salida del amplificador y podría representar características de carga cambiantes.
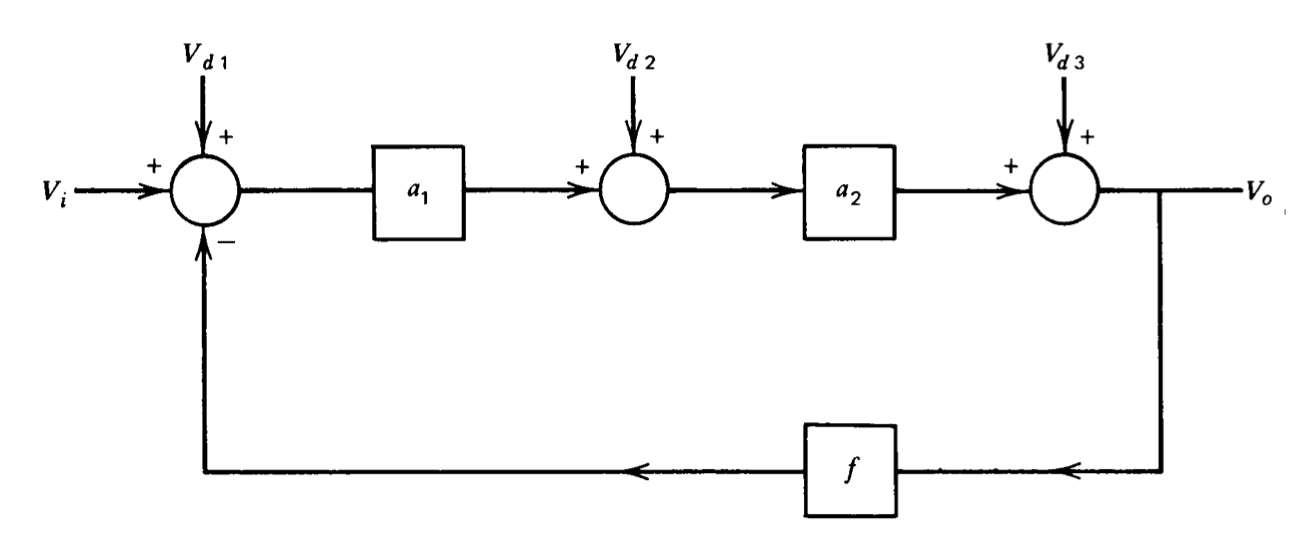
El lector debe convencerse de que el diagrama de bloques de la Figura 2.5 implica que el voltaje de salida está relacionado con la entrada y las perturbaciones como
\[V_o = \dfrac{a_1 a_2 [(V_i + V_{d1}) + (V_{d2}/a_1) + (V_{d3}/a_1 a_2)]}{1 + a_1 a_2 f} \nonumber \]
La ecuación 2.4 muestra que la perturbación no\(V_{d1}\) se atenúa en relación con la señal de entrada. Este resultado se espera desde entonces\(V_i\) y\(V_{d1}\) entrar al sistema en el mismo punto, y refleja el hecho de que la retroalimentación no puede mejorar cantidades como la cifra de ruido de un amplificador. Las perturbaciones que ingresan al amplificador en otros puntos se atenúan con respecto a la señal de entrada en cantidades iguales a las ganancias de trayectoria directa entre la entrada y los puntos donde se aplican las perturbaciones.
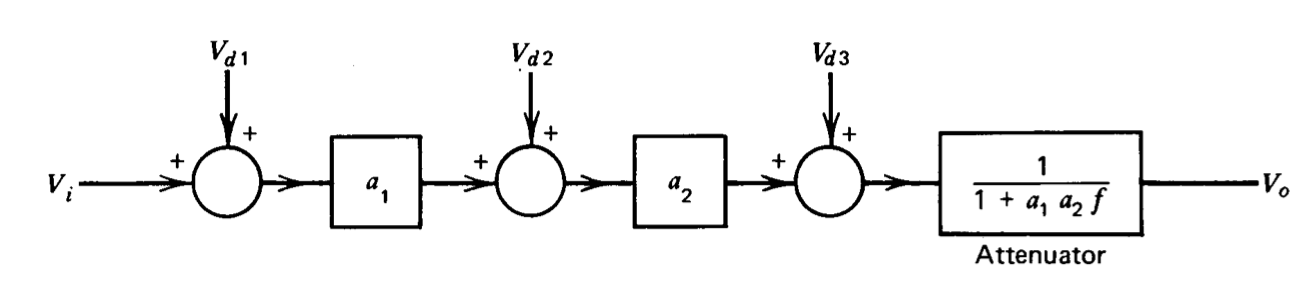
Es importante enfatizar que la ganancia de trayectoria de avance que precede a la perturbación, en lugar de la retroalimentación, da como resultado la atenuación relativa de la perturbación. Esta característica se ilustra en la Figura 2.6. Este sistema de bucle abierto, que sigue la trayectoria de avance de la Figura 2.5 con un atenuador, produce la misma salida que el sistema de retroalimentación de la Figura 2.5. El sistema de retroalimentación es casi siempre el enfoque más práctico, ya que el sistema de bucle abierto requiere grandes señales, con problemas concomitantes de saturación y disipación de potencia, en la entrada al atenuador. Por el contrario, la realización de retroalimentación limita las variables del sistema a niveles más realistas.
Resumen
Esta sección ha mostrado cómo se puede utilizar la retroalimentación para desensibilizar un sistema a cambios en los valores de los componentes o a perturbaciones aplicadas externamente. Esta desensitividad sólo se puede obtener a cambio de incrementos en las ganancias de diversos componentes del sistema. Existen numerosas situaciones en las que este tipo de comercio es ventajoso. Por ejemplo, puede ser posible reemplazar una etapa de salida lineal costosa en un amplificador de audio de alta fidelidad con una unidad más barata y compensar este cambio agregando una etapa económica de amplificación de bajo nivel.
Las impedancias de entrada y salida de los amplificadores también se modifican por retroalimentación. Por ejemplo, si la variable de salida que se retroalimenta es una tensión, la retroalimentación tiende a estabilizar el valor de esta tensión y reducir su dependencia de las corrientes de carga perturbadoras, lo que implica que la retroalimentación da como resultado una impedancia de salida más baja. Alternativamente, si la información realimentada es proporcional a la corriente de salida, la retroalimentación eleva la impedancia de salida. De manera similar, la retroalimentación puede limitar el voltaje de entrada o la corriente aplicada a un amplificador, dando como resultado una impedancia de entrada baja o alta respectivamente. Se reserva una discusión cuantitativa de este efecto para la Sección 2.5.
Una palabra de precaución es para moderar la impresión de que las mejoras en el rendimiento siempre acompañan a los aumentos en la magnitud de la transmisión de bucle. Desafortunadamente, la transmisión en bucle de un sistema no puede aumentarse sin límite, ya que una ganancia suficientemente alta invariablemente hace que un sistema se vuelva inestable. Un sistema estable se define como aquel para el cual se produce una salida acotada en respuesta a una entrada acotada. Por el contrario, un sistema inestable exhibe un comportamiento fuera de control u oscilatorio en respuesta a una entrada acotada. La inestabilidad ocurre en los sistemas de alta ganancia debido a que pequeños errores dan lugar a una gran acción correctiva. La propagación de señales alrededor del bucle se retrasa por la dinámica de los elementos en el bucle, y como consecuencia los sistemas de alta ganancia tienden a sobrecorregir. Cuando esta sobrecorrección produce un error mayor que el error de inicio, el.system es inestable.
Este importante aspecto del problema de retroalimentación no apareció en esta sección ya que se han ignorado las dinámicas asociadas a diversos elementos. El problema de la estabilidad se investigará en detalle en el Capítulo 4.


