2.5: Efectos de la retroalimentación sobre la impedancia de entrada y salida
- Page ID
- 84152
Los efectos estabilizadores de ganancia y linealización de la retroalimentación se han descrito anteriormente en este capítulo. La retroalimentación también tiene efectos importantes sobre las impedancias de entrada y salida de un amplificador, con el tipo de modificación dependiente de la topología de la combinación amplificador-red de retroalimentación.
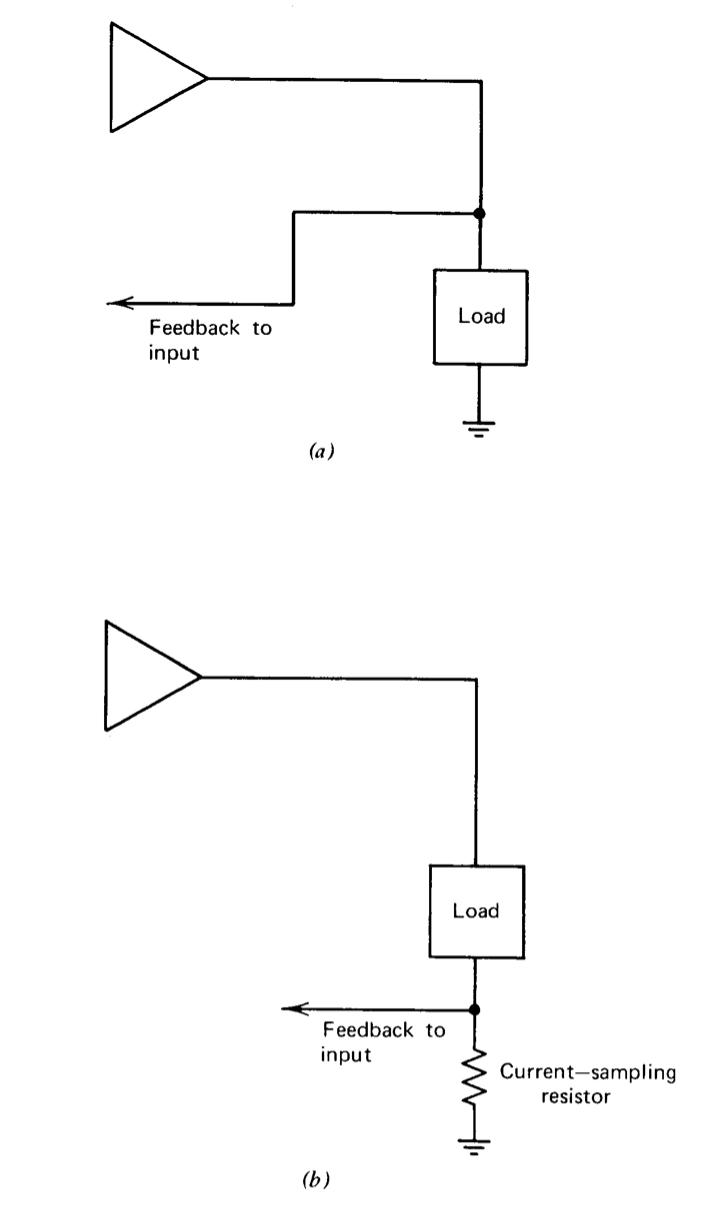
La Figura 2.15 muestra cómo se podría organizar la retroalimentación para devolver información sobre el voltaje aplicado a la carga o el flujo de corriente a través de ella. Es claro a partir de argumentos físicos que estas dos topologías de salida deben alterar la impedancia frente a la carga de diferentes maneras. Si la información realimentada a la entrada se refiere al voltaje de salida, la retroalimentación tiende a reducir los cambios en el voltaje de salida causados por perturbaciones (cambios en la corriente de carga), lo que implica que la impedancia de salida del amplificador mostrado en la Figura 2.15\(a\) se reduce por retroalimentación. Alternativamente, si se retroalimenta información sobre la corriente de carga, se reducen los cambios en la corriente de salida causados por perturbaciones (cambios en el voltaje de carga), lo que demuestra que este tipo de retroalimentación eleva la impedancia de salida.
En la Figura 2.16 se muestran dos topologías de entrada posibles. En la Figura 2.16\(a\), la señal de entrada se aplica en serie con la entrada diferencial del amplificador. Si las características del amplificador son satisfactorias, estamos seguros de que cualquier nivel de señal de salida requerido se puede lograr con una pequeña corriente de entrada del amplificador. Por lo tanto, la corriente requerida de la fuente de señal de entrada será pequeña, lo que implica una alta impedancia de entrada. La topología mostrada en la Figura 2.16\(b\) reduce la impedancia de entrada, ya que solo aparece una pequeña tensión a través de la conexión de entrada-señal paralela y amplificador-entrada.
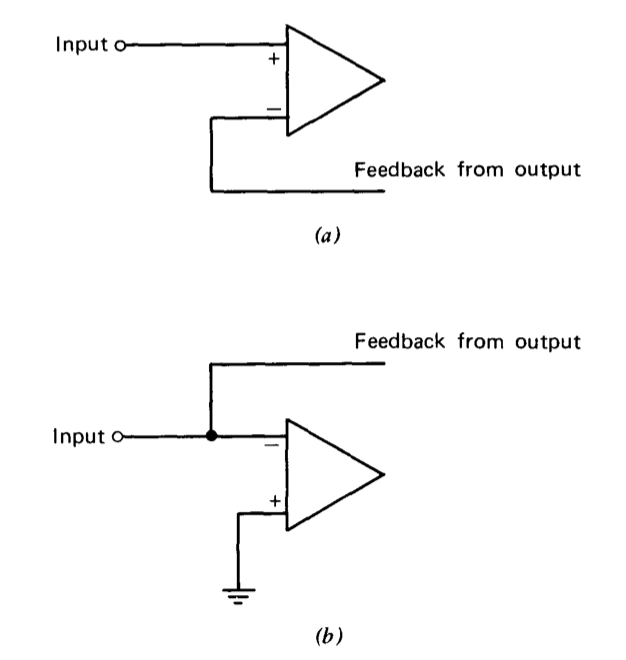
Figura 2.16 Dos topologías de entrada posibles. (\(a\)) Señal de entrada aplicada en serie con entrada de amplificador. (\(b\)) Señal de entrada aplicada en paralelo con la entrada del amplificador.
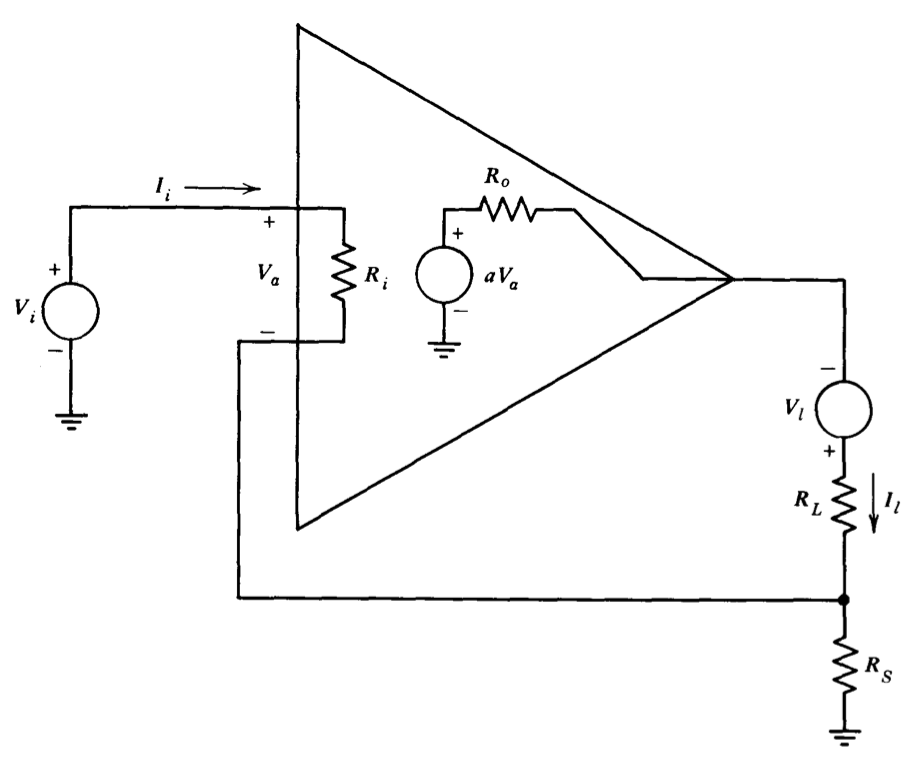
Figura 2.17 Amplificador con altas resistencias de entrada y salida.
La cantidad por la que la retroalimentación escala las impedancias de entrada y salida está directamente relacionada con la transmisión en bucle, como se muestra en el siguiente ejemplo. Un amplificador operacional conectado para altas resistencias de entrada y salida alta se muestra en la Figura 2.17. La resistencia de entrada para esta topología es simplemente la relación\(V_i/I_i\). La resistencia de salida se determina al incluir una fuente de voltaje en serie con la resistencia de carga y calculando la relación del cambio en el voltaje de esta fuente al cambio resultante en la corriente de carga,\(V_l/I_l\). Si se asume que los componentes de\(I_l\) y la corriente a través de la resistencia de muestreo\(R_S\) atribuibles a\(I_i\) son despreciables (lo que implica que el amplificador, en lugar de una red pasiva, proporciona ganancia del sistema) y eso\(R_i \gg R_s\), se aplican las siguientes ecuaciones.
\[V_a = V_i - R_S I_l \nonumber \]
\[I_l = \dfrac{aV_a + V_l}{R_o + R_L + R_S} \nonumber \]
\[I_i = \dfrac{V_a}{R_i} \nonumber \]
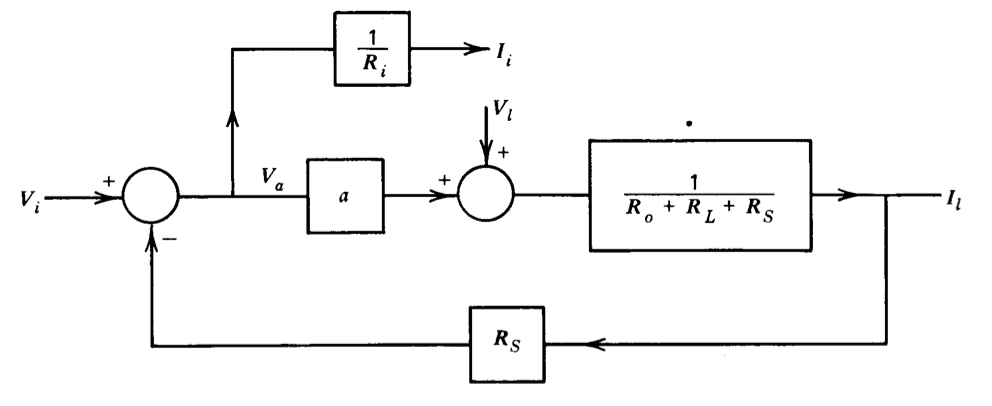
Estas ecuaciones se representan en forma de diagrama de bloques en la Figura 2.18. Este diagrama de bloques verifica el resultado anticipado de que, dado que el voltaje de entrada se compara con la corriente de salida muestreada a través de la resistencia\(R_S\), la transconductancia ideal (relación de\(I_l\) a\(V_i\)) es simplemente igual a\(G_S\). La resistencia de entrada se evalúa señalando que
\[\dfrac{I_i}{V_i} = \dfrac{1}{R_{in}} = \dfrac{1}{R_i \{1 + [aR_S/(R_o + R_L + R_S)]\}}\label{eq2.5.5} \]
o
\[R_{in} = R_i \left (1 + \dfrac{aR_S}{R_o + R_L + R_S} \right ) \nonumber \]
La resistencia de salida se determina a partir de (Tenga en cuenta que la resistencia de salida en este ejemplo se calcula incluyendo una fuente de voltaje en serie con la resistencia de carga. Este enfoque se utiliza para enfatizar que la transmisión de bucle que determina la resistencia de salida está influenciada por\(R_L\). Un desarrollo alternativo podría evaluar la resistencia frente a la carga\(R_L\) reemplazándola por un generador de prueba).
\[\dfrac{I_l}{V_l} = \dfrac{1}{R_{out}} = \dfrac{1}{(R_o + R_L + R_S) \{1 + [aR_S/(R_o + R_L + R_S)]\}} \nonumber \]
rindiendo
\[R_{out} = (R_o + R_L + R_S) \left (1 + \dfrac{aR_S}{R_o + R_L + R_S} \right ) \label{eq2.5.7} \]
Las características esenciales de las Ecuaciones\(\ref{eq2.5.5}\) y\(\ref{eq2.5.7}\) son las siguientes. Si el sistema no tiene retroalimentación (por ejemplo, si\(a = 0\)), las resistencias de entrada y salida se convierten en
\[R_{in}' = R_i \nonumber \]
y
\[R_{out}' = R_o + R_L + R_S \nonumber \]
La retroalimentación aumenta ambas cantidades por un factor de\(1 + [aR_S/ (R_o + R_L + R_S)]\), donde\(-aR_S/(R_o + R_L + R_S)\) se reconoce como la transmisión de bucle. Así vemos que las resistencias en este ejemplo se incrementan en el mismo factor (uno menos la transmisión en bucle) a medida que aumenta la desensitividad atribuible a la retroalimentación. El resultado es general, de manera que las impedancias de entrada o salida siempre se pueden calcular para las topologías mostradas en las figuras 2.15 o 2.16 encontrando la impedancia de interés sin retroalimentación y escalándola (arriba o abajo según topología) por un factor de uno menos la transmisión en bucle.
Si bien la retroalimentación ofrece un método conveniente para controlar las impedancias de entrada o salida del amplificador, resultados comparables (y en ciertos casos, superiores) son al menos conceptualmente posibles sin el uso de retroalimentación. Consideremos, por ejemplo, la Figura 2.19, que muestra tres formas de conectar un amplificador operacional para alta impedancia de entrada y ganancia de voltaje unitario.
La conexión del seguidor de la Figura 2.19\(a\) proporciona una ganancia de voltaje
\[\dfrac{V_o}{V_i} = \dfrac{a}{1 + a} \nonumber \]
o aproximadamente unidad para grandes valores de\(a\). La relación entre la impedancia de entrada y la transmisión en bucle discutida anteriormente en esta sección muestra que la impedancia de entrada para esta conexión es
\[\dfrac{V_i}{I_i'} = Z_i (1 + a) \nonumber \]
La conexión mostrada en la Figura 2.19b precede al amplificador con una impedancia que, en conjunto con la impedancia de entrada del amplificador, atenúa la señal de entrada por un factor de\(1/(1 + a)\). Esta atenuación se combina con la ganancia de voltaje del propio amplificador para proporcionar una ganancia de voltaje compuesta idéntica a la de la conexión del seguidor. De manera similar, la impedancia en serie del elemento de entrada del atenuador se suma a la impedancia de entrada del propio amplificador de manera que la impedancia de entrada de la combinación es idéntica a la del seguidor.
El uso de un transformador ideal como elemento modificador de impedancia puede conducir a una impedancia de entrada mejorada en comparación con el enfoque de retroalimentación. Con una relación de vueltas de transformador de\((a + 1): 1\), la ganancia de voltaje general de la combinación transformador-amplificador es la misma que la de la conexión del seguidor, mientras que la impedancia de entrada es
\[\dfrac{V_i}{I_i ''} = Z_i (1 + a)^2 \nonumber \]
Este valor supera en gran medida el valor obtenido con el seguidor para la ganancia de voltaje del amplificador grande.
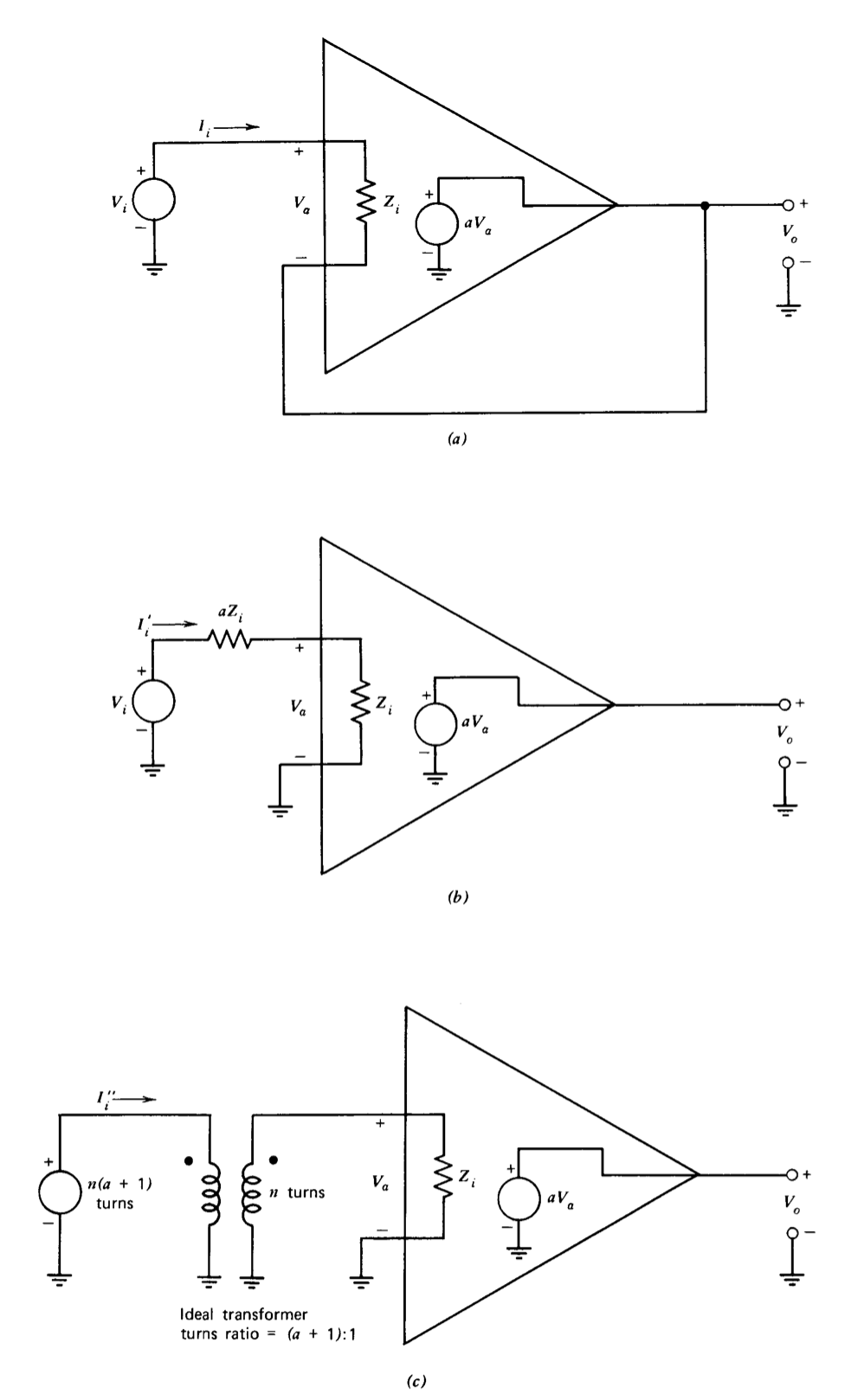
El propósito del ejemplo anterior ciertamente no es implicar que los atenuadores o transformadores deben usarse con preferencia a la retroalimentación para modificar los niveles de impedancia. Las desventajas prácticas asociadas con los dos enfoques anteriores, como la acentuación del ruido que acompaña a la gran atenuación de la señal de entrada y la característica de respuesta de frecuencia limitada de los transformadores, a menudo impiden su uso. El ejemplo, sin embargo, sirve para ilustrar que es realmente la ganancia de potencia del amplificador, más que el uso de retroalimentación, lo que conduce al escalado de impedancia. Podemos enfatizar aún más este punto al señalar que la impedancia de entrada de la conexión del amplificador se puede aumentar sin límite siguiéndola con un transformador elevador y aumentando la atenuación de voltaje ya sea de la red o del transformador que precede al amplificador para que la ganancia general sea una. Esta observación es un reflejo del hecho de que el amplificador por sí solo proporciona ganancia de potencia infinita ya que tiene impedancia de salida cero.
Una manera más bien filosófica de aceptar esta realidad sobre el escalado de impedancia es darse cuenta de que la retroalimentación se usa con mayor frecuencia debido a su ventaja fundamental de reducir la sensibilidad de un sistema a los cambios en la ganancia de su elemento de ruta de avance. Las ventajas del escalado de impedancia se pueden obtener además de la desensitividad simplemente eligiendo una topología adecuada.
PROBLEMAS
Ejercicio\(\PageIndex{1}\)
La Figura 2.20 muestra un diagrama de bloques para un sistema de retroalimentación lineal. Escriba un conjunto completo e independiente de ecuaciones para las relaciones que implica este diagrama. Resuelve tu conjunto de ecuaciones para determinar la ganancia de entrada a salida del sistema.
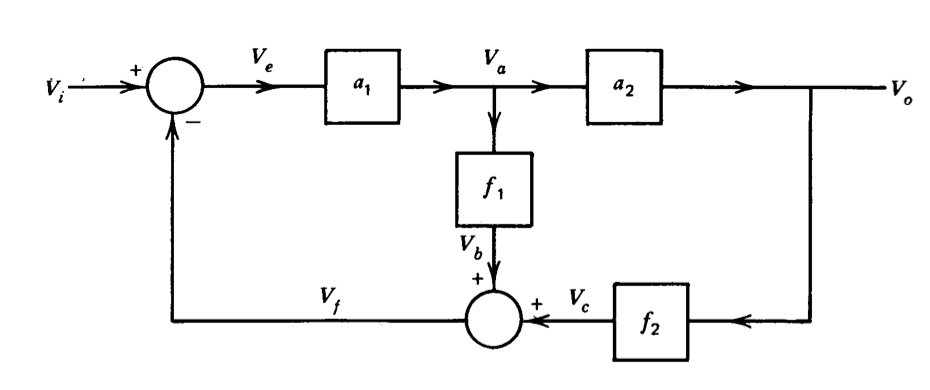
Ejercicio\(\PageIndex{2}\)
Determinar cómo el cambio fraccionario en la ganancia de bucle cerrado
\[\dfrac{d(V_o/V_i)}{V_o/V_i}\nonumber \]
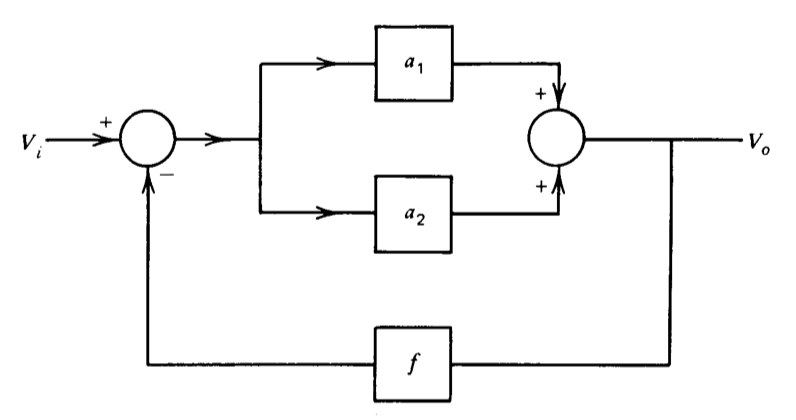
se relaciona con cambios fraccionarios en\(a_1, a_2\), y\(f\) para el sistema mostrado en la Figura 2.21.
Ejercicio\(\PageIndex{3}\)
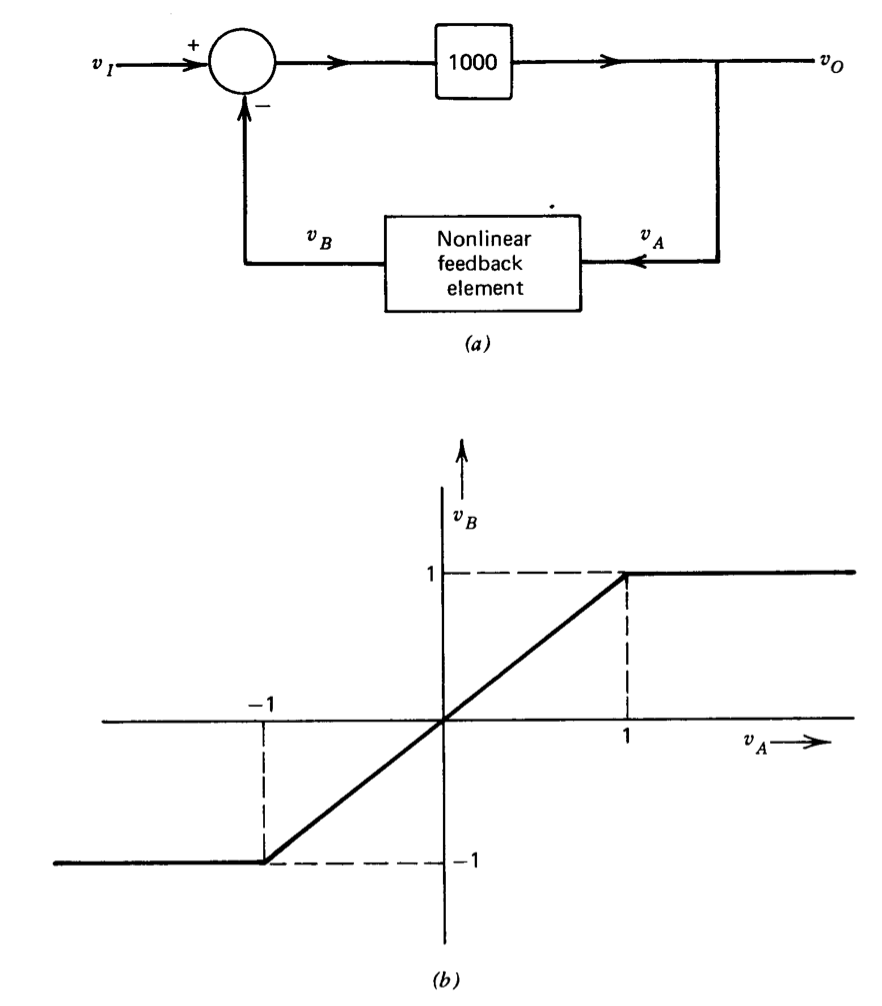
Trazar las características de transferencia de bucle cerrado para el sistema no lineal mostrado en la Figura 2.22.
Ejercicio\(\PageIndex{4}\)
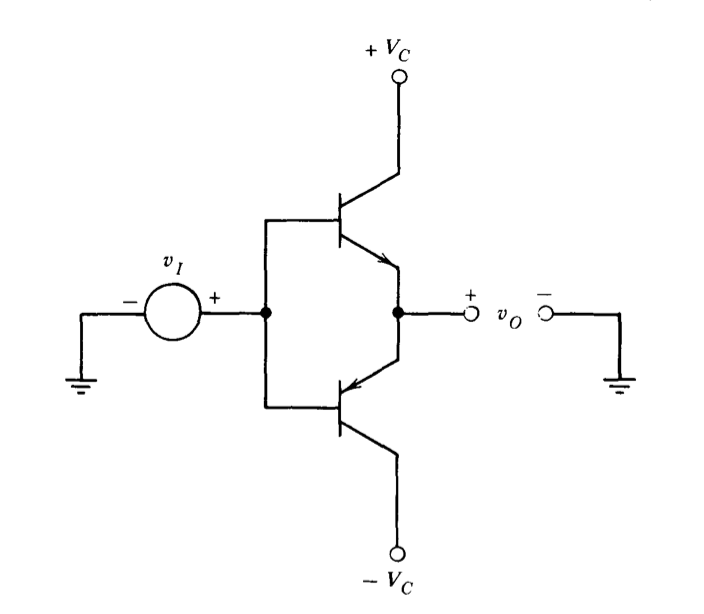
La conexión emisor-seguidor complementaria mostrada en la Figura 2.23 es una etapa simple de unidad-voltaje-ganancia que tiene una ganancia de potencia aproximadamente igual a la ganancia de corriente de los transistores utilizados. Tiene características de transferencia no lineal, ya que es necesario aplicar aproximadamente 0.6 voltios a la unión base-emisor de un transistor de silicio para iniciar la conducción.
(a) Aproximar las características de transferencia de entrada-salida para la etapa de seguidor de emisor.
(b) Diseñar un circuito que combine esta etapa de potencia con un amplificador operacional y cualquier componente pasivo necesario para proporcionar una ganancia de bucle cerrado con un valor ideal de +5.
(c) Aproximar las características reales de entrada-salida de su circuito de retroalimentación asumiendo que la ganancia de bucle abierto del amplificador operacional es\(10^5\).
Ejercicio\(\PageIndex{5}\)
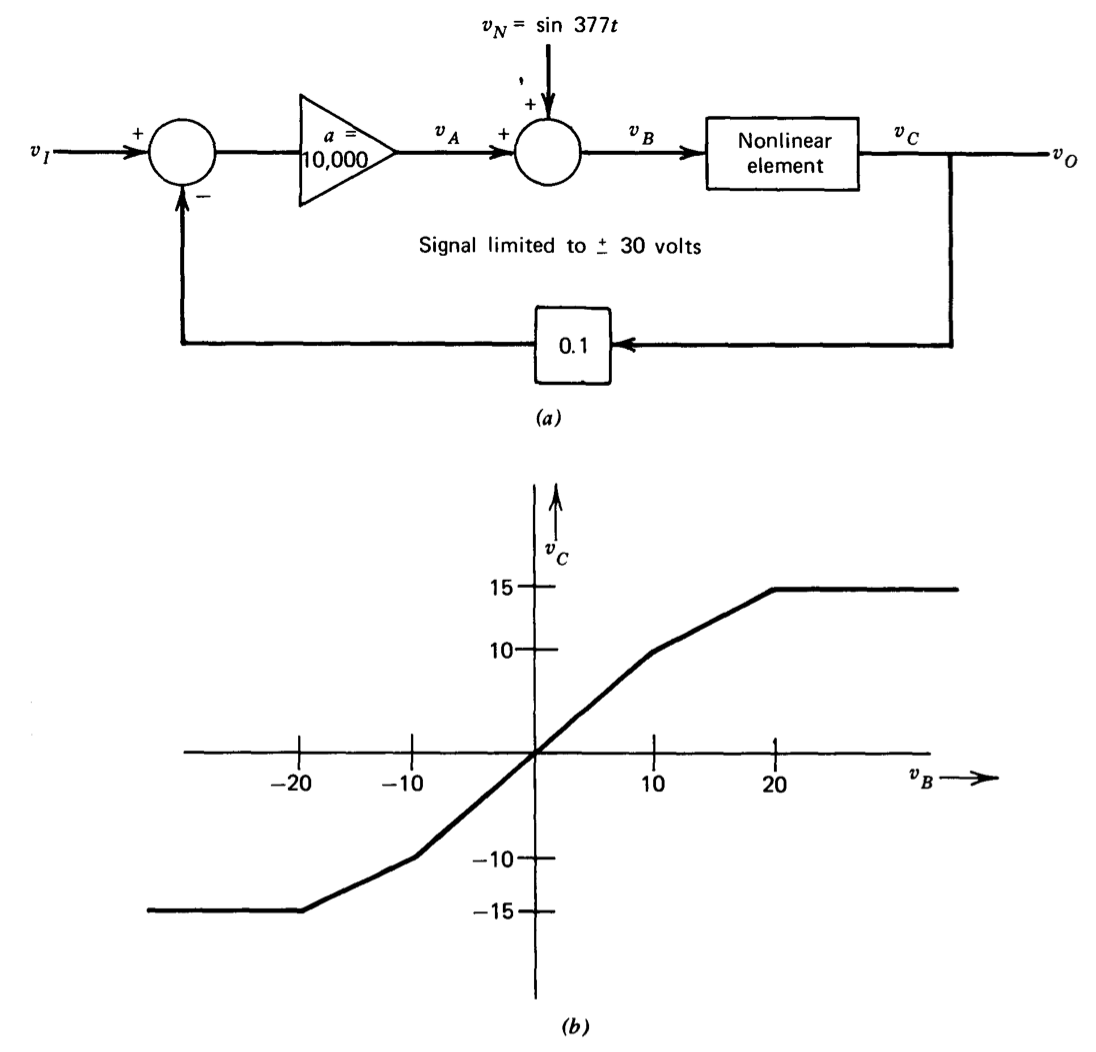
(a) Determinar la ganancia incremental\(v_o/v_i\) para\(V_I = 0.5\) y 1.25 para el sistema mostrado en la Figura 2.24.
(b) Estimar la señal\(v_A\) para\(v_I\), una rampa de unidad\([v_I (t) = 0, t < 0, = t, t > 0]\).
(c) Para\(v_I = 0\), determinar la amplitud de la componente sinusoidal de\(v_O\).
Ejercicio\(\PageIndex{6}\)
Determinar\(V_o\) como una función de\(V_{i1}\) y\(V_{i2}\) para el sistema de retroalimentación mostrado en la Figura 2.25.
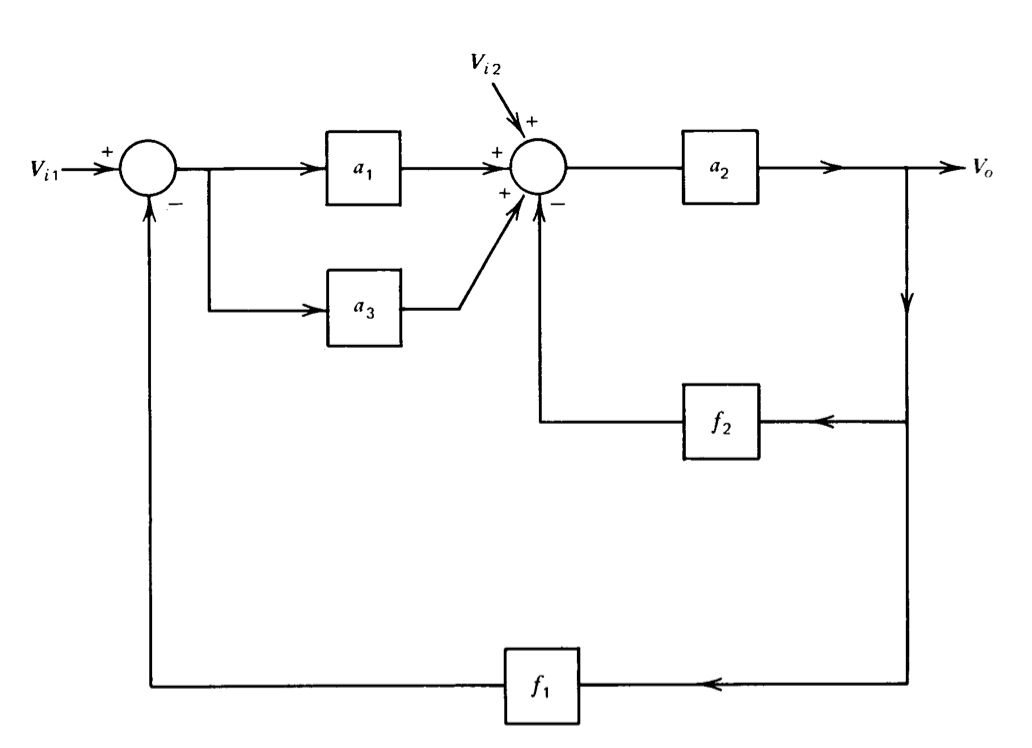
Ejercicio\(\PageIndex{7}\)
Dibuje un diagrama de bloques que relacione el voltaje de salida con el voltaje de entrada para un seguidor de emisor. Puede suponer que el transistor permanece lineal, y usarun modelo híbrido pi para el dispositivo. Incluye elementos\(r_{\pi}\),\(r_x\)\(C_{\pi}\),, y\(C_{\mu}\), además del generador dependiente, en tu modelo. Reduzca el diagrama de bloques a una única función de transferencia de entrada-salida.
Ejercicio\(\PageIndex{8}\)
Dibuje un diagrama de bloques que se\(V_o\)\(V_i\) relacione con para la conexión no inversora mostrada en la Figura 2.26. También use técnicas de diagrama de bloques para determinar la impedancia en la salida, asumiendo que\(Z_i\) es muy grande.
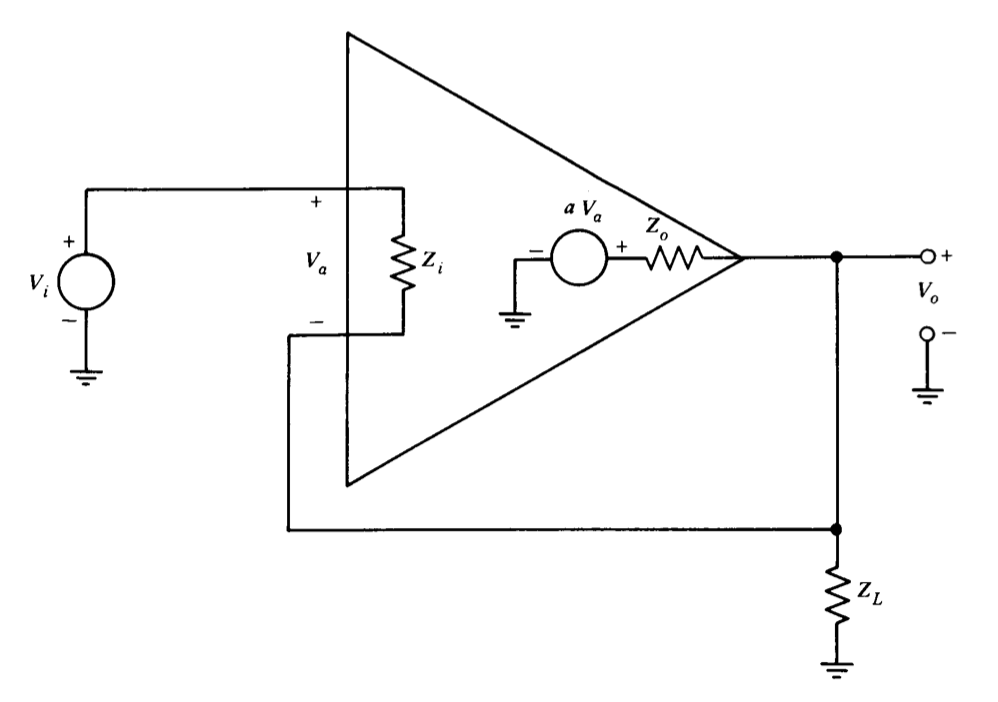
Ejercicio\(\PageIndex{9}\)
En la Figura 2.27 se muestra un sistema de retroalimentación negativa utilizado para rotar una antena de techo\(a\).
La inercia total del miembro de salida (antena, armadura del motor y limpiaparabrisas) es 2\(kg \cdot m^2\). El motor se puede modelar como una resistencia en serie con un generador de voltaje dependiente de la velocidad (Figura 2.27\(b\)).
El par proporcionado por el motor que acelera la inercia total del miembro de salida es de 10\(N \cdot m\) por amperio de\(I_a\). La polaridad del motor de generador pendiente es tal que tiende a reducir el valor de\(I_a\), a medida que el motor acelera de manera que\(I_a\), se vuelve cero para una velocidad del eje del motor igual a\(V_m/10\) radianes por segundo.
Dibuja un diagrama de bloques que se\(\theta_o\) relacione con\(\theta_i\). Puede incluir tantas variables intermedias como desee, pero asegúrese de incluir\(V_m\) y\(I_a\) en su diagrama. Encuentra la función de transferencia\(\theta_o/\theta_i\).
Modifique su diagrama para incluir una perturbación de salida aplicada a la antena por el viento. Calcular el error angular que resulta de una\(N \cdot m\) perturbación de 1.
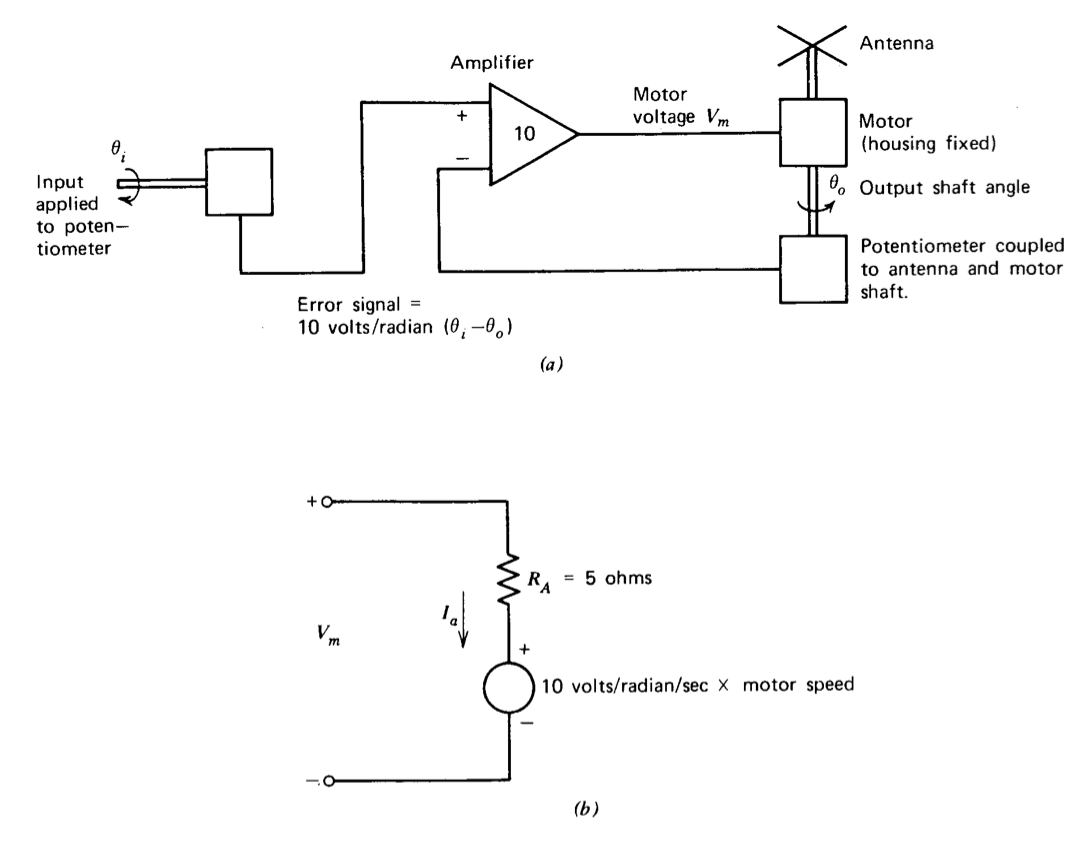
Ejercicio\(\PageIndex{10}\)
Dibuja un diagrama de bloques para este conjunto de ecuaciones:
\[\begin{array} {rcl} {W + X} & = & {3} \\ {X + Y} & = & {5} \\ {Y + Z} & = & {7} \\ {2W + X + Y + Z} & = & {11} \end{array}\nonumber \]
Utilice la ecuación de reducción de diagrama de bloques (Ecuación 2.4.18) para determinar los valores de las cuatro variables dependientes.
Ejercicio\(\PageIndex{11}\)
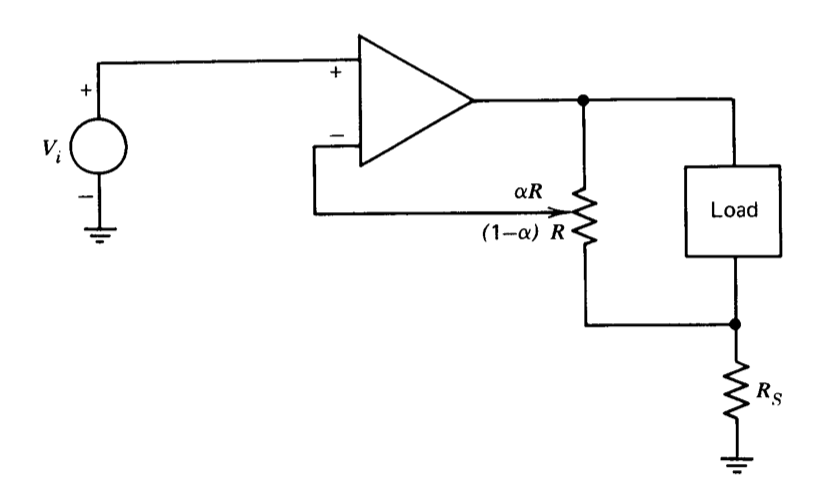
La conexión que se muestra en la Figura 2.28 retroalimenta información sobre la corriente de carga y el voltaje de carga a la entrada del amplificador. Dibuja un gramo de diámetro de bloque que le permita calcular la resistencia de salida\(V_o/I_d\).
Se puede suponer que\(R \gg R_S\) y que la carga se puede modelar como una resistencia\(R_L\). ¿Cuál es la resistencia de salida para muy grandes\(a\)?
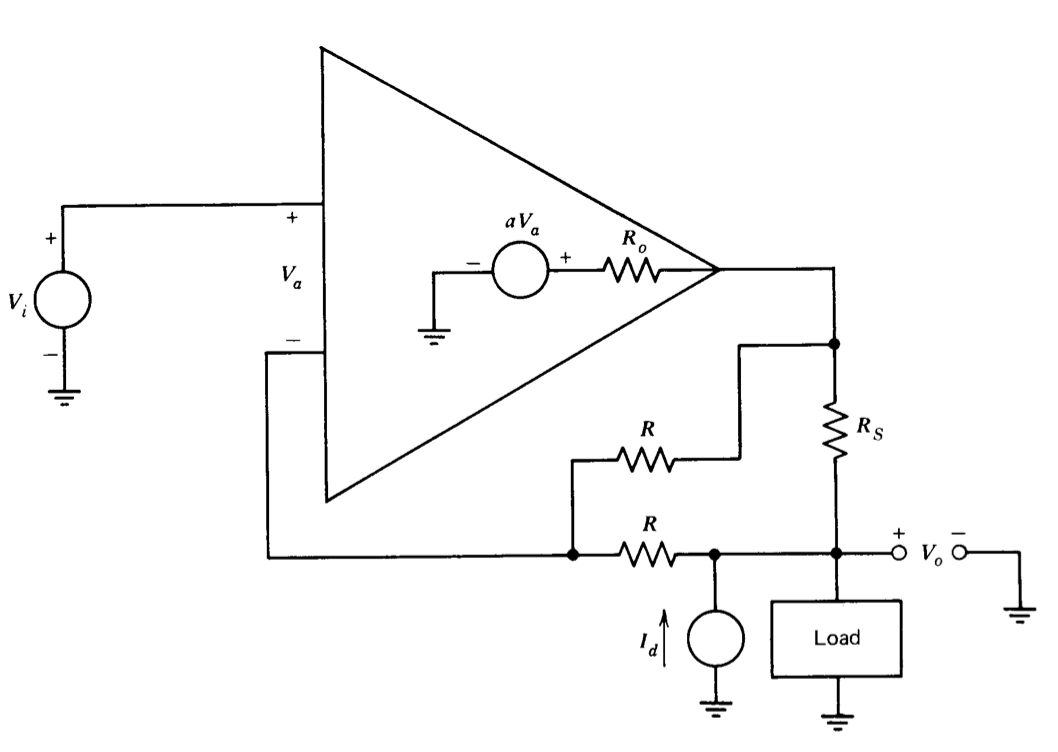
Ejercicio\(\PageIndex{12}\)
Un amplificador operacional conectado para proporcionar una resistencia de salida ajustable se muestra en la Figura 2.29. Encuentre un circuito equivalente a Thevenin frente a la carga en función del ajuste del potenciómetro a. puede suponer que la resistencia\(R\) es muy grande y que el amplificador operacional tiene características ideales.