3.5: Relaciones entre la respuesta transitoria y la respuesta de frecuencia
- Page ID
- 84207
Es claro que bien la respuesta de impulso (o la respuesta a cualquier otra entrada transitoria) de un sistema lineal o su respuesta de frecuencia caracterizan completamente al sistema. En muchos casos, las mediciones experimentales en un sistema de bucle cerrado se realizan más fácilmente aplicando una entrada transitoria. Podemos, sin embargo, estar interesados en ciertos aspectos de la respuesta de frecuencia del sistema como su ancho de banda definido como la frecuencia donde su ganancia cae a 0.707 del valor de frecuencia media.
Dado que la respuesta transitoria o la respuesta de frecuencia caracterizan completamente al sistema, debería ser posible determinar el rendimiento en un dominio a partir de mediciones realizadas en el otro. Desafortunadamente, dado que la respuesta transitoria medida no proporciona una ecuación para esto
respuesta, las técnicas de Laplace no se pueden usar directamente a menos que la respuesta de tiempo se aproxime primero analíticamente en función del tiempo. Esta sección enumera varias relaciones aproximadas entre la respuesta transitoria y la respuesta de frecuencia que se pueden utilizar para estimar una medida de desempeño de la otra. Las aproximaciones se basan en las propiedades de los sistemas de primer y segundo orden.
Se supone que la ruta de retroalimentación para el sistema en estudio es independiente de la frecuencia y tiene una magnitud de unidad. Un sistema con una ruta de retroalimentación independiente de la frecuencia fo puede manipularse como se muestra en la Figura 3.16 para producir un sistema de retroalimentación unitaria escalado. Las aproximaciones dadas son válidas para la función de transferencia\(V_a/V_i\), y se\(V_o\) pueden determinar escalando valores para\(V_a\) by\(1/f_o\).
También se supone que la magnitud de la transmisión de bucle d-c es muy grande, de modo que la ganancia de bucle cerrado es casi una en d-c. Se supone además que la singularidad más cercana al origen en el plano s es un polo o un par complejo de polos, y que el número de polos de la función excede
el número de ceros. Si se satisfacen estas suposiciones, muchos sistemas prácticos tienen relaciones entre el dominio del tiempo y el dominio de la frecuencia similares a las de los sistemas de primer o segundo orden.
Los parámetros que usaremos para describir la respuesta transitoria y la respuesta de frecuencia de un sistema incluyen los siguientes.
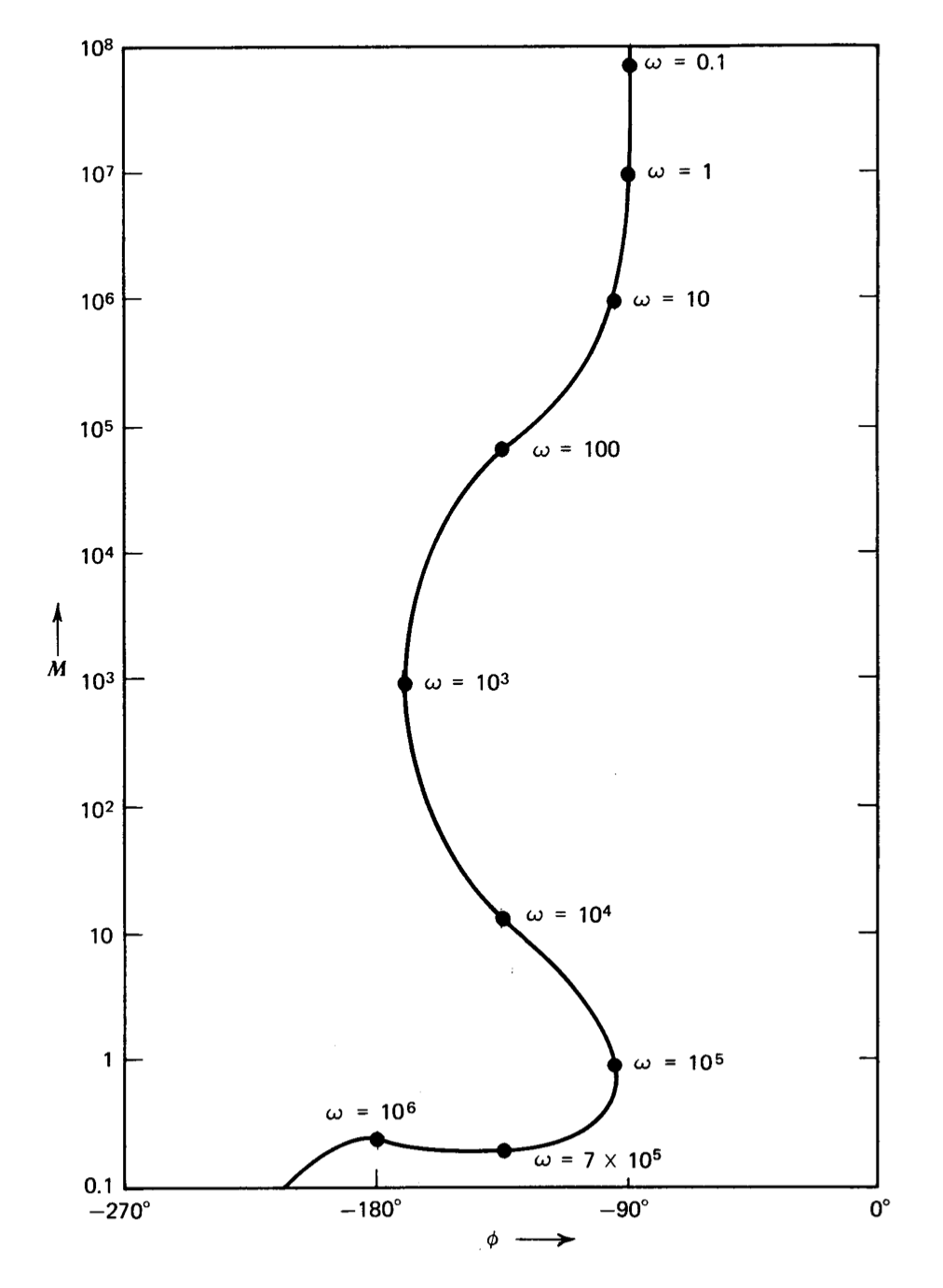
Figura 3.15 Gráfica de fase de ganancia de\(\dfrac{10^7 (10^{-4} s + 1)}{s(0.1s + 1)(s^2/10^{12} + 2 (0.2) s/10^6 + 1)}\).
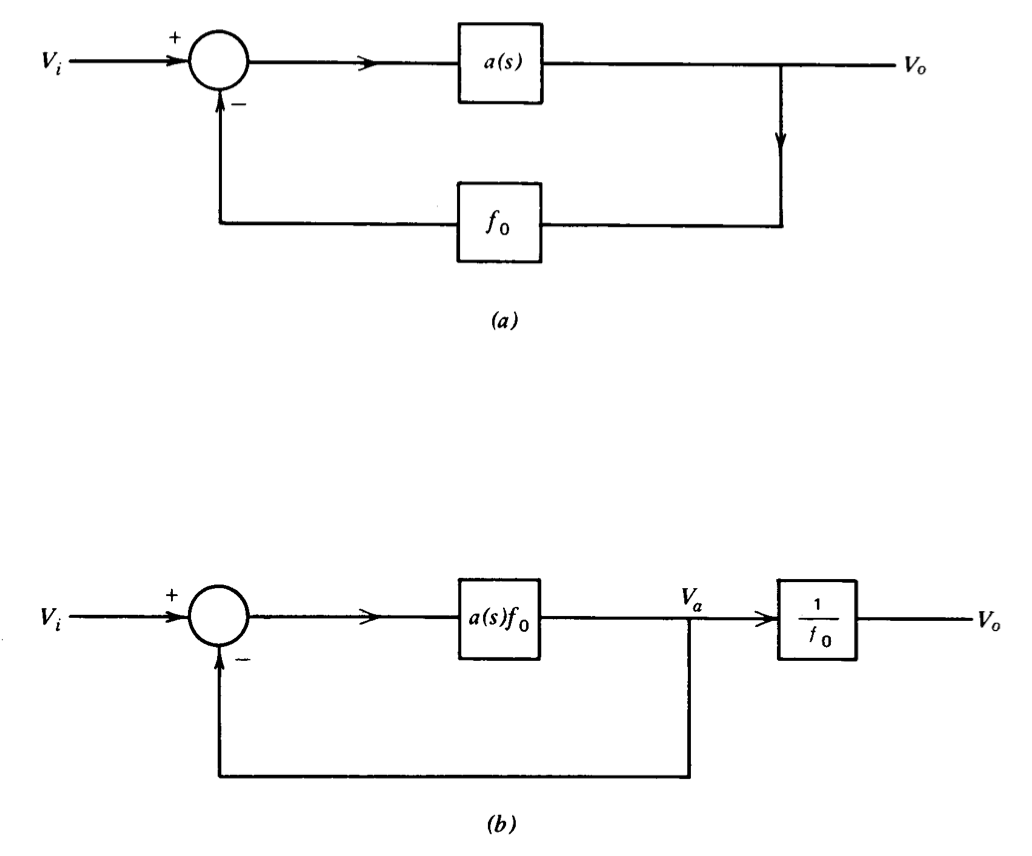
Figura 3.16 Topología del sistema para relaciones aproximadas. (\(a\)) Sistema con ruta de retroalimentación independiente de la frecuencia. (\(b\)) Sistema representado en forma escalada, unidad-retroalimentación.
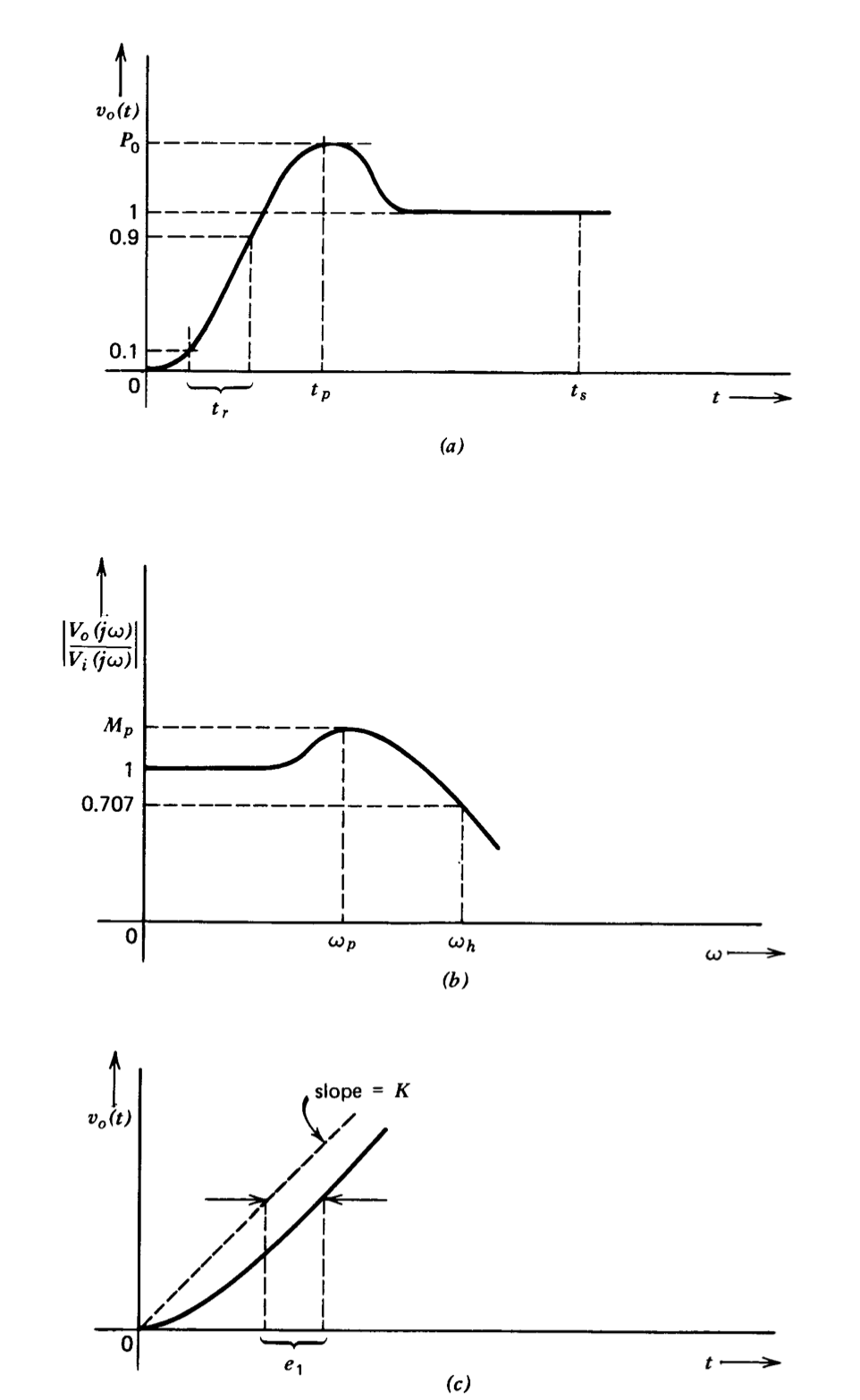
a) Tiempo de ascenso\(t_r\). El tiempo requerido para que la respuesta escalonada pase del 10 al 90% del valor final.
b) El valor máximo de la respuesta escalonada\(P_0\).
c) El momento en que\(P_0\) se produzca\(t_p\).
d) Tiempo de sedimentación\(t_s\). El tiempo después del cual la respuesta de paso del sistema permanece dentro del 2% del valor final.
e) El coeficiente de error ei. (Ver Sección 3.6.) Este coeficiente es igual al retardo de tiempo entre la salida y la entrada cuando el sistema ha alcanzado condiciones de estado estacionario con una rampa como entrada.
(f) El ancho de banda en radianes por segundo\(w_h\) o hercios\(f_h\) (\(f_h = \omega_h/2\pi\)). La frecuencia a la que la respuesta del sistema es 0.707 de su valor de baja frecuencia.
g) La magnitud máxima de la respuesta de frecuencia\(M_p\).
(h) La frecuencia a la que\(M_p\) ocurre\(\omega_p\).
Estas definiciones se ilustran en la Figura 3.17.
Para un sistema de primer orden con\(V_o (s)/V_i (s) = 1/(\tau s + 1)\), las relaciones son
\[t_r = 2.2 \tau = \dfrac{2.2}{\omega_h} = \dfrac{0.35}{f_h}\label{eq3.5.1} \]
\[P_0 = M_p = 1 \nonumber \]
\[t_p = \infty \nonumber \]
\[t_s = 4\tau \nonumber \]
\[e_1 = \tau \nonumber \]
\[\omega_p = 0 \nonumber \]
Para un sistema de segundo orden con\(V_o (s)/V_i (s) = 1/(s^2/\omega_n^2 + 2 \zeta s/\omega_n + 1)\) y\(\theta \triangleq \cos^{-1} \zeta\) (ver Figura 3.7) las relaciones son
\[t_r \simeq \dfrac{2.2}{\omega_h} = \dfrac{0.35}{f_h}\label{eq3.5.7} \]
\[P_0 = 1 + \exp \dfrac{-\pi \zeta}{\sqrt{1 - \zeta^2}} = 1 + e^{-\pi/\tan \theta}. \nonumber \]
\[t_p = \dfrac{\pi}{\omega_n \sqrt{1 - \zeta^2}} = \dfrac{\pi}{\omega_n \sin \theta} \nonumber \]
\[t_s \simeq \dfrac{4}{\zeta \omega_n} = \dfrac{4}{\omega_n \cos \theta} \nonumber \]
\[e_1 = \dfrac{2 \zeta}{\omega_n} = \dfrac{2\cos \theta}{\omega_n} \nonumber \]
\[M_p = \dfrac{1}{2\zeta \sqrt{1 - \zeta^2}} = \dfrac{1}{\sin 2 \theta} \ \ \zeta < 0.707, \theta > 45^{\circ} \nonumber \]
\[\omega_p = \omega_n \sqrt{1 - 2\zeta^2} = \omega_n \sqrt{-\cos 2\theta} \ \ \zeta < 0.707, \theta > 45^{\circ} \nonumber \]
\[\omega_h = \omega_n (1 - 2 \zeta^2 + \sqrt{2 - 4\zeta^2 + 4\zeta^4})^{1/2} \nonumber \]
Si una respuesta de paso del sistema o respuesta de frecuencia es similar a la de un sistema de aproximación (véanse las figuras 3.6, 3.8, 3.11 y 3.12)\(t_r\), las mediciones de\(P_0\), y\(t_p\) permiten la estimación de\(\omega_h\)\(\omega_p\), y\(M_p\) o viceversa. El error de estado estacionario en respuesta a una rampa unitaria se puede estimar a partir de cualquier conjunto de mediciones.
Un comentario final sobre la calidad de la relación entre 0.707 ancho de banda y 10 a 90% step risetime (Ecuaciones\(\ref{eq3.5.1}\) y\(\ref{eq3.5.7}\)) está en orden. Para prácticamente cualquier sistema que satisfaga los supuestos originales, independientemente del orden o estabilidad relativa del sistema, el producto\(t_rf_h\) se encuentra dentro de unos pocos por ciento de 0.35. Esta relación es tan precisa que realmente no vale la pena medir\(f_h\) si la respuesta escalonada se puede determinar más fácilmente.


