3.6: COeficientes de error
- Page ID
- 84194
La respuesta de un sistema lineal a ciertos tipos de entradas transitorias puede ser difícil o imposible de determinar mediante técnicas de Laplace, ya sea porque la transformación del transitorio sea engorrosa de evaluar o porque el transitorio viola las condiciones necesarias para que exista su transformación. Por ejemplo, considere el ángulo que realiza una antena de radar con una referencia fija mientras rastrea una aeronave, como se muestra en la Figura 3.18. El ángulo de apuntamiento determinado a partir de la geometría es
\[\theta = \tan^{-1} \left [\dfrac{v}{l} t \right ]\label{eq3.6.1} \]
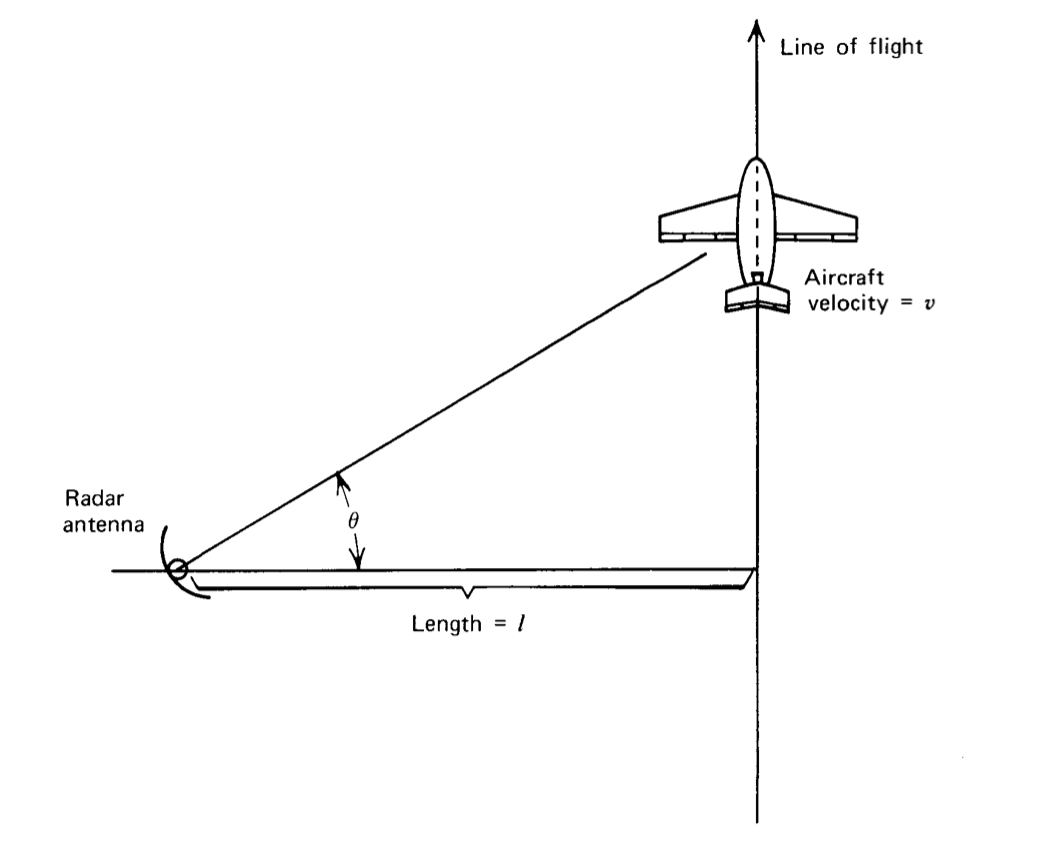
asumiendo que\(\theta = 0\) en\(t = 0\). Esta función no es transformable usando nuestra forma de la transformada de Laplace, ya que es distinta de cero para el tiempo negativo y dado que ninguna cantidad de desplazamiento de tiempo la hace cero para el tiempo negativo. La expansión introducida en esta sección proporciona un método conveniente para evaluar el desempeño de los sistemas excitados por entradas transitorias, como la Ecuación\(\ref{eq3.6.1}\), para la cual existen todas las derivadas en todo momento.
Serie de errores
Considera un sistema, inicialmente en reposo e impulsado por una sola entrada, con una función de transferencia\(G(s)\). Además, supongamos que se\(G(s)\) puede expandir en una serie de potencia en\(s\), o que
\[G(s) = g_0 + g_1 s + g_2 s^2 + \cdots + \label{eq3.6.2} \]
Si el sistema está excitado por una entrada\(v_i(t)\), la señal de salida en función del tiempo es
\[v_o (t) = \mathcal{L}^{-1} [G(s) V_i (s)] = \mathcal{L} [g_0 V_i (s) + g_1 s V_i (s) + g_2 s^2 V_i (s) + \cdots +] \nonumber \]
Si Ecuación\(\ref{eq3.6.2}\) es transformada inversa término por término, y la propiedad de diferenciación de las transformaciones de Laplace se usa para simplificar el resultado, vemos que (Un desarrollo matemáticamente satisfactorio se da en G. C. Newton, Jr., L. A. Gould, y J. F. Kaiser, Analytical Design of Lineal Feedback Controls, Wiley, Nueva York, 1957, Apéndice C. En esta referencia también se da una expresión que limita el error cuando se trunca la serie.)
\[v_o (t) = g_0 v_i (t) + g_1 \dfrac{dv_i (t)}{dt} + g_t \dfrac{d^2 v_i (t)}{dt^2} + \cdots + \label{eq3.6.4} \]
La serie completa arroja el valor correcto para los casos\(v_o(t)\) en que la función\(v_1(t)\) y todas sus derivadas existan en todo momento.
En la práctica, el método se utiliza normalmente para evaluar el error (o diferencia entre la salida ideal y real) que resulta para una entrada especificada. Si Ecuación\(\ref{eq3.6.4}\) se reescribe usando el error\(e(t)\) como parámetro dependiente, la serie resultante
\[e(t) = e_0 v_i (t) + e_1 \dfrac{dv_i (t)}{dt} + e_2 \dfrac{d^2 v_i (t)}{dt^2} + \cdots + \nonumber \]
se llama serie de errores, y los\(e\) s en el lado derecho de esta ecuación se denominan coeficientes de error.
Los coeficientes de error se pueden obtener mediante dos métodos de expansión equivalentes. Un enfoque matemático formal muestra que
\[e_k = \dfrac{1}{k!} \dfrac{d^k}{ds^k} \left [\dfrac{V_e (s)}{V_i (s)} \right ]_{s = 0} \nonumber \]
donde\(V_e (s)/ V_i (s)\) está la función de transferencia de entrada a error para el sistema. Alternativamente, la división sintética se puede usar para escribir la función de transferencia de entrada a error como una serie en potencias ascendentes de\(s\). El coeficiente del término sk en esta serie es\(e_k\).
Si bien las matemáticas formales requieren que se utilice la serie completa para determinar el error, la serie converge rápidamente en casos de interés práctico donde el error es pequeño en comparación con la señal de entrada. (Tenga en cuenta que si el error es del mismo orden de magnitud que la señal de entrada en un sistema de retroalimentación unitaria, se pueden obtener resultados comparables apagando el sistema). Así, en aplicaciones razonables, unos pocos términos de la serie de errores normalmente bastan. Además, el requisito de que existan todas las derivadas de la señal de entrada puede ser generalmente relajado si estamos interesados en errores en momentos separados de los tiempos de discontinuidades por al menos el tiempo de establecimiento del sistema. (Véase la Sección 3.5 para una definición del tiempo de asentamiento.)
Ejemplos
Algunas propiedades importantes de los amplificadores de retroalimentación se pueden ilustrar aplicando métodos de análisis de coeficientes de error a la conexión de amplificador inversor que se muestra en la Figura 3.19\(a\). En la Figura 3.19 se muestra un diagrama de bloques obtenido asumiendo una carga insignificante en la entrada y salida del amplificador\(b\). En este diagrama se genera una señal de error comparando la salida real del amplificador con el valor ideal,\(- V_i\). La función de transferencia de entrada a error de este diagrama de bloques es
\[\dfrac{V_e (s)}{V_i (s)} = \dfrac{-1}{1 + a(s)/2} \nonumber \]
Los amplificadores operacionales se diseñan frecuentemente para tener una función de transferencia de bucle abierto aproximadamente unipolar, lo que implica
\[a(s) \simeq \dfrac{a_0}{\tau s + 1} \nonumber \]
Los coeficientes de error asumiendo este valor para\(a(s)\) son fácilmente evaluados por medio de división sintética ya que
\[\begin{array} {rcl} {\dfrac{V_e (s)}{V_i (s)}} & = & {\dfrac{-1}{1 + a_0/2 (\tau s + 1)} = \dfrac{-2 - 2 \tau s}{a_0 + 2 + 2 \tau s}} \\ {} & = & {-\dfrac{2}{a_0 + 2} - \dfrac{2\tau}{a_0 + 2} \left (1 - \dfrac{2}{a_0 + 2} \right ) s + \dfrac{4\tau^2}{(a_0 + 2)^2} \left (1 - \dfrac{2}{a_0 + 2} \right ) s^2 + \cdots +} \end{array} \nonumber \]
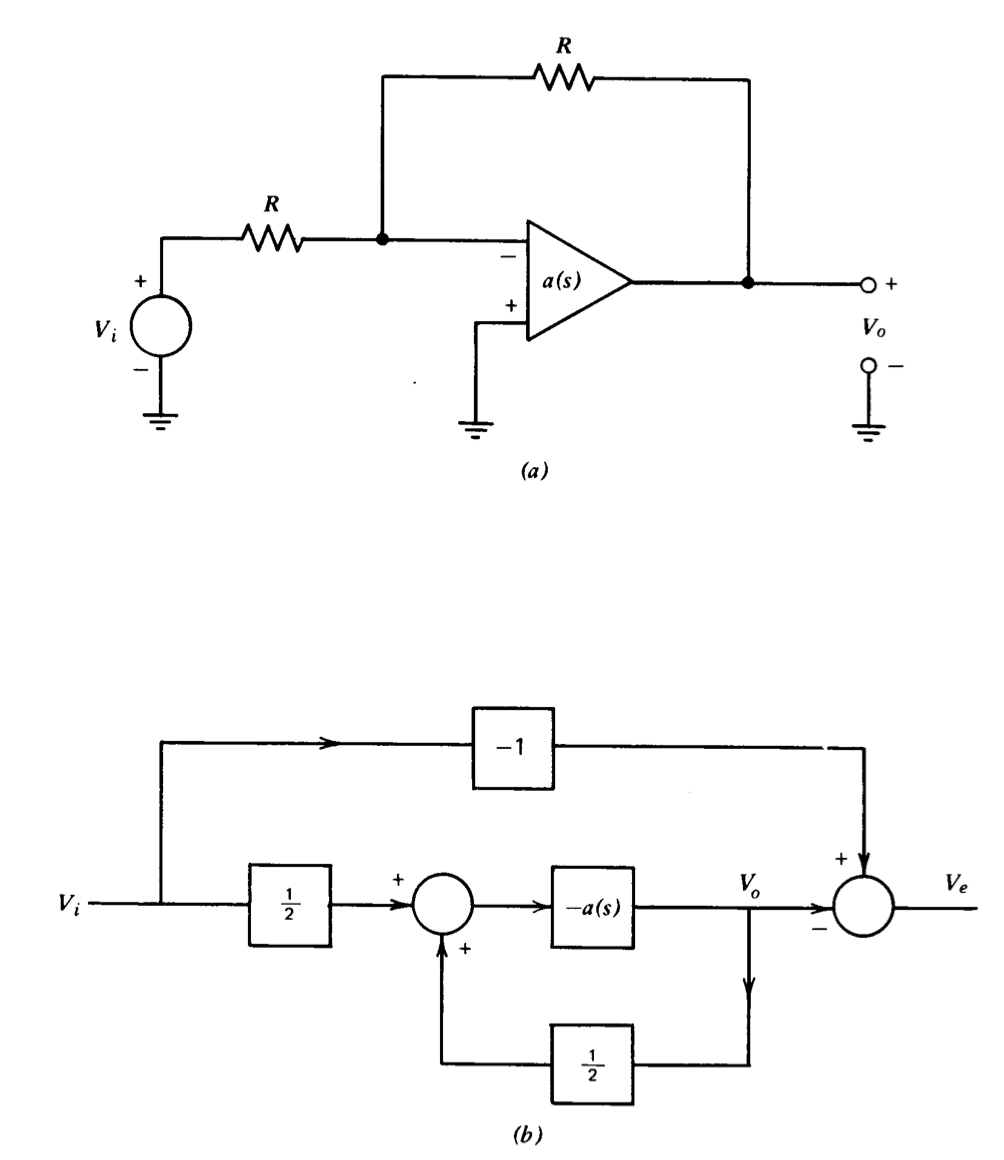
Si\(a_0\), la ganancia del amplificador d-c, es grande, los coeficientes de error son
\[\begin{array} {rcl} {e_0} & \simeq & {-\dfrac{2}{a_0}} \\ {e_1} & \simeq & {-\dfrac{2\tau}{a_0}} \\ {e_2} & \simeq & {\dfrac{4\tau^2}{a_0^2}} \\ {} & \cdot & {} \\ {} & \cdot & {} \\ {} & \cdot & {} \\ {e_n} & = & {\dfrac{(-2)^n r^n}{a_0^n} \ \ n \ge 1} \end{array} \nonumber \]
Los coeficientes de error se interpretan fácilmente en términos de la transmis sión de bucle de la combinación amplificador-red de retroalimentación en este ejemplo. La magnitud del coeficiente de error de orden cero es igual al recíproco de la transmisión del bucle d-c. La magnitud del coeficiente de error de primer orden es igual al recíproco de la frecuencia (en radianes por segundo) a la que la transmisión de bucle es unidad, mientras que la magnitud de cada coeficiente de error de orden superior posterior se atenúa por un factor igual a esta frecuencia. Estos resultados refuerzan la conclusión de que los errores del amplificador de retroalimentación se reducen por las grandes transmisiones de bucle y las frecuencias de ganancia unitaria.
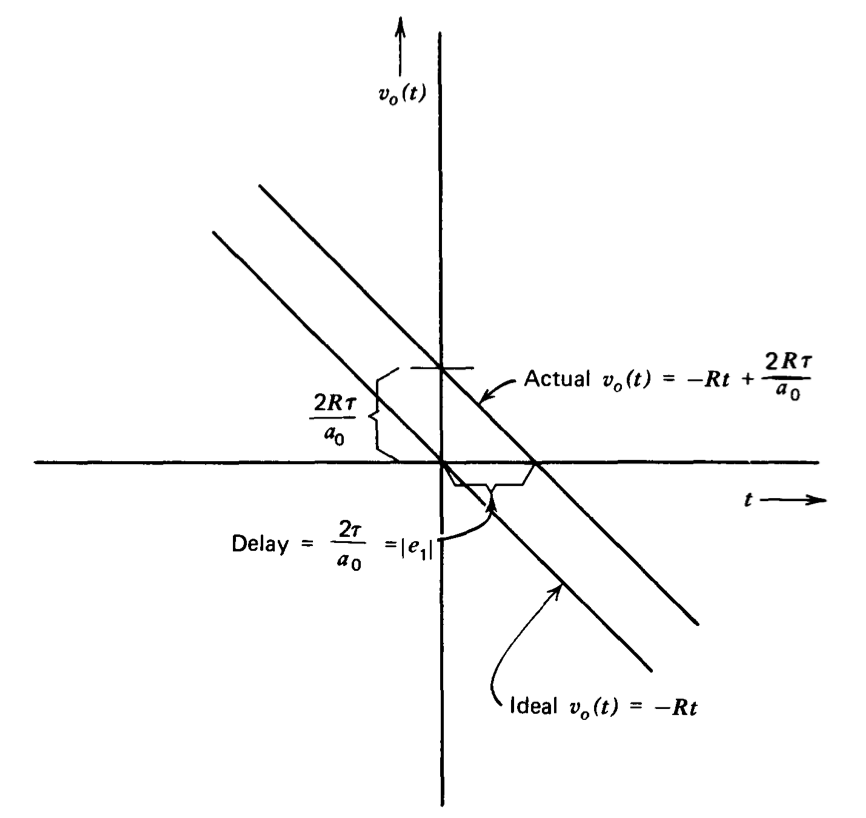
Si este amplificador está excitado con una rampa\(v_i (t) = Rt\), el error después de que se haya extinguido cualquier transitorio de arranque es
\[v_e (t) = e_0 v_i (t) + e_1 \dfrac{dv_i (t)}{dt} + \cdots + = -\dfrac{2Rt}{a_0} - \dfrac{2R\tau}{a_0} \nonumber \]
Debido a que el nivel máximo de señal de entrada está limitado por consideraciones de linealidad, (la tensión\(Rt\) debe ser menor que la tensión a la que se satura el amplificador) el segundo término de la serie de errores domina frecuentemente, y en estos casos el error es
\[v_e (t) \simeq - \dfrac{2R \tau}{a_0} \nonumber \]
lo que implica que la respuesta de rampa real del amplificador se queda por detrás de la salida ideal en una cantidad igual a la pendiente de la rampa dividida por la frecuencia de transmisión de bucle unitario. La respuesta en rampa del amplificador, asumiendo que la serie de errores está dominada por el\(e_1\) término, se compara con la respuesta en rampa de un sistema que utiliza un amplificador de ganancia infinita en la Figura 3.20. El error de rampa en estado estacionario, introducido anteriormente en las Ecuaciones 3.5.5 y 3.5.11 e ilustrado en la Figura 3.17\(c\), es evidente en esta figura.
Una observación adicional permite conocer el funcionamiento de este tipo de sistemas. Si las magnitudes relativas de la señal de entrada y sus derivadas están restringidas de manera que dominen los términos de primer orden (o superiores) en la serie de errores, la función de transferencia de bucle abierto del amplificador puede aproximarse como una integración.
\[a(s) \simeq \dfrac{a_0}{\tau s} \nonumber \]
Para que la salida de un amplificador con este tipo de ganancia de bucle abierto sea una rampa, es necesario tener una señal de error constante aplicada a la entrada del amplificador.
Seguir esta línea de razonamiento muestra aún más cómo se debe elegir la función de transferencia de bucle abierto del amplificador para reducir el error de rampa. El error se reduce claramente si\(a_0/\tau\) se aumenta la cantidad, pero tal aumento requiere un aumento correspondiente en la frecuencia de ganancia de unidad-bucle-ganancia. Desafortunadamente, las oscilaciones resultan para frecuencias de ganancia de unidad suficientemente altas. Alternativamente, considere el resultado si la función de transferencia de bucle abierto del amplificador se aproxima a una doble integración
\[a(s) \simeq \dfrac{a_0 (\tau s + 1)}{s^2} \nonumber \]
(El cero es necesario para asegurar la estabilidad. Véase Capítulo 4.) El lector debe verificar que ambos\(e_0\) y\(e_1\) son cero para un amplificador con esta función de transferencia de bucle abierto, lo que implica que el error de rampa de estado estacionario es cero. La manipulación adicional muestra que si la función de transferencia de bucle abierto del amplificador incluye una integración de orden n, los coeficientes de error\(e_0\) a través\(e_{n - 1}\) son cero.
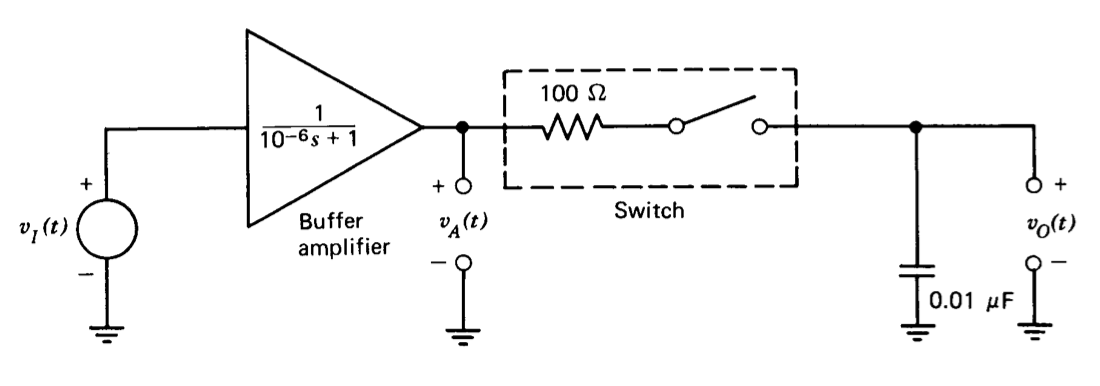
El uso de coeficientes de error para analizar sistemas excitados por señales de pulso se ilustra con la ayuda del circuito de muestreo y retención mostrado en la Figura 3.21. Este circuito consiste en un amplificador de búfer seguido de un interruptor y condensador. En la práctica, el interruptor se realiza frecuentemente con un transistor de efecto de campo, y la resistencia 100-9 modela la resistencia on del transistor. Cuando el interruptor está cerrado, el condensador se carga hacia el voltaje\(v_I\) a través de la resistencia del interruptor. Si el interruptor se abre a la vez\(t_A\), el voltaje idealmente\(v_O(t)\) debería mantener el valor\(v_I(t_A)\) para todos los tiempos mayor que\(t_A\). El amplificador de búfer se incluye para que la corriente de carga del condensador sea suministrada por el amplificador en lugar de por la fuente de señal. A menudo se incluye un segundo amplificador de búfer después del condensador para aislarlo de las cargas, pero este segundo amplificador no se requiere para el presente ejemplo.
Hay una variedad de efectos que degradan el rendimiento de un circuito de muestreo y retención. Una fuente importante de error deriva del hecho de que generalmente no\(v_O (t)\) es igual a\(v_I (t)\) menos\(v_I (t)\) que sea invariable en el tiempo debido a la dinámica del amplificador de búfer y la combinación de conmutador-condensador. Por lo tanto, se mantiene un valor incorrecto cuando se abre el interruptor.
Los coeficientes de error se pueden utilizar para predecir la magnitud de este error de seguimiento en función de la señal de entrada y la dinámica del sistema. A efectos de ilustración, se supone que el amplificador de búfer tiene una función de transferencia unipolar tal que
\[\dfrac{V_a (s)}{V_i (s)} = \dfrac{1}{10^{-6} s + 1} \nonumber \]
Dado que la constante de tiempo asociada con la combinación de conmutador-condensador es también de 1\(\mu\) s, la función de transferencia de entrada a salida con el interruptor cerrado (en cuyo caso el sistema es lineal, invariable en el tiempo) es
\[\dfrac{V_o (s)}{V_i (s)} = \dfrac{1}{(10^{-6} s + 1)^2} \nonumber \]
Con el interruptor cerrado, la salida es idealmente igual a la entrada y, por lo tanto, la función de transferencia de entrada a error es
\[\dfrac{V_e (s)}{V_i (s)} = 1 - \dfrac{V_o (s)}{V_i (s)} = \dfrac{10^{-12} s^2 + 2 \times 10^{-6} s}{(10^{-6} s + 1)^2}\label{eq3.6.17} \]
Los tres primeros coeficientes de error asociados a la Ecuación\(\ref{eq3.6.17}\), obtenidos por medio de división sintética, son
\[\begin{array} {rcl} {e_0} & = & {0} \\ {e_1} & = & {2 \times 10^{-6} \text{sec}} \\ {e_2} & = & {-3 \times 10^{-12} \text{sec}^2} \end{array} \nonumber \]
Los circuitos de muestreo y retención se utilizan frecuentemente para procesar pulsos como los echos de radar después de que estas señales hayan pasado a través de varias etapas de amplificador. En muchos casos el pulso después de la amplificación puede aproximarse bien por una señal gaussiana, y por esta razón una señal
\[v_i (t) = e^{-(10^{10} t^2/2)} \nonumber \]
se utiliza como entrada de prueba.
Los dos primeros derivados de\(v_i (t)\) son
\[\dfrac{dv_i (t)}{dt} = -10^{10} te^{-(10^{10} t^2/2)} \nonumber \]
y
\[\dfrac{d^2 v_i (t)}{dt^2} = -10^{10} e^{-(10^{10} t^2/2)} + 10^{20} t^2 e^{-(10^{10} t^2/2)} \nonumber \]
La magnitud máxima de\(dv_i/dt\) es\(6.07 \times 10^4\) voltios por segundo que ocurren en\(t = \pm 10^{-5}\) segundos, y la magnitud máxima de\(d^2 v_i/dt^2\) es\(10^{10}\) voltios por segundo al cuadrado en\(t = 0\). Si se utiliza el primer coeficiente de error para estimar el error, encontramos que se predice un error de seguimiento de aproximadamente 0.12 voltios (12% de la amplitud de la señal pico) si el interruptor se abre en\(t = \pm 10^{-5}\) segundos. La serie de errores converge rápidamente en este caso, con su segundo término contribuyendo con un error máximo de 0.03 voltios a\(t = 0\).
PROBLEMAS
Ejercicio\(\PageIndex{1}\)
Un amplificador operacional está conectado para proporcionar una ganancia no inversora de 10. La respuesta de paso de señal pequeña de la conexión es aproximadamente de primer orden con un 0 a 63% de tiempo de subida de 1\(\mu\) s. Estime la cantidad\(a(s)\) para el amplificador, asumiendo que la carga en la entrada y salida del amplificador es insignificante.
Ejercicio\(\PageIndex{2}\)
La función de transferencia de un sistema lineal es
\[A(s) = \dfrac{1}{(s^2 + 0.5s + 1)(0.1s + 1)} \nonumber \]
Determinar la respuesta escalonada de este sistema. Estimar (no calcular exactamente) el porcentaje de sobreimpulso de este sistema en respuesta a la excitación escalonada.
Ejercicio\(\PageIndex{3}\)
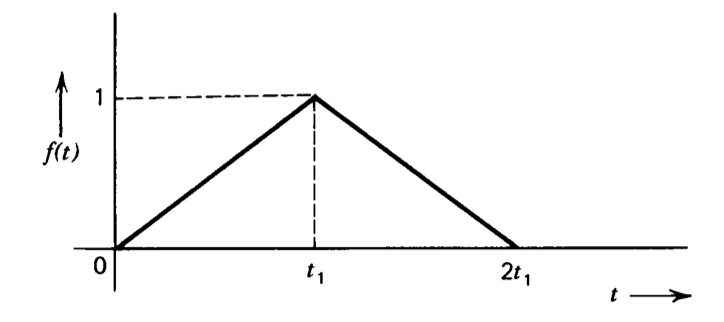
Utilice las propiedades de las transformaciones de Laplace para evaluar la transformación de la señal de pulso triangular mostrada en la Figura 3.22.
Ejercicio\(\PageIndex{4}\)
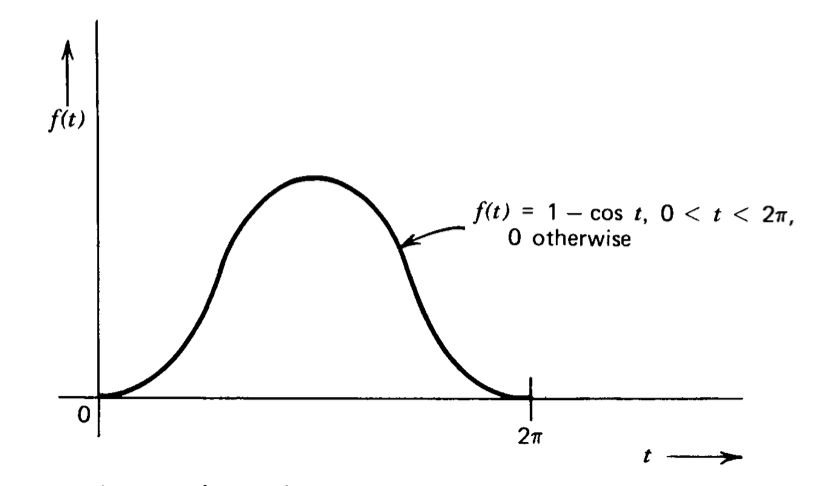
Utilice las propiedades de las transformaciones de Laplace para evaluar la transformación de la señal de pulso mostrada en la Figura 3.23.
Ejercicio\(\PageIndex{5}\)
La respuesta de cierto sistema lineal es aproximadamente de segundo orden, con una ganancia d-c de uno. El desempeño medido muestra que el valor máximo de la respuesta a un paso unitario es 1.38 y que el tiempo para que la respuesta del paso pase por uno primero es 0.5\(\mu\) s. Determine los parámetros de segundo orden que se pueden usar para modelar el sistema. También estime el valor pico de la salida que resulta cuando se aplica un impulso unitario a la entrada del sistema tem y el tiempo requerido para que la respuesta de impulso del sistema vuelva primero a cero. Estimar las cantidades\(M_p\) y\(f_h\) para este sistema.
Ejercicio\(\PageIndex{6}\)
Un amplificador de audio de alta fidelidad tiene una función de transferencia
\[A(s) = \dfrac{100s}{(0.05s + 1) (s^2/4 \times 10^{10} + s/2 \times 10^5 + 1)(0.5 \times 10^{-6} s + 1)} \nonumber \]
Trazar esta función de transferencia tanto en forma de Bode como de fase de ganancia. Reconozca que las singularidades de alta y baja frecuencia de este amplificador están ampliamente espaciadas y utilice este hecho para estimar las siguientes cantidades cuando el amplificador se excita con un paso de 10 mV.
(a) El valor pico de la señal de salida.
b) El momento en que se produce el valor pico.
c) El tiempo requerido para que la salida pase de 2 a 18 V. d
) El tiempo hasta que la salida baje a 7.4 V.
Ejercicio\(\PageIndex{7}\)
Un amplificador vertical de osciloscopio se puede modelar como teniendo una función de transferencia igual a\(A_0/(10^{-9}s + 1)^5\). Estime el tiempo de aumento de 10 a 90% de la tensión de salida cuando el amplificador se excita con una señal de entrada escalonada.
Ejercicio\(\PageIndex{8}\)
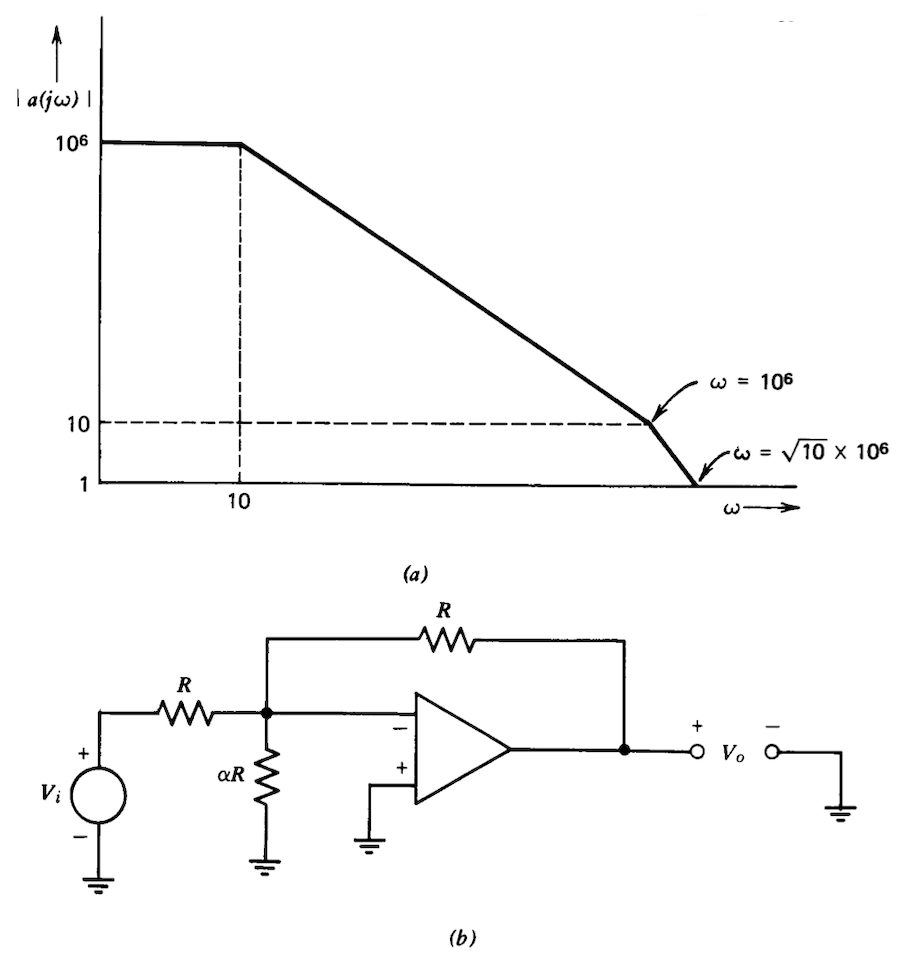
En la Figura 3.24 se muestra una gráfica asintótica de la respuesta de frecuencia de bucle abierto medida de un amplificador operacional\(a\). El amplificador está conectado como se muestra en la Figura 3.24\(b\). (Puede descuidar la carga.) Mostrar que los valores más bajos de un resultado en respuestas más fuertemente amortiguadas. Determinar el valor de a que da como resultado la respuesta escalonada de bucle cerrado del amplificador que tiene un sobreimpulso de 20% del valor final. ¿Cuál es el tiempo de subida del 10 al 90% en respuesta a un paso para este valor de\(\alpha\)?
Ejercicio\(\PageIndex{9}\)
Un sistema de retroalimentación tiene una ganancia hacia adelante\(a(s) = K/s(\tau s + 1)\) y una ganancia de retroalimentación\(f = 1\). Determinar las condiciones en\(K\) y\(\tau\) para que\(e_0\) y\(e_2\) sean ambos cero. ¿Cuál es el error de estado estacionario en respuesta a una rampa de unidad para este sistema?
Ejercicio\(\PageIndex{10}\)
Un amplificador operacional conectado como amplificador no inversor de ganancia unitaria se excita con una señal de entrada
\[v_i (t) = 5 \tan^{-1} 10^5 t\nonumber \]
Estimar el error entre las salidas reales e ideales asumiendo que la función de transferencia de bucle abierto puede aproximarse como se indica a continuación. (Tenga en cuenta que todas estas funciones de transferencia tienen valores idénticos para la frecuencia de ganancia unitaria).
(a)\(a(s) = 10^7 /s\)
b)\(a(s) = 10^{13} (10^{-6} s + 1)/s^2\)
c)\(a(s) = 10^{19} (10^{-6} s + 1)^2 /s^3\)
Ejercicio\(\PageIndex{11}\)
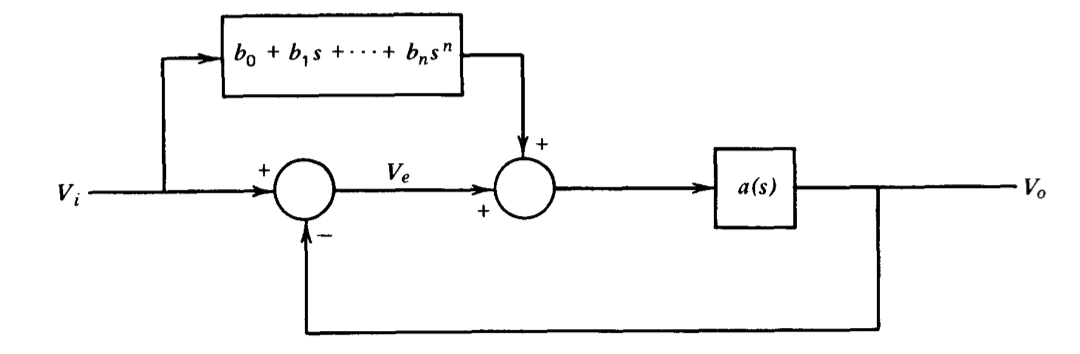
El sistema que se muestra en la Figura 3.25 utiliza una ruta de alimentación directa para reducir los errores. ¿Cómo se deben elegir los\(b\)'s para reducir los coeficientes de error\(e_0\)\(e_n\) a cero? ¿Se te ocurre alguna desventaja práctica de este esquema?