4.1: PROBLEMA DE ESTABILIDAD
- Page ID
- 84107
La discusión sobre los sistemas de retroalimentación presentados hasta este punto ha asumido tácitamente que los sistemas en estudio eran estables. Un sistema estable se define en general como aquel que produce una salida acotada en respuesta a cualquier entrada acotada. Así, la estabilidad implica que
\[\int_{-\infty}^{\infty} |v_O (t)| dt \le M < \infty \label{eq4.1.1} \]
para cualquier entrada tal que
\[\int_{-\infty}^{\infty} |v_I (t)| dt \le N < \infty \nonumber \]
Si limitamos nuestra consideración a los sistemas lineales, la estabilidad es independiente de la señal de entrada, y la condición suficiente y necesaria para la estabilidad es que todos los polos de la función de transferencia del sistema se encuentren en la mitad izquierda del plano s. Esta condición se deriva directamente de la Ecuación\(\ref{eq4.1.1}\), ya que cualquier polo de medio plano derecho aporta términos a la salida que crecen exponencialmente con el tiempo y por lo tanto no tienen límites. Obsérvese que esta definición implica que un sistema con polos en el eje imaginario es inestable, ya que su salida no está acotada a menos que su entrada sea elegida con bastante cuidado.
El origen del problema de estabilidad se puede describir de manera intuitiva y atractiva a través de términos no rigurosos de la siguiente manera. Si un sistema de retroalimentación detecta un error entre las salidas reales y deseadas, intenta reducir este error a cero. Sin embargo, los cambios en la señal de error que resultan de una acción correctiva no ocurren instantáneamente debido a los retardos de tiempo alrededor del bucle. En un sistema de alta ganancia, estos retrasos pueden provocar una tendencia a corregir en exceso. Si la magnitud de la sobrecorrección excede la magnitud del error inicial, resulta inestabilidad. Las amplitudes de la señal crecen exponencialmente hasta que cierta no linealidad limita el crecimiento adicional, momento en el que el sistema se satura u oscila de una manera de amplitud constante llamada ciclo límite. (El efecto de las no linealidades sobre la amplitud de estado estacionario alcanzada por un sistema inestable se investiga en el Capítulo 6.) El diseñador del sistema de retroalimentación siempre debe moderar su deseo de proporcionar una gran magnitud y una frecuencia de ganancia de unidad alta para la transmisión en bucle con el cierto conocimiento de que valores suficientemente altos para estas cantidades conducen invariablemente a la inestabilidad.
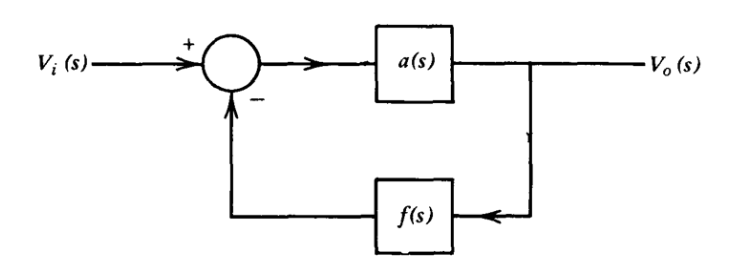
Como ejemplo específico de un sistema con comportamiento potencialmente inestable, considere un sistema simple de bucle único del tipo mostrado en la Figura 4.1, con
\[a(s) = \dfrac{a_0}{(s + 1)^3} \nonumber \]
y
\[f(s) = 1 \nonumber \]
La transmisión en bucle para este sistema es
\[-a(s) f(s) = \dfrac{-a_0}{(s + 1)^3} \nonumber \]
o para excitación sinusoidal,
\[-a(j\omega) f(j\omega) = \dfrac{-a_0}{(j \omega + 1)^3} = \dfrac{-a_0}{-j \omega^3 - 3 \omega^2 + 3j \omega + 1} \label{eq4.1.6} \]
Si evaluamos Ecuación\(\ref{eq4.1.6}\) en\(\omega = \sqrt{3}\), encontramos que
\[-a (j \sqrt{3}) f(j \sqrt{3}) = \dfrac{a_0}{8} \nonumber \]
Si la cantidad\(a_0\) se elige igual a 8, el sistema tiene una transmisión de bucle real y positivo con una magnitud de uno para excitación sinusoidal a tres radianes por segundo.
Podríamos sospechar que un sistema con una transmisión en bucle de +1 es capaz de oscilar, y este sospechoso puede confirmarse examinando la función de transferencia de bucle cerrado del sistema con\(a_0 = 8\). En este caso,
\[A(s) = \dfrac{a(s)}{1 + a(s) f(s)} = \dfrac{8}{s^3 + 3s^2 + 3s + 9} = \dfrac{8}{(s + 3) (s + j \sqrt{3}) (s - j\sqrt{3})} \nonumber \]
Esta función de transferencia tiene un polo negativo de eje real y un par de polos ubicados en el eje imaginario en\(s = \pm j \sqrt{3}\). Un argumento basado en las propiedades de las expansiones de fracción parcial (ver Sección 3.2.2) muestra que la respuesta de este sistema a muchas señales transitorias comunes (delimitadas) incluye una componente sinusoidal de amplitud constante.
Los aumentos adicionales en la magnitud de transmisión de bucle de baja frecuencia mueven el par de polos hacia el plano de la mitad derecha. Por ejemplo, si combinamos la función de transferencia de ruta directa
\[a(s) = \dfrac{64}{(s + 1)^3} \nonumber \]
con retroalimentación unitaria, la función de transferencia de bucle cerrado resultante es
\[A(s) = \dfrac{64}{s^3 + 3s^2 + 3s + 65} = \dfrac{64}{(s + 5) (s - 1 + j 2\sqrt{3})(s - 1 - j2\sqrt{3})} \nonumber \]
Con este valor para\(a_0\), la respuesta transitoria del sistema incluirá una componente sinusoidal con una envolvente en crecimiento exponencial.
Si la dinámica asociada a la transmisión en bucle permanece fija, el sistema será estable solo para valores\(a_0\) menores a 8. Esta estabilidad se logra a expensas de la desensitividad. Si se\(a_0 = 1\) usa un valor de para que
\[a(s) f(s) = \dfrac{1}{(s + 1)^3} \nonumber \]
encontramos que todos los polos de bucle cerrado están en el plano de la mitad izquierda, ya que
\[A(s) = \dfrac{1}{s^3 + 3s^2 + 3s + 2} = \dfrac{1}{(s + 2) (s + 0.5 + j \sqrt{3}/2) (s + 0.5 - j \sqrt{3}/2)} \nonumber \]
en este caso.
En ciertos casos limitados, una respuesta binaria a la pregunta de estabilidad es suficiente. Normalmente, sin embargo, nos interesará más información cuantitativa sobre el “grado” de estabilidad de un sistema de retroalimentación. Las medidas de estabilidad relativa utilizadas con frecuencia incluyen la magnitud máxima de la respuesta de frecuencia, el sobreimpulso fraccional en respuesta a una entrada escalonada, la relación de amortiguación asociada con el par de polos dominantes, o la variación de un determinado parámetro que puede tolerarse sin causar inestabilidad absoluta. Cualquiera de las medidas de estabilidad relativa mencionadas anteriormente se puede encontrar mediante cálculos directos que involucran la función de transferencia del sistema. Si bien tales determinaciones son prácticas con la ayuda del cálculo de la máquina, la comprensión del funcionamiento del sistema se oscurece con frecuencia si se usa este proceso. Las técnicas descritas en este capítulo tienen como objetivo no sólo dar respuesta a preguntas sobre estabilidad, sino también (y más importante) para indicar cómo mejorar el rendimiento de los sistemas de fábrica unsatis.


