4.3: TÉCNICAS DE LOCUS DE
- Page ID
- 84103
Un amplificador de retroalimentación de bucle único se muestra en el diagrama de bloques de la Figura 4.1. La función de transferencia de bucle cerrado para este amplificador es
\[\dfrac{V_0 (s)}{V_i (s)} = A(s) = \dfrac{a(s)}{1 + a(s) f(s)} \nonumber \]
Las técnicas de locus raíz proporcionan un método para encontrar los polos de la función de transferencia de bucle cerrado\(A(s)\) [o equivalentemente los ceros de\(1 + a(s)f(s)\)] dados los polos y ceros de\(a(s)f(s)\) y la magnitud de transmisión de bucle d-c\(a_0 f_0\). (Si la transmisión en bucle tiene uno o más ceros en el origen para que su magnitud d-c sea cero, los polos de bucle cerrado se encuentran a partir del valor de banda media de\(af\).) Observe que dado que la cantidad\(a_0 f_0\) debe aparecer en uno o más términos de la ecuación característica, las ubicaciones de los polos de\(A(s)\) deben depender de\(a_0f_0\). Un diagrama raíz-locus consiste en una colección de ramas o loci en el plano s que indican cómo\(a_0f_0\) varían las ubicaciones de los polos de\(A(s)\) cambio.
El diagrama de locus raíz proporciona información útil sobre el rendimiento de un sistema de retroalimentación, ya que la estabilidad relativa de cualquier sistema lineal está determinada únicamente por sus ubicaciones de polos de bucle cerrado. Encontraremos que los diagramas aproximados de locus raíz se esbozan fácil y rápidamente, y que proporcionan una visión fácilmente interpretada sobre cómo el rendimiento de bucle cerrado de un sistema responde a los cambios en su transmisión en bucle. También veremos que las técnicas de locus raíz se pueden combinar con métodos algebraicos simples para dar respuestas exactas en ciertos casos.
Formando el diagrama
Un ejemplo simple que ilustra varias características importantes de las técnicas de locus raíz es proporcionado por el sistema mostrado en la Figura 4.1 con una función de transferencia de retroalimentación\(f\) de unidad y una función de transferencia directa.
\[a(s) = \dfrac{a_0}{(\tau_a s + 1)(\tau_b s + 1)} \nonumber \]
La función de transferencia de bucle cerrado correspondiente es
\[A(s) = \dfrac{a(s)}{1 + a(s) f(s)} = \dfrac{a_0}{\tau_a \tau_b s^2 + (\tau_a + \tau_b) s + (1 + a_0)} \nonumber \]
Los polos de bucle cerrado se pueden determinar factorizando la ecuación característica de\(A(s)\), rindiendo
\[s_1 = \dfrac{-(\tau_a + \tau_b) + \sqrt{(\tau_a + \tau_b)^2 - 4 (1 + a_0) \tau_a \tau_b}}{2 \tau_a \tau_b}\label{eq4.3.4} \]
\[s_2 = \dfrac{-(\tau_a + \tau_b) - \sqrt{(\tau_a + \tau_b)^2 - 4 (1 + a_0) \tau_a \tau_b}}{2 \tau_a \tau_b}\label{eq4.3.5} \]
El diagrama raíz-locus en la Figura 4.3 se dibuja con la ayuda de la Ecuación\(\ref{eq4.3.4}\) y\(\ref{eq4.3.5}\). Entre las características importantes de este diagrama se incluyen las siguientes.

(a) Se muestran las ubicaciones de los polos de transmisión en bucle. (Los ceros de transmisión de bucle también se indican si están presentes).
(b) Los polos de\(A(s)\) coinciden con los polos de transmisión en bucle para\(a_0 = 0\).
c) A medida que aumenta ao, las ubicaciones de los polos de\(A(s)\) cambio a lo largo de los loci como se muestra. Las flechas indican la dirección de los cambios que resultan para aumentar\(a_0\).
Los dos polos coinciden en la media aritmética de las ubicaciones de los polos de la misión loop-trans para el radical cero en la Ecuación\(\ref{eq4.3.4}\) y\(\ref{eq4.3.5}\), o para
\[a_0 = \dfrac{(\tau_a + \tau_b)^2}{4 \tau_a \tau_b} - 1 \label{eq4.3.6} \]
(e) Para aumentos en ao más allá del valor de la Ecuación\(\ref{eq4.3.6}\), el par de polos de bucle cerrado es complejo con parte real constante y una relación de amortiguación que es una función decreciente monotónica de\(a_0\). En consecuencia,\(\omega_0\) aumenta con el pliegue\(a_0\) en este rango.
Ciertas características importantes del comportamiento del sistema son evidentes a partir del diagrama. Por ejemplo, el sistema no se vuelve inestable por ningún valor positivo de ao. Sin embargo, la estabilidad relativa disminuye a medida que ao aumenta más allá del valor indicado en la Ecuación\(\ref{eq4.3.6}\).
Siempre es posible dibujar un diagrama root-locus factorizando directamente la ecuación característica del sistema en estudio como en el ejemplo anterior. Desafortunadamente, el esfuerzo involucrado en la factorización de polinomios de orden superior hace que el cálculo de la máquina sea obligatorio para todos, excepto para los sistemas más simples. Veremos que es posible aproximar los diagramas de locus raíz y así conservar el conocimiento que a menudo se pierde con el cálculo de la máquina cuando no se requiere precisión absoluta.
La clave para desarrollar las reglas utilizadas para aproximar los loci es darse cuenta de que los polos de bucle cerrado ocurren solo a ceros de la ecuación característica o a frecuencias\(s_1\) tales que (Se supone a lo largo de todo que el sistema en estudio es un sistema de retroalimentación negativa con la topología mostrada en la Figura 4.1)
\[1 + a(s_1) f(s_1) = 0 \nonumber \]
o
\[a(s_1) f(s_1) = -1 \nonumber \]
Por lo tanto, si el punto\(s_1\) es un punto en una rama del diagrama raíz-locus, las dos condiciones
\[|a(s_1) f (s_1)|= -1\label{eq4.3.9} \]
y
\[\measuredangle a(s_1) f(s_1) = (2n + 1) 180^{\circ}\label{eq4.3.10} \]
donde\(n\) es cualquier entero, debe ser satisfecho. La condición de ángulo es la más importante de estas dos restricciones con el propósito de formar un diagrama de ubicación raíz. La razón es que ya que trazamos los loci como\(a_0f_0\) es variado, es posible encontrar un valor para a\(a_0f_0\) que satisfaga la condición de magnitud en cualquier punto del\(s\) plano donde se satisfaga la condición de ángulo.
Al concentrarnos principalmente en la condición de ángulo, podemos formu tarde un conjunto de reglas que simplifican enormemente la construcción del diagrama de raíz, locus en comparación con la factorización de fuerza bruta de la ecuación característica. Estas son algunas de las reglas que usaremos.
1. El número de ramas del diagrama es igual al número de polos de\(a(s)f(s)\). Cada rama comienza en un polo de\(a(s)f(s)\) para valores pequeños de\(a_0f_0\) y se acerca a un cero de\(a(s)f(s)\) ya sea en el plano s finito o en el infinito para valores grandes de\(a_0f_0\). Los puntos de inicio y finalización se demuestran considerando
\[a(s) f(s) = a_0 f_0 g(s) \nonumber \]
donde\(g(s)\) contiene la porción dependiente de la frecuencia de la transmisión de bucle y el valor de\(g(0) \triangleq g_0\) es unidad. Reorganización de la ecuación\(\ref{eq4.3.9}\),\(\ref{eq4.3.10}\) y el uso de esta notación rinde
\[|g(s_1)| = \dfrac{1}{a_0 f_0} \nonumber \]
en cualquier punto\(s_1\) de una rama del diagrama raíz-locus. Así para valores pequeños de\(a_0f_0\),\(|g(s_1)|\) debe ser grande, lo que implica que el punto si está cerca de un polo de\(g(s)\). Por el contrario, un gran valor de\(a_0f_0\) requiere proximidad a un cero de\(g(s)\).
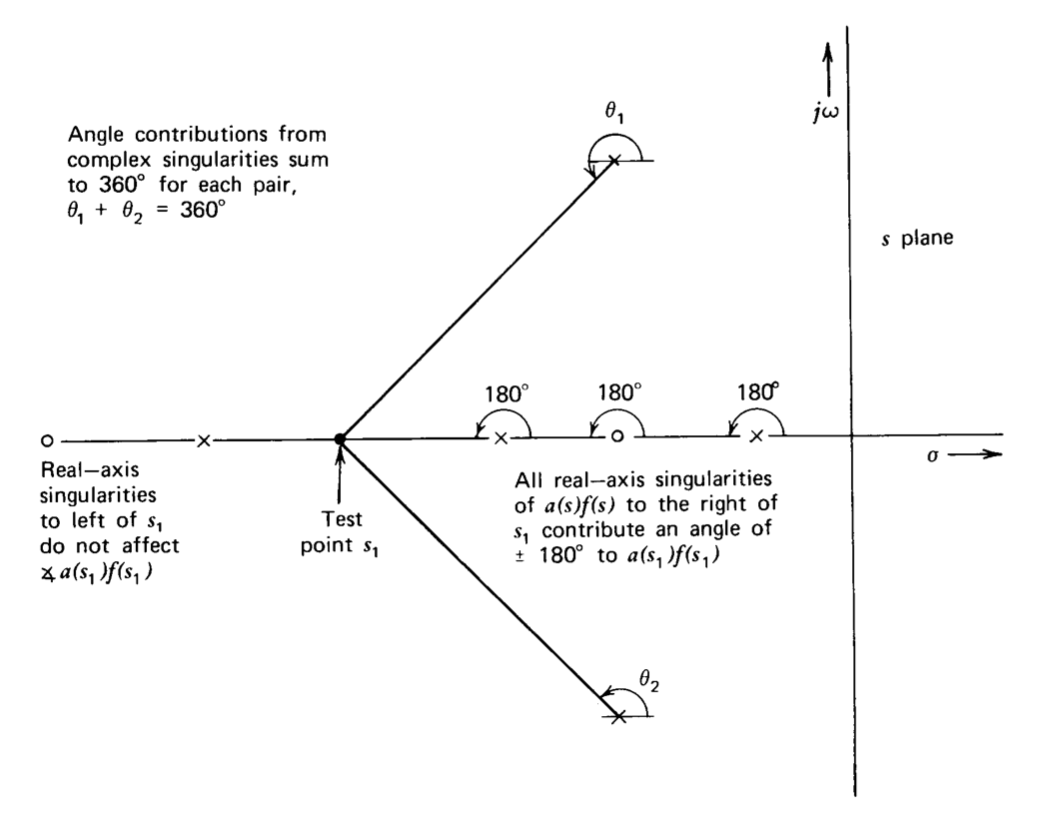
2. Las ramas del diagrama se encuentran en el eje real a la izquierda de un número impar de polos de eje real y ceros de\(a(s)f(s)\). (Es necesario tener especial cuidado en sistemas con singularidades de bucle abierto de medio plano derecho. Ver Sección 4.3.3.) Esta regla sigue directamente de la Ecuación\(\ref{eq4.3.10}\) como se ilustra en la Figura 4.4. Cada cero de eje real\(a(s)f(s)\) a la derecha de se\(s_1\) suma\(180^{\circ}\) al ángulo de\(a(s_1)f(s_1)\) mientras que cada polo de eje real a la derecha\(180^{\circ}\) de\(s_1\) resta del ángulo. Las singularidades del eje real a la izquierda del punto\(s_1\) no influyen en el ángulo de\(a(s_1)f(s_1)\). Del mismo modo, dado que las singularidades complejas deben ocurrir siempre en pares conjugados, la contribución del ángulo neto de estas singularidades es cero. Esta regla es así suficiente para satisfacer la Ecuación\(\ref{eq4.3.10}\). Se nos garantiza además que las ramas deben existir en todos los segmentos del eje real a la izquierda de un número impar de singularidades de\(a(s)f(s)\), ya que hay algún valor de\(a_0f_0\) que satisfará exactamente Ecuación\(\ref{eq4.3.9}\) en cada punto de estos segmentos, y la satisfacción de Ecuaciones \(\ref{eq4.3.9}\)y\(\ref{eq4.3.10}\) es a la vez necesario y suficiente para la existencia de un polo de\(A(s)\).
3. Las dos ramas separadas del diagrama que deben existir entre pares de polos o pares de ceros en segmentos del eje real que satisfagan la regla 2 deben en algún momento apartarse o entrar en el eje real en ángulo recto con él. Con frecuencia, no se requiere el punto de ruptura preciso para esbozar los loci con una precisión aceptable. Si es necesario tener una ubicación exacta, se puede demostrar que los puntos de ruptura son las soluciones de la ecuación
\[\dfrac{d[g(s)]}{ds} = 0\label{eq4.3.13} \]
para sistemas sin singularidades coincidentes.
4. Si el número de polos de\(a(s)f(s)\) excede el número de ceros de esta función en dos o más, la distancia promedio de los polos de\(A(s)\) desde el eje imaginario es independiente de\(a_0f_0\). Esta regla evoluciona a partir de una propiedad de polinomios algebraicos. Considerar un polinomio
\[\begin{array} {rcl} {P(s)} & = & {(a_1 s + a_1 s_1) (a_2 s + a_2 s_2) (a_3 s + a_3 s_3) \cdots (a_n s + a_n s_n)} \\ {} & = & {(a_1 a_2 \cdots a_n) (s + s_1) (s + s_2) (s + s_3) \cdots (s + s_n)} \\ {} & = & {(a_1 a_2 \cdots a_n) [s^n + (s_1 + s_2 + s_3 + \cdots + s_n) s^{n - 1} + \cdots + s_1 s_2 s_3 \cdots s_n]} \end{array}\label{eq4.3.14} \]
A partir de la expresión final de Ecuación\(\ref{eq4.3.14}\), vemos que la relación de los coeficientes del\(s^{n-1}\) término y el término sn (denotado como\(-n\bar{s}\)) es
\[-n \bar{n} = s_1 + s_2 + s_3 \cdots + s_n\label{eq4.3.15} \]
Dado que los componentes imaginarios de términos en el lado derecho de la Ecuación\(\ref{eq4.3.15}\) deben ocurrir en pares conjugados y así cancelar, la cantidad
\[s = -\dfrac{(s_1 + s_2 + s_3 + \cdots + s_n)}{n}\label{eq4.3.16} \]
es la distancia promedio de las raíces\(P(s)\) del eje imaginario. Para aplicar la ecuación\(\ref{eq4.3.16}\) a la ecuación característica de un sistema de retroalimentación, supongamos que
\[a(s) f(s) = a_0 f_0 \dfrac{p(s)}{q(s)} \nonumber \]
Entonces
\[A(s) = \dfrac{a(s)}{1 + a(s) f(s)} = \dfrac{a(s)}{1 + a_0 f_0 [p(s)/q(s)]} = \dfrac{a(s)q(s)}{q(s) + a_0 f_0 p(s)} \nonumber \]
Si el orden de\(q(s)\) excede el de\(p(s)\) en dos o más, la relación de los coeficientes de los dos términos de orden superior de la ecuación característica de\(A(s)\) es independiente de\(a_0f_0\), y así la distancia promedio de los polos de\(A(s)\) desde el eje imaginario es una constante.
5. Para grandes valores de\(a_0f_0\), las\(P - Z\) ramas se acercan al infinito, donde\(P\) y\(Z\) son el número de polos y ceros de plano finito de\(a(s)f(s)\), respectivamente. Estas ramas se acercan a asíntotas que hacen ángulos con el eje real dado por
\[\theta_n = \dfrac{(2n + 1) 180^{\circ}}{P - Z}\label{eq4.3.19} \]
En Ecuación\(\ref{eq4.3.19}\),\(n\) asume todos los valores enteros de 0 a\(P - Z - 1\). Todas las asíntotas se cruzan con el eje real en un punto
\[\dfrac{\sum \text{ real parts of poles of } a(s) f(s) - \sum \text{ real parts of zeros of } a(s) f(s)}{P - Z} \nonumber \]
La prueba de esta regla se deja al Problema P4.4.
6. Cerca de un polo complejo de\(a(s)f(s)\), el ángulo de una rama con respecto al polo es
\[\theta_p = 180^{\circ} + \sum \measuredangle z - \sum \measuredangle p \nonumber \]
donde\(\sum \measuredangle z\) está la suma de los ángulos de vectores dibujados de todos los ceros del\(a(s)f(s)\) polo complejo en cuestión y\(\sum \measuredangle p\) es la suma de los ángulos de vectores dibujados de todos los demás polos del\(a(s)f(s)\) polo complejo. Del mismo modo, el ángulo que hace una rama con un bucle de transmisión cero en las proximidades del cero es
\[\theta_z = 180^{\circ} - \sum \measuredangle z + \sum \measuredangle p \nonumber \]
Estas condiciones siguen directamente de la Ecuación\(\ref{eq4.3.10}\).

7. Si las singularidades de\(a(s)f(s)\) incluyen un grupo mucho más cercano al origen que todas las demás singularidades de\(a(s)f(s)\), las singularidades de mayor frecuencia pueden ignorarse a la hora de determinar loci en las proximidades del origen. La figura 4.5 ilustra esta situación. Se supone que el punto si está en una rama si se ignoran las singularidades de alta frecuencia, y así el ángulo de la porción de baja frecuencia de\(a(s)f(s)\) evaluada en\(s = s_1\) debe ser\((2n + 1)\ 180^{\circ}\). La geometría muestra que la contribución angular atribuible a singularidades remotas como la indicada como\(\theta_1\) es pequeña. (Los dos ángulos de un par complejo-conjugado remoto también se suman a un ángulo pequeño). Pequeños cambios en la ubicación de\(s_1\) eso pueden causar cambios relativamente grandes en el ángulo (e.g.,\(\theta_2\)) de las singularidades de baja frecuencia compensan la contribución de las singularidades remotas, lo que implica que ignorar las singularidades remotas da como resultado cambios significativos en el diagrama raíz-locus en la cercanía de las singularidades de baja frecuencia. Además, todas las ubicaciones de polos de bucle cerrado estarán relativamente cerca de sus puntos de partida para valores bajos y moderados de\(a_0f_0\). Dado que la discusión de la Sección 3.3.2 muestra que\(A(s)\) estará dominada por sus polos de menor frecuencia, las singularidades de mayor frecuencia de\(a(s)f(s)\) pueden ignorarse cuando nos interesa el desempeño del sistema para valores bajos y moderados de\(a_0f_0\).
8. El valor de\(a_0f_0\) requerido para hacer que un polo de bucle cerrado se encuentre\(s_1\) en el punto de una rama del diagrama de locus raíz es
\[a_0 f_0 = \dfrac{1}{|g(s_1)|}\label{eq4.3.22} \]
donde\(g(s)\) se define en la regla 1. Esta regla es necesaria para satisfacer la Ecuación\(\ref{eq4.3.9}\).
Ejemplos
El diagrama de locus raíz que se muestra en la Figura 4.3 se puede desarrollar usando las reglas dadas anteriormente en lugar de factorizar el denominador de la función de transferencia de bucle cerrado. El comportamiento general de las dos ramas en el eje real se determina utilizando las reglas 2 y 3. Si bien el punto de ruptura se puede encontrar en la ecuación\(\ref{eq4.3.13}\), es más fácil usar la regla 4 o la regla 5 para
establecer el comportamiento fuera del eje. Dado que la distancia promedio de los polos de bucle cerrado desde el eje imaginario debe permanecer constante para este sistema [el número de polos de\(a(s)f(s)\) es dos mayor que el número de sus ceros], las ramas deben moverse paralelas al eje imaginario después de que abandonen el eje real. Además, la distancia promedio debe ser idéntica a la de\(a_0f_0 = 0\), y así el segmento paralelo al eje imaginario debe ubicarse en\(-\tfrac{1}{2} [(1/\tau_a) + (1/\tau_b)]\). La regla 5 da el mismo resultado, ya que muestra que las dos ramas deben acercarse a asíntotas verticales que se cruzan con el eje real en\(-\tfrac{1}{2} [(1/\tau_a) + (1/\tau_b)]\).
Los diagramas de locus raíz más interesantes resultan para sistemas con más singularidades de transmisión de bucle. Por ejemplo, la función de transferencia de un amplificador con tres etapas de emisor común normalmente tiene tres polos a frecuencias moderadas y tres polos adicionales a frecuencias considerablemente más altas. La regla 7 indica que los tres polos de alta frecuencia pueden ignorarse si este tipo de amplificador se usa en una conexión de retroalimentación con valores moderados de transmisión de bucle d-c. Si se asume que la retroalimentación negativa independiente de la frecuencia se aplica alrededor del amplificador de tres etapas, un producto af representativo podría ser (Las ubicaciones de los polos correspondientes en - 1, -2, y\(-10\ \text{sec}^{-1}\) son irrealistas bajas para la mayoría de los amplificadores. Estos valores resultan, sin embargo, si la función de transferencia para un amplificador con polos en\(- 10^6\)\(- 2 X 10^6\), y\(- 10^7 \text{sec}^{-1}\) se normaliza usando el microsegundo en lugar del segundo como la unidad de tiempo básica. Dicho escalado de frecuencia se utilizará a menudo ya que elimina algunos de los poderes difíciles de manejar de 10 de nuestros cálculos).
\[a(s) f(s) = \dfrac{a_0 f_0}{(s + 1)(0.5s + 1)(0.1s + 1)} \nonumber \]
El diagrama raíz-locus para este sistema se muestra en la Figura 4.6. La regla 2 determina el diagrama sobre el eje real, mientras que la regla 5 establece las asíntotas. La regla 4 se puede utilizar para estimar las ramas fuera del eje real, ya que las ramas correspondientes a los dos polos de menor frecuencia deben moverse hacia la derecha para equilibrar la rama que va a la izquierda desde el polo de alta frecuencia. El punto de ruptura se puede determinar a partir de la ecuación\(\ref{eq4.3.13}\), con
\[\dfrac{d[g(s)]}{ds} = \dfrac{-[0.15 s^2 + 1.3 s + 1.6]}{[(s + 1) (0.5s + 1) (0.1 s + 1)]^2}\label{eq4.3.24} \]
Los ceros de la ecuación\(\ref{eq4.3.24}\) están en\(- 7.2 \text{sec}^{-1}\) y\(- 1.47 \text{sec}^{-1}\). La ubicación de frecuencia más alta no tiene sentido para este problema, y de hecho corresponde a un punto de ruptura que resulta si se aplica retroalimentación positiva alrededor del amplificador. Tenga en cuenta que el punto de ruptura se puede estimar con precisión usando la regla 7. Si se ignora el polo de frecuencia relativamente más alta en,\(10 \text{sec}^{-1}\) se\(- 1.5 \text{sec}^{-1}\) produce un punto de ruptura para la función de transferencia bipolar restante.
Las manipulaciones algebraicas pueden ser utilizadas para obtener más información cuantitativa sobre el sistema. La Figura 4.6 muestra que el sistema se vuelve no estable a medida que dos polos se mueven hacia el plano de la mitad derecha para valores suficientemente grandes de\(a_0f_0\). El valor de\(a_0f_0\) que mueve el par de polos de bucle cerrado sobre el eje imaginario se encuentra aplicando el criterio de Routh a la ecuación característica del sistema, que es (después de borrar fracciones)
\[\begin{array} {rcl} {P(s)} & = & {(s + 1) (0.5s + 1) (0.1s + 1) + a_0 f_0} \\ {} & = & {0.05s^3 + 0.65 s^2 + 1.6s + 1 + a_0 f_0} \end{array}\label{eq4.3.25} \]
La matriz Routh es
\[\begin{array} {cc} {0.05} & {1.6} \\ {0.65} & {1 + a_0 f_0} \\ {\dfrac{1}{0.65} (0.99 - 0.05 a_0 f_0)} & {0} \\ {1 + a_0 f_0} & {0} \end{array} \nonumber \]
Se producen dos inversiones de signos que indican inestabilidad para\(a_0 f_0 > 19.8\). Con este valor de\(a_0 f_0\), la ecuación auxiliar es
\[Q(s) = 0.65 s^2 + 20.8 \nonumber \]
Las raíces de esta ecuación indican que los polos cruzan el eje imaginario en\(s = \pm j (5.65)\).

También es posible determinar valores para\(a_0f_0\) ese resultado en configuraciones de polos de bucle cerrado especificadas. Este tipo de cálculo se ilustra encontrando el valor de\(a_0f_0\) requerido para proporcionar una relación de amortiguación de 0.5, correspondiente a polos de par complejo ubicados\(60^{\circ}\) desde el eje real. La magnitud de la relación de la parte imaginaria a la parte real de la ubicación del polo para un par de polos con\(\zeta = 0.5\) es\(\sqrt{3}\). Así, la ecuación característica para este sistema, cuando la relación de amortiguación del par de polos complejos es 0.5, es
\[\begin{array} {rcl} {P'(s)} & = & {(s + \gamma )(s + \beta + j \sqrt{3} \beta )(s + \beta - j \sqrt{3} \beta } \\ {} & = & {s^3 + (\gamma + 2\beta )s^2 + 2\beta (\gamma + 2\beta ) s + 4 \gamma \beta^2} \end{array} \nonumber \]
donde\(-\gamma\) está la ubicación del polo del eje real.
Los parámetros se determinan multiplicando la Ecuación\(\ref{eq4.3.25}\) por 20 (para hacer el coeficiente del\(s^3\) término unidad) e igualando la nueva ecuación a\(P' (s)\).
\[s^3 + 13s^2 + 32 s + 20 (1 + a_0 f_0) = s^3 + (\gamma + 2\beta) s^2 + 2\beta (\gamma + 2\beta )s + 4 \gamma \beta^2\label{eq4.3.29} \]
\(\ref{eq4.3.29}\)La ecuación se resuelve fácilmente para\(\gamma , \beta\), y\(a_0f_0\), con los resultados
Varias características del sistema son evidentes a partir de este análisis. Dado que el par complejo se encuentra en el\(s = -1.23 (1 \pm j \sqrt{3})\) momento en el que se encuentra el polo del eje real\(s = - 10.54\), una aproximación de dos polos basada en el par debe modelar con precisión la respuesta transitoria o de frecuencia del sistema. La desensitividad relativamente baja\(1 + a_0f_0 = 3.2\) resulta si la relación de amortiguación del par complejo se hace 0.5, y cualquier aumento en la desensitividad dará como resultado una amortiguación más pobre. El análisis anterior muestra que los intentos de incrementar la desensitividad más allá de 20.8 resultan en inestabilidad.
Tenga en cuenta que dado que en nuestros cálculos solo existía un grado de libertad (el valor de\(a_0f_0\)), solo se pudo controlar una característica del patrón de polos de bucle cerrado. No es posible forzar valores arbitrarios para más de una de las tres cantidades que definen las ubicaciones de los polos de bucle cerrado (\(\zeta\)y\(\omega_n\), para el par y la ubicación del polo real) a menos que se permitan más grados de libertad de diseño.
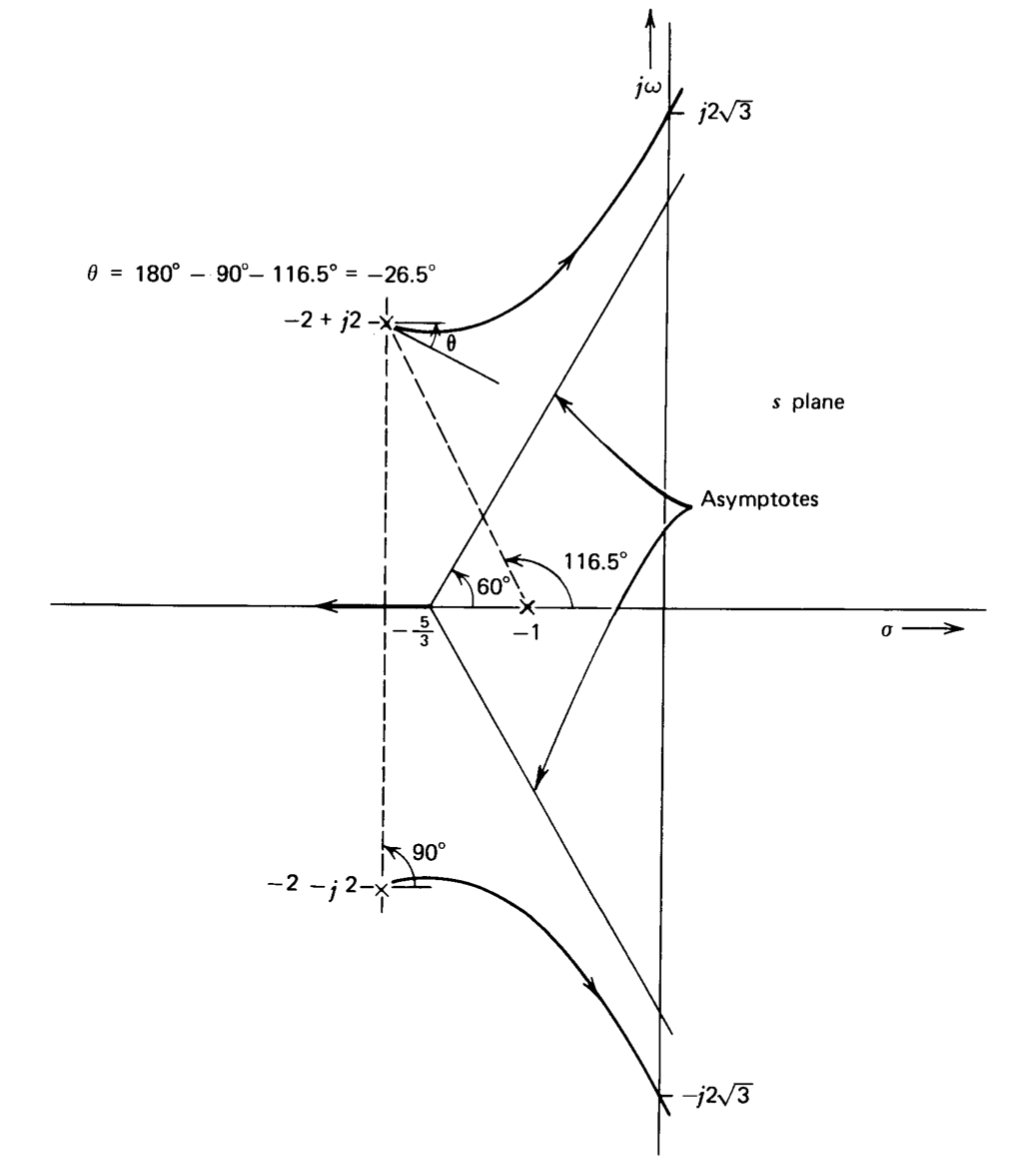
Otro ejemplo de construcción de diagrama radical-locus se muestra en la Figura 4.7, el diagrama para
\[a(s) f(s) = \dfrac{a_0 f_0}{(s + 1)(s^2/8 + s/2 + 1)} \nonumber \]
La regla 5 establece las asíntotas, mientras que la regla 6 se utiliza para determinar los loci cercanos a los polos complejos. El valor\(a_0f_0\) para el cual el par complejo de polos entra en el plano de la mitad derecha y la frecuencia a la que cruzan el eje imaginario se encuentran según el criterio de Routh. El lector debe verificar que estos polos cruzan el eje imaginario en\(s = \pm j 2 \sqrt{3}\) for\(a_0 f_0 = 6.5\).
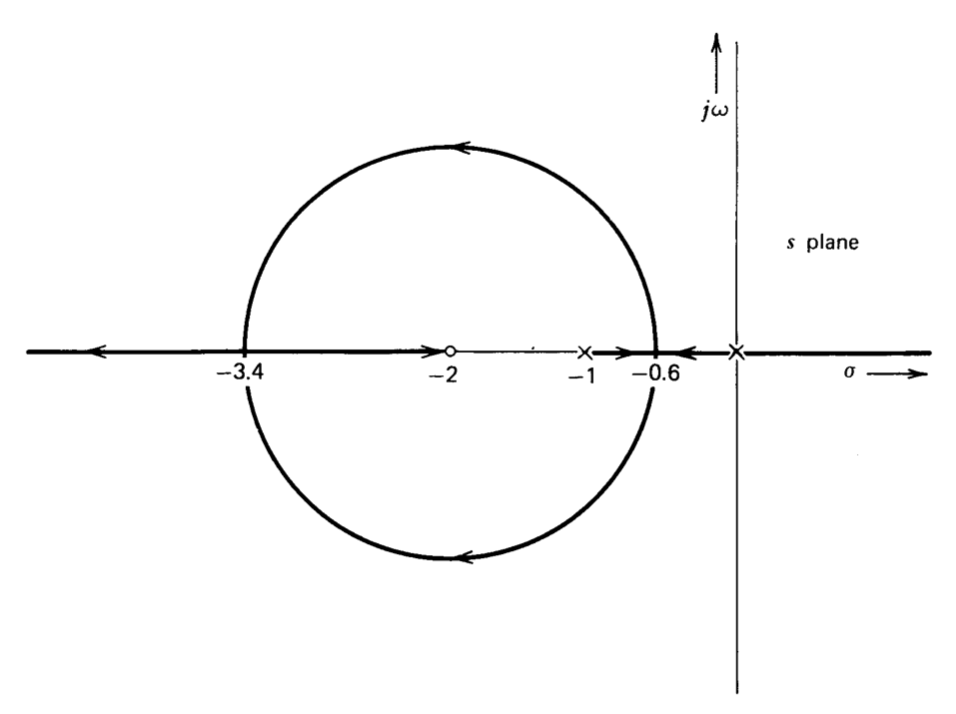
El diagrama de locus raíz para un sistema con
\[a(s) f(s) = \dfrac{a_0 f_0 (0.5s + 1)}{s (s + 1)} \nonumber \]
se muestra en la Figura 4.8. La regla 2 indica que las ramas están en el eje real entre los dos polos de transmisión de bucle y a la izquierda del cero. Los puntos de salida y reingreso al eje real se obtienen resolviendo
\[\dfrac{d}{ds} \left [ \dfrac{(0.5s + 1)}{(s (s + 1)} \right] = 0 \nonumber \]
cediendo\(s = -2 \pm \sqrt{2}\).
Sistemas con singularidades de transmisión en bucle de medio plano derecho
Es necesario tener especial cuidado con el signo de la transmisión de bucle cuando se dibujan diagramas de locus raíz para sistemas con singularidades de transmisión de bucle de medio plano derecho. Algunos sistemas que son inestables sin retroalimentación tienen uno o más polos de transmisión de bucle en el plano de la mitad derecha. Por ejemplo, un cohete grande no se vuelve aerodinámicamente estable hasta que alcanza cierta velocidad crítica, y volcaría poco después del despegue si el empuje no fuera vectorizado por medio de un sistema de retroalimentación. Se puede demostrar que la función de transferencia del cohete por sí sola incluye un polo de medio plano derecho de eje real.
Un ejemplo más familiar surge de un amplificador de emisor común de una sola etapa. La función de transferencia de este tipo de amplificador incluye un polo a frecuencia moderada, un segundo polo a alta frecuencia y un cero de semiplano derecho de alta frecuencia que refleja la señal alimentada hacia adelante de entrada a salida a través de la capacitancia colector a base del transistor. Un producto af representativo para este tipo de amplificador con retroalimentación independiente de la frecuencia aplicada a su alrededor es
\[a(s) f(s) = \dfrac{a_0 f_0 (-10^{-3} s + 1)}{(10^{-3} s + 1) (s + 1)}\label{eq4.3.34} \]
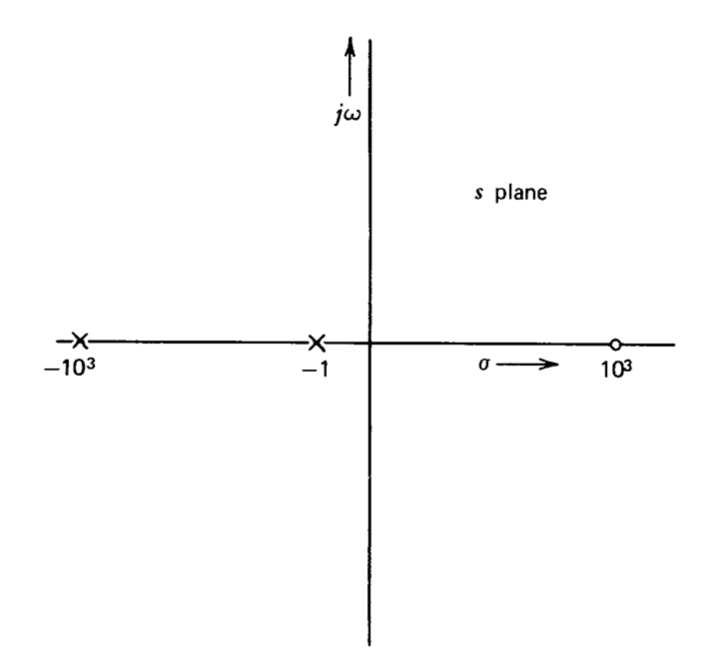
Las singularidades para este amplificador se muestran en la Figura 4.9. Si las reglas de locus raíz se aplican ciegamente, concluimos que el polo de baja frecuencia se mueve hacia la derecha y entra en el plano medio derecho para magnitudes de transmisión de bucle d-c superiores a una. Afortunadamente, la evidencia experimental refuta este resultado. La dificultad proviene del signo de la ganancia de baja frecuencia. Se ha asumido a lo largo de esta discusión que la transmisión en bucle es negativa a baja frecuencia para que el sistema tenga retroalimentación negativa. Las reglas se desarrollaron asumiendo la topología mostrada en la Figura 4.1 donde la retroalimentación negativa da como resultado cuándo\(a_0\) y\(f_0\) tienen el mismo signo. Si consideramos los sistemas de retroalimentación positiva, la ecuación\(\ref{eq4.3.10}\) debe cambiarse a
\[\measuredangle a(s_1) f(s_1) = n 360^{\circ} \label{eq4.3.35} \]
donde\(n\) es cualquier entero, y las reglas evolucionadas a partir de la condición de ángulo deben modificarse apropiadamente. Por ejemplo, la regla 2 se cambia a “las ramas se encuentran en el eje real a la izquierda de un número par de singularidades del eje real para los sistemas de retroalimentación positiva”.
El patrón de singularidad mostrado en la Figura 4.9 corresponde a una función de transferencia
\[a'(s) f' (s) = \dfrac{a_0 f_0 (10^{-3}s - 1}{(10^{-3} s + 1)(s + 1)} = \dfrac{-a_0 f_0 (-10^{-3} s + 1)}{(10^{-3} s + 1)(s + 1)} \nonumber \]
porque el vector desde el cero a\(s = 0\) tiene un ángulo de\(180^{\circ}\). La inversión de signo asociada con el cero cuando se grafica en el diagrama\(s\) plano ha cambiado el signo de la transmisión del bucle d-c en comparación con el de la Ecuación\(\ref{eq4.3.34}\). Una forma de revertir los efectos de este cambio de signo es sustituir Ecuación\(\ref{eq4.3.35}\) por Ecuación\(\ref{eq4.3.10}\) y modificar todas las reglas dependientes del ángulo en consecuencia.
Una técnica mucho más simple que funciona igualmente bien para amplificadores con los ceros del plano de la mitad derecha ubicados a altas frecuencias es ignorar estos ceros al formar el diagrama de locus raíz. Dado que la eliminación de estos ceros elimina las inversiones de signos asociadas, no es necesaria ninguna modificación de las reglas. La regla 7 asegura que el diagrama no se cambie para magnitudes moderadas de transmisión en bucle ignorando los ceros de alta frecuencia.
Ubicación de Closed-Loop Zeros
Un diagrama de locus raíz indica la ubicación de los polos de bucle cerrado de un sistema de retroalimentación. Además de la información de estabilidad proporcionada por las ubicaciones de los polos, es posible que necesitemos las ubicaciones de los ceros de bucle cerrado para determinar algunos aspectos del rendimiento del sistema.
El método utilizado para determinar los ceros de bucle cerrado se desarrolla con la ayuda de la Figura 4.10. Parte\(a\) de esta figura muestra el diagrama de bloques para un sistema de retroalimentación de bucle único. El diagrama de la Figura 4.10\(b\) tiene la misma función de transferencia de entrada-salida que la de la Figura 4.10\(a\), pero se ha modificado para que la ruta de retroalimentación dentro del bucle tenga ganancia de unidad. Primero consideramos la función de transferencia de bucle cerrado
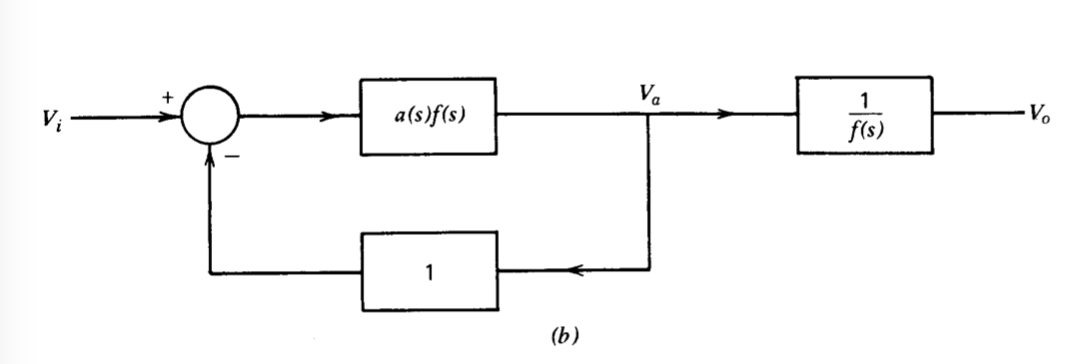
\[\dfrac{V_a (s)}{V_i (s)} = \dfrac{a(s) f(s)}{1 + a(s)f(s)}\label{eq4.3.37} \]
Un diagrama de locus raíz da las ubicaciones de los polos para esta función de transferencia de bucle cerrado directamente, ya que el diagrama indica las frecuencias a las que el denominador de la ecuación\(\ref{eq4.3.37}\) es cero. Los ceros de Ecuación\(\ref{eq4.3.37}\) coinciden con los ceros de la función de transferencia\(a(s)f(s)\). Sin embargo, a partir de la Figura\(b\) 4.10,
\[A(s) = \left [ \dfrac{V_o (s)}{V_i (s)} \right ] = \left [ \dfrac{V_a (s)}{V_i (s)} \right ] \left [ \dfrac{V_o (s)}{V_a (s)} \right ] = \left [ \dfrac{V_a (s)}{V_i (s)} \right ] \left [ \dfrac{1}{f(s)} \right ] \label{eq4.3.38} \]
Así, además de las singularidades asociadas con la Ecuación\(\ref{eq4.3.37}\),\(A(s)\) tiene polos en los polos de\(1/f(s)\), o equivalentemente en ceros de\(f(s)\), y tiene ceros en los polos de\(f(s)\). Los polos adicionales de Ecuación\(\ref{eq4.3.38}\) cancelan los ceros de\(f(s)\) en Ecuación\(\ref{eq4.3.37}\), con el resultado neto que\(A(s)\) tiene ceros en ceros de\(a(s)\) y en polos de\(f(s)\). Es importante reconocer que los ceros de\(A(s)\) son inde pendent de\(a_0f_0\).
Un enfoque alternativo es reconocer que los ceros de\(A(s)\) ocurren en ceros del numerador de esta función y en frecuencias donde el denominador se vuelve infinito mientras que el numerador permanece finito. La condición posterior se cumple en polos de\(f(s)\), ya que este término se incluye en el denominador de\(A(s)\) pero no en su numerador.
Tenga en cuenta que las singularidades de\(A(s)\) son particularmente fáciles de determinar si la ruta de retroalimentación es independiente de la frecuencia. En este caso, (como siempre) los polos de bucle cerrado se obtienen directamente del diagrama de locus raíz. Los ceros de\(a(s)\), que son los únicos ceros trazados en el diagrama cuando\(f(s) = f_0\), son también los ceros de\(A(s)\).
Estos conceptos se ilustran por medio de dos ejemplos de amplificadores de retroalimentación selectivos de frecuencia. Amplificadores de este tipo se pueden construir combinando\(T\) redes gemelas con amplificadores operacionales. Una\(T\) red doble puede tener una función de transferencia de voltaje que incluye ceros complejos con partes reales positivas, negativas o cero. Se supone que un gemelo\(T\) con una relación de transferencia de voltaje (La función de transferencia de una red Twin-T incluye un tercer cero de eje real, así como un tercer polo. Además, ninguno de los polos coincide. El alejamiento de la realidad representada por Ecuación\(\ref{eq4.3.39}\) simplifica el siguiente desarrollo sin cambiar significativamente las conclusiones. El lector que esté interesado en la función de transferencia de este tipo de redes es referido a J. E. Gibson y F. B. Tuteur, Control System Components, McGraw-Hill, Nueva York, 1958, Sección 1.26. )
\[T(s) = \dfrac{s^2 + 1}{s^2 + 2s + 1} \label{eq4.3.39} \]
está disponible.
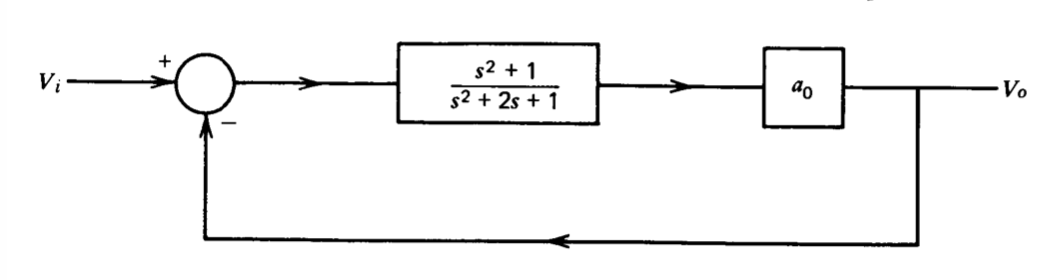
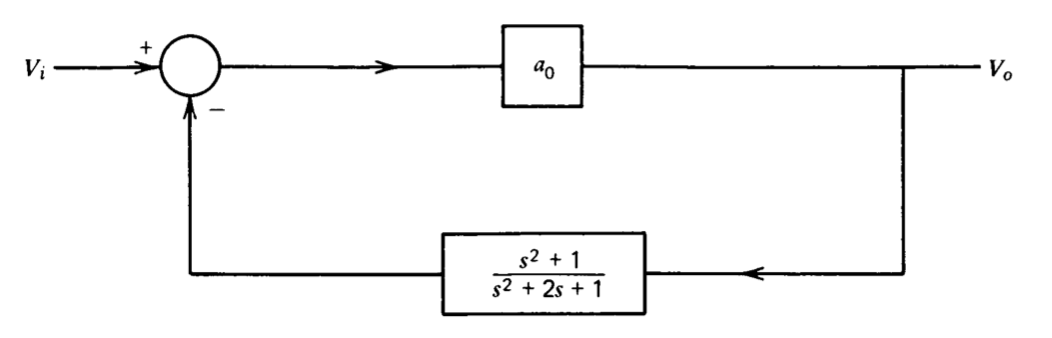
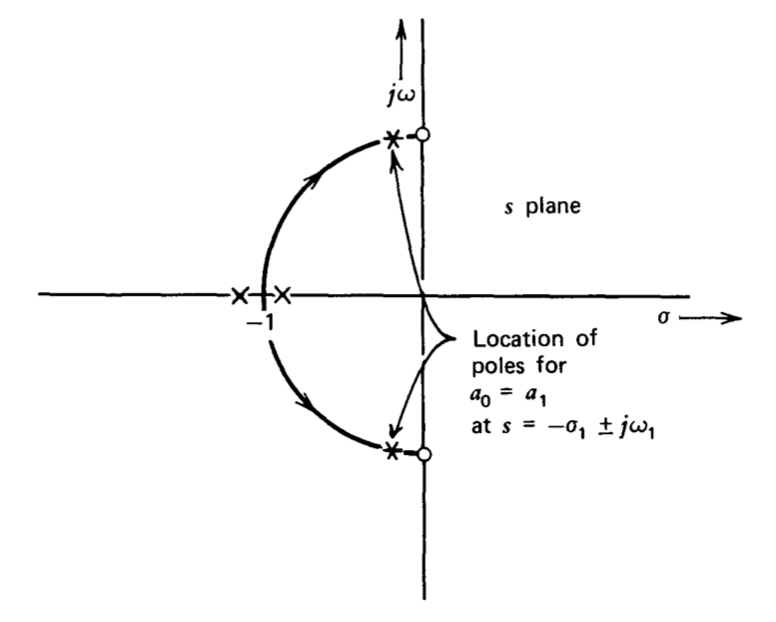
Las figuras 4.11 y 4.12 muestran dos formas de combinar esta red con un amplificador que se supone que tiene ganancia constante ao a frecuencias de interés. Dado que ambos sistemas tienen la misma transmisión de bucle, tienen diagramas de locus raíz idénticos como se muestra en la Figura 4.13. Los polos de bucle cerrado dejan el eje real para cualquier valor finito de ao y se acercan a los ceros\(j\) del eje a lo largo de arcos circulares. La ubicación del polo de bucle cerrado para un valor particular de ao también se indica en esta figura.
El amplificador de rechazo (Figura 4.11) se considera primero. Dado que la conexión tiene una ruta de retroalimentación independiente de la frecuencia, sus ceros de bucle cerrado son los dos que se muestran en el diagrama de locus raíz. Si la señal Vi es una sinusoide de amplitud constante, los efectos de los polos y ceros de bucle cerrado casi se cancelan excepto en frecuencias cercanas a un radián por segundo. La respuesta de frecuencia de bucle cerrado se indica en la Figura 4.14\(a\). A medida\(a_0\) que se incrementa, la distancia entre los polos de bucle cerrado y los ceros se vuelve más pequeña. Así, la banda de frecuencias sobre la cual los polos y ceros no cancelan se vuelve más estrecha, lo que implica una muesca más nítida, a medida que se incrementa ao.
El amplificador de paso de banda combina los polos del diagrama de locus raíz con un cero en bucle cerrado de segundo orden\(s = - 1\), correspondiente al par de polos de\(f(s)\). La función de transferencia de bucle cerrado no tiene otros ceros, ya que no\(a(s)\) tiene ceros en este sentido. La respuesta de frecuencia para este amplificador se muestra en la Figura 4.14\(b\). En este caso el amplificador se vuelve más selectivo y proporciona mayor ganancia a un radián por segundo a medida que aumenta ao, ya que la relación de amortiguación del par de polos complejos disminuye.
Contornos de raíz
El método root-locus nos permite determinar cómo cambian las ubicaciones de los polos de bucle cerrado de un sistema de retroalimentación a medida que se varía la magnitud de la transmisión de bucle de baja frecuencia. Hay muchos sistemas en los que se requiere estabilidad relativa en función de algún parámetro distinto a la ganancia. Veremos, por ejemplo, que la ubicación de una singularidad de bucle abierto en la función de transferencia de un amplificador operacional se varía frecuentemente para compensar el amplificador y así mejorar su rendimiento en una aplicación dada. Las técnicas de locus raíz podrían usarse para trazar una familia de diagramas de locus raíz correspondientes a varios valores para un parámetro del sistema que no sea ganancia. También es posible extender los conceptos de locus raíz para que la variación en la ubicación de los polos de bucle cerrado como una función de algún parámetro único que no sea ganancia se determine para un valor fijo de\(a_0f_0\). El diagrama de locus raíz generalizado que resulta de esta extensión se denomina diagrama de contorno de raíz.
Para ver cómo se construyen los contornos de raíz, recordamos que la ecuación característica para un sistema de retroalimentación negativa se puede escribir en la forma
\[P(s) = q(s) = a_0 f_0 p(s) \nonumber \]
donde se supone que
\[a(s) f(s) = a_0 f_0 \dfrac{p(s)}{q(s)} \nonumber \]

Si el\(a_0f_0\) producto es constante, pero algún otro parámetro del sistema\(\tau\) varía, la ecuación característica se puede reescribir
\[P(s) = q'(s) + \tau p'(s) \label{eq4.3.41} \]
Todos los términos que\(\tau\) se multiplican están incluidos\(p'(s)\) en la Ecuación\(\ref{eq4.3.41}\), de manera que\(q'(s)\) y ambos\(p'(s)\) son independientes de\(\tau\). El diagrama de contorno raíz como una función de entonces se\(\tau\) puede dibujar aplicando las reglas de construcción a un patrón de singularidad que tiene polos en ceros\(q'(s)\) y ceros en ceros de\(p'(s)\).
Un amplificador operacional conectado como seguidor de unidad-ganancia se utiliza para ilustrar la construcción de un diagrama de contorno de raíz. Esta conexión tiene retroalimentación unitaria, y se supone que la función de transferencia de bucle abierto del amplificador es
\[a(s) = \dfrac{10^6 (\tau s + 1)}{(s + 1)^2} \nonumber \]
La ecuación característica después de borrar fracciones es
\[P(s) = s^2 + 2s + (10^6 + 1) + \tau 10^6 s \nonumber \]
Identificar términos de acuerdo con\(\ref{eq4.3.41}\) los resultados de la Ecuación en
\[p' (s) = 10^6 s \nonumber \]
\[q' (s) = s^2 + 2s + 10^6 + 1 \simeq s^2 + 2s + 10^6 \nonumber \]
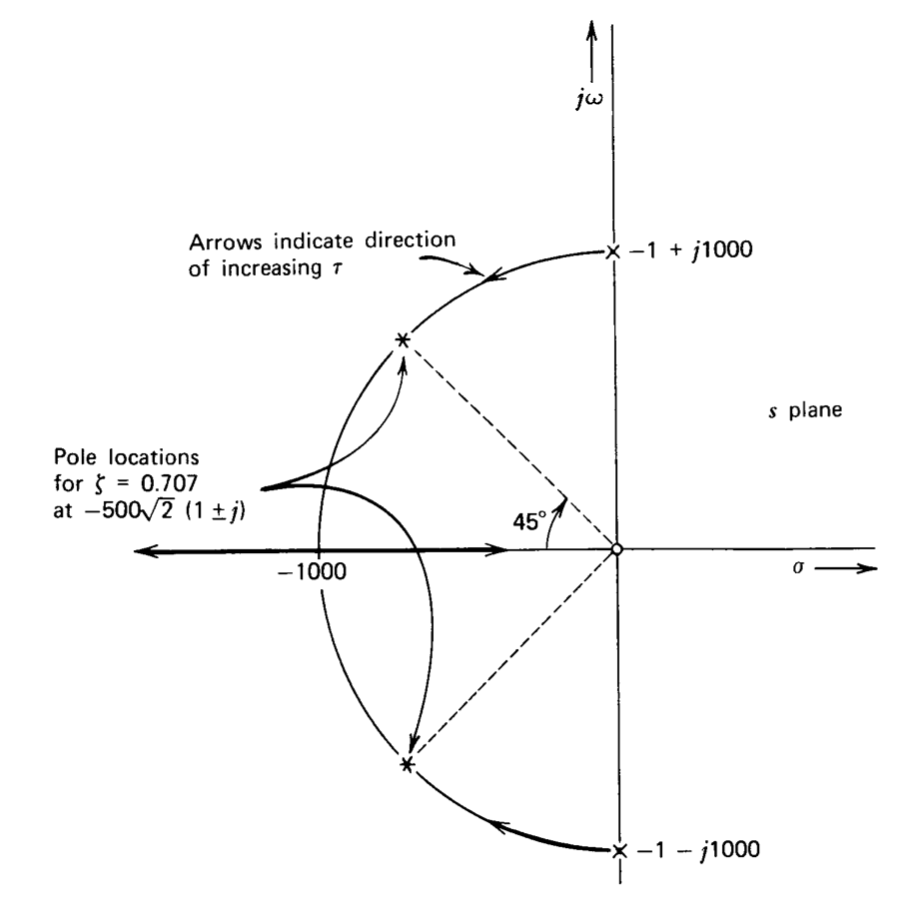
Así, el patrón de singularidad utilizado para formar los contornos de la raíz tiene un cero en el origen y polos complejos en\(s = - 1 \pm j 10^3\). El diagrama raíz-contorno se muestra en la Figura 4.15. La regla 8 se utiliza para encontrar el valor de\(\tau\) necesario para ubicar el par de polos complejos a\(45^{\circ}\) partir del eje real negativo correspondiente a una relación de amortiguación de 0.707. A partir de la ecuación\(\ref{eq4.3.22}\), el valor requerido es
\[\begin{array} {rcl} {\tau} & = & {\left |\dfrac{q'(s)}{p'(s)} \right |_{s = -500 \sqrt{2} (1 + j)}} \\ {} & = & {\left |\dfrac{s^2 + 2s + 10^6}{10^6 s} \right |_{s = -500 \sqrt{2} (1 + j)} = \sqrt{2} \times 10^{-3}} \end{array} \nonumber \]


