8.2: TOPOLOGÍAS AMPLIFICADORES
- Page ID
- 84124
Los requisitos generalmente limitan las etapas de entrada y salida de un amplificador operacional para que sean un amplificador diferencial y algún tipo de búfer (normalmente una conexión emisor-seguidor), respectivamente.
Es en la etapa intermedia o etapas donde la flexibilidad del diseño es evidente, y la diferencia en el rendimiento entre un circuito bueno y uno malo a menudo
refleja las diferencias en el diseño de la etapa intermedia. El objetivo principal de rendimiento es que esta parte del circuito proporcione ganancia de alto voltaje acoplada con una función de transferencia que permita un comportamiento estable de banda ancha en una variedad de conexiones de retroalimentación. Además, la flexibilidad de modificar fácil y predeciblemente la función de transferencia de bucle abierto del amplificador con el fin de optimizarla para una conexión de retroalimentación particular es deseable para un diseño de propósito general.
Diseño con tres etapas de ganancia de voltaje
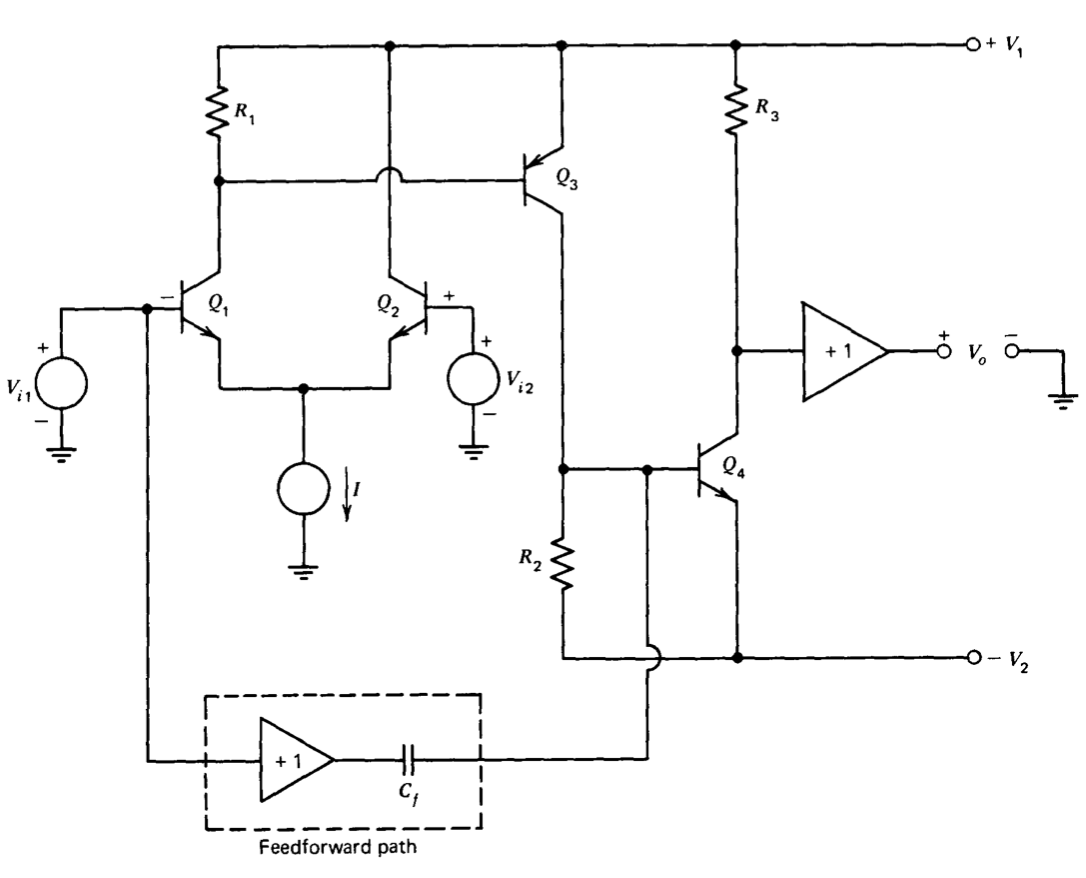
Un diseño de uso muy frecuente se muestra en forma simplificada en la Figura 8.1. La ruta etiquetada feedforward es una técnica utilizada para estabilizar el amplificador, y no es esencial para la descripción inicial de la operación. El
El circuito básico utiliza una entrada diferencial ya que esta conexión es obligatoria para baja deriva y alta relación de rechazo en modo común. Se utilizan dos etapas de emisor común (transistores\(Q_3\) y\(Q_4\)) para proporcionar la característica de ganancia de alto voltaje de los amplificadores operativos. Se utiliza algún tipo de amplificador de búfer (mostrado diagramáticamente como el amplificador de ganancia de unidad en la porción de salida) para proporcionar las características de salida requeridas.
La inspección casual indica algún mérito para el diseño de la Figura 8.1. Es posible una baja deriva y se pueden lograr ganancias d-c superiores a 10. La dificultad es evidente sólo cuando se examina la dinámica del amplificador. La función de transferencia\(V_o(s)/ [V_{i2} (s) - V_{i1} (s)]\) determina la estabilidad en las conexiones de retroalimentación. Con valores típicos de elementos, esta función de transferencia tiene tres o cuatro polos ubicados dentro de un rango de frecuencia de dos a tres décadas. No es posible lograr una gran magnitud de transmisión de bucle y simultáneamente mantener la estabilidad con este tipo de función de transferencia. Se debe desalentar al diseñador de este tipo de amplificadores cuando compare su circuito con el de un oscilador de desplazamiento de fase, donde se aplica retroalimentación negativa alrededor de tres o más polos estrechamente espaciados.
El problema puede ilustrarse calculando la función de transferencia para el amplificador que se muestra en la Figura 8.1 con los valores de los componentes enumerados en la Tabla 8.1. Las razones para seleccionar estos valores de componentes son las siguientes. Se utilizan suministros de quince voltios ya que este valor se ha convertido en el estándar para muchos amplificadores operativos de estado sólido. La corriente de funcionamiento en reposo de la primera etapa es baja para reducir la corriente de polarización de entrada.
Se utilizan aumentos relativamente modestos en las corrientes de reposo de etapa a etapa para minimizar los efectos de carga. En estos niveles, las impedancias del circuito son tales que se producen pocos cambios en la función de transferencia si\(r_x\) se asume igual a cero. Sin embargo, se\(r_x\) ha retenido para su completitud. Las capacitancias de unión están dominadas por efectos de capa de carga espacial a bajas rentas cur operativas, por lo que se han asumido valores iguales para todas las capacitancias de transistores. Claramente, cualquier cambio igual en todas las capacitancias simplemente escala la frecuencia de la función de transferencia. Las resistencias en los circuitos base de\(Q_3\) y\(Q_4\) se suponen grandes para maximizar la ganancia d-c. En la práctica, las fuentes de corriente se pueden utilizar para mantener una alta resistencia incremental y para establecer corrientes de polarización. \(R_3\)La resistencia se elige para producir un voltaje de salida quiescente igual a cero.
Cuadro 8.1. Valores de Parámetro para Ejemplo Usando Amplificador de la Figura 8.1
| Voltajes de alimentación: \(\pm 15\ V\) |
| Corrientes de polarización: \(I_{C1} = I_{C2} = 10\ \mu A\) \(I_{C3} = 50\ \mu A\) \(I_{C4} = 250\ \mu A\) |
| Transconductancia (1) implícita por las corrientes de polarización: \(g_{m1} = g_{m2} = 4 \times 10^{-4} \text{ mho}\) \(g_{m3} = 2 \times 10^{-3} \text{ mho}\) \(g_{m4} = 10^{-2} \text{ mho}\) (1) Recordemos que para cualquier transistor bipolar que funcione a niveles de corriente donde Las gotas óhmicas no son importantes, la transconductancia está relacionada con la corriente de colector quiescente por\(g_m = q|I_C|/kT \simeq 40 V^{-1} |I_C|\) a temperatura ambiente. |
| Otros parámetros del transistor: \(\beta = 100 \text{ (all transistors)}\) \(r_{\pi 1} = r_{\pi 2} = 250\ k\Omega\) \(r_{\pi 3} = 50\ k \Omega\) \(r_{\pi 4} = 10\ k \Omega\) \(r_{x} = 100 \Omega \text{ (all transistors)}\) \(C_{\mu} = C_{\pi} = 10\text{ pF (all transistors)}\) |
| Resistencias: \(R_1\) y\(R_2\) grandes comparadas con\(r_{\pi 3}\) y\(r_{\pi 4}\), respectivamente. \(R_3 = 60\ k\Omega\) (Satisfacer las desigualdades normalmente requiere que se utilicen fuentes de corriente en lugar de resistencias en diseños prácticos). Se supone que el amplificador de búfer tiene impedancia de entrada infinita. |
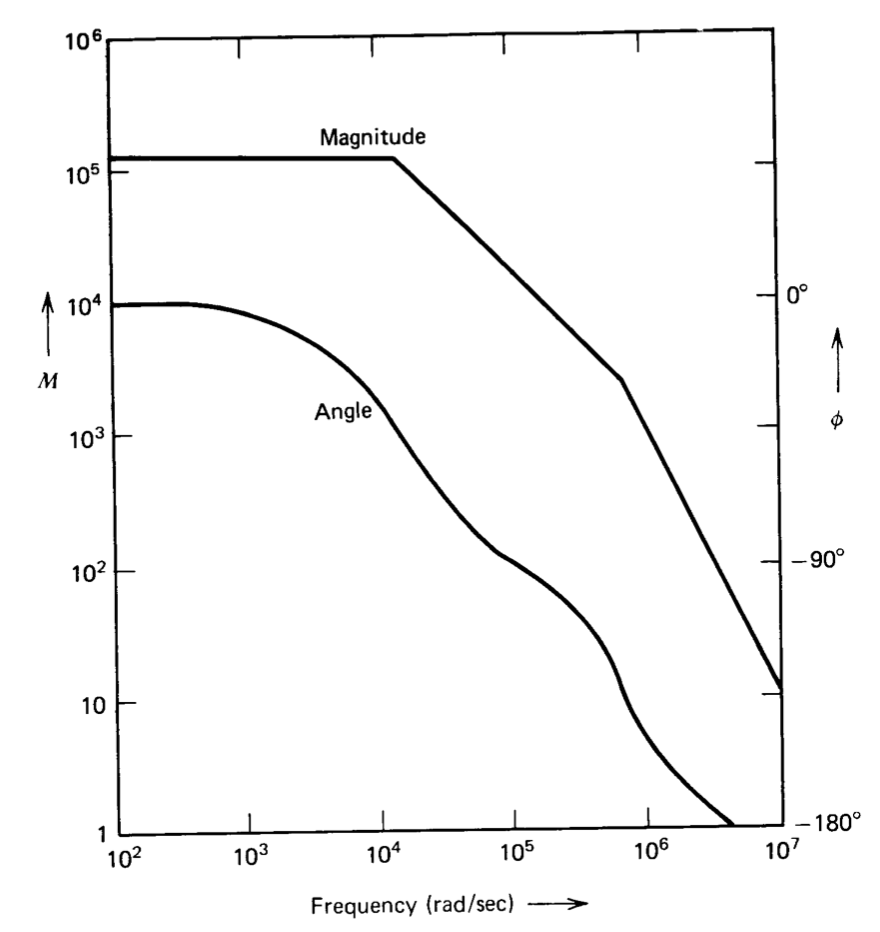
Una función de transferencia generada por computadora\(V_o (j\omega)/[V_{i2} (j\omega) - V_{i1} (j\omega)]\) para este amplificador se muestra en forma de diagrama de Bodes en la Figura 8.2. (Las ganancias del amplificador para las señales aplicadas a sus dos entradas no son idénticas a altas frecuencias debido a que una fracción de la señal aplicada a la base de\(Q_1\) se acopla directamente a la base de\(Q_3\) vía la capacitancia colector-a-base de\(Q_1\). Este efecto, que es insignificante hasta que las frecuencias se acercan a las\(f_T\)'s de los transistores utilizados en el circuito, se ha ignorado en el cálculo de la función de transferencia del amplificador para que resulte una verdadera expresión de ganancia diferencial). Dos características importantes de esta función de transferencia se relacionan fácilmente con los parámetros del circuito. La ganancia de baja frecuencia se puede determinar mediante inspección. Invocando los supuestos habituales, los cambios incrementales en la corriente del colector de primera etapa están relacionados con un cambio incremental en el voltaje de entrada diferencial como
\[i_{c1} = - \left (\dfrac{v_{i2} - v_{i1}}{1/g_{m1} + 1/g_{m2}} \right ) \label{eq8.2.1} \]
Dado que\(R_1\) es grande en comparación con la resistencia de entrada de\(Q_3\), toda esta corriente incremental fluye hacia la base de\(Q_3\). Esta corriente base se amplifica por un factor de\(\beta_3\), y la corriente incremental resultante fluye hacia la base de\(Q_4\). El voltaje de salida incremental se convierte
\[v_o = i_{c1} \beta_3 \beta_4 R_3 \label{eq8.2.2} \]
combinando ecuaciones\(\ref{eq8.2.1}\) y\(\ref{eq8.2.2}\) muestra que la ganancia de voltaje de baja frecuencia es
\[\dfrac{v_o}{v_{12} - v_{i1}} = \dfrac{\beta_3 \beta_4 R_3}{(1/g_{m1} + 1/g_{m2})} \nonumber \]
Sustituir los valores de los parámetros de la Tabla 8.1 en esta ecuación muestra que la ganancia incremental d-c es\(1.2 \times 10^5\).
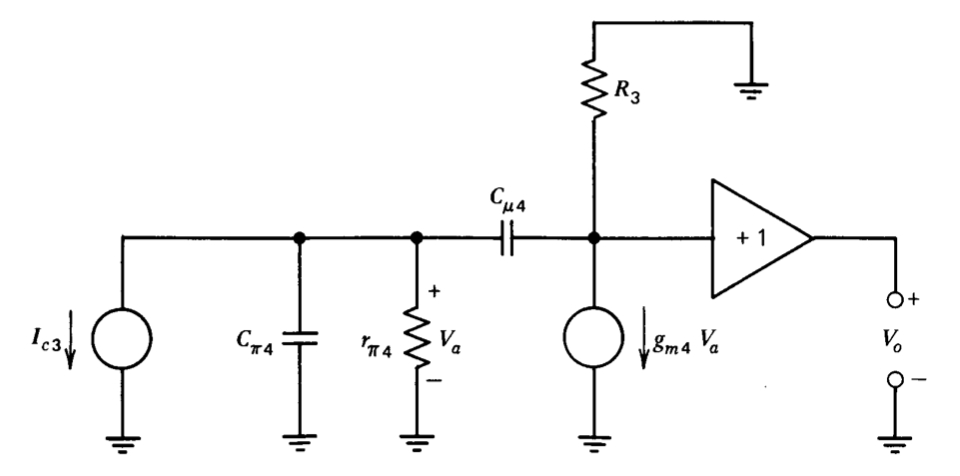
El polo de frecuencia más baja representado en la Figura 8.1 tiene una frecuencia de ruptura de\(1.36 \times 10^4\) radianes por segundo. Este polo es el resultado de la retroalimentación a través de la capacitancia de colector a base de\(Q_4\) (a veces llamado efecto Miller), como lo demuestra el siguiente desarrollo. En la Figura 8.3 se muestra un modelo incremental que puede ser utilizado para evaluar la transimpedancia de la etapa final del emisor común. Esta transimpedancia es un término multiplicativo en la función de transferencia completa del amplificador.
Las ecuaciones de nodo para este circuito son
\[\begin{array} {rcl} {-I_{c3}} & = & {[g_{\pi 4} + (C_{\mu 4} + C_{\pi 4})s] V_a - C_{\mu 4} s V_o} \\ {0} & = & {(g_{m4} - C_{\mu 4})s V_a + (G_3 + C_{\mu 4} s) V_o} \end{array} \nonumber \]
Resolviendo por la transimpedancia demuestra que
\[\dfrac{V_o (s)}{I_{c3} (s)} = \dfrac{\beta R_3 [-(C_{\mu 4}/ g_{m4})s + 1]}{r_{\pi 4} R_3 C_{\mu 4} C_{\pi 4} s^2 + r_{\pi 4} \{[(g_{m4} + g_{\pi 4}) R_3 + 1]C_{\mu 4} + C_{\pi 4} \} s + 1}\label{eq8.2.5} \]
El denominador de Ecuación normalmente\(\ref{eq8.2.5}\) está dominado por el término que incluye el factor\(g_{m4}R_3 C_{\mu 4}\), reflejando la importancia de la retroalimentación a través de\(C_{\mu 4}\). Sustituir los valores de la Tabla 8.1 a la Ecuación\(\ref{eq8.2.5}\) y factorizar los resultados polinomales de nominador en
\[\dfrac{V_o (s)}{I_{c3} (s)} = \dfrac{6 \times 10^6 (-10^{-9} s + 1)}{(10^{-9} s + 1)(6.08 \times 10^{-5} s + 1)}\label{eq8.2.6} \]
Este desarrollo muestra que la etapa de salida tendría un polo dominante con una frecuencia de ruptura\(1.64 \times 10^4\) radianes por segundo en su función de transferencia si los otros componentes del circuito no alteraran la ubicación de este polo. Este valor concuerda con la ubicación del polo dominante para el amplificador completo dentro de aproximadamente 20%.
El álgebra involucrada en obtener este resultado puede ser eludido al reconocer que un unipolar (P. E. Gray y C. L. Searle, Electronic Principles: Physics, Models, and Circuits, Wiley, Nueva York, 1969, pp. 497-503.) (o efecto Miller-effect) aproximación a la entrada ca pacitancia del transistor\(Q_4\) predice un valor
\[C_T = C_{\pi 4} + C_{\mu 4} (1 + g_{m4} R_3)\label{eq8.2.7} \]
La frecuencia de ruptura estimada en este nodo es
\[\omega_h = \dfrac{1}{r_{\pi 4} C_T} = 1.66 \times 10^4 \text{ rad/sec} \nonumber \]
Si bien la ganancia d-c y la ubicación del polo dominante para esta configuración se estiman fácilmente, la ubicación de otras singularidades de función de transferencia se relaciona con los parámetros del amplificador de una manera más compleja.
La característica esencial que se puede obtener de la gráfica de Bode de la Figura 8.2 es que esta función de transferencia está lejos de ser ideal para su uso en muchas conexiones de retroalimentación. El amplificador es irremediablemente inestable si se opera con su entrada no inversora conectada a una tierra incremental y un cable que conecta su salida a su entrada inversora, creando un bucle con\(a\) como se muestra en la gráfica Bode y\(f = 1\). De hecho, si se aplica retroalimentación independiente de la frecuencia alrededor del amplificador, es necesario reducir la magnitud de la transmisión de bucle en un factor de 50 por debajo de la ganancia del propio amplificador para hacerlo estable en un sentido absoluto, y por un factor de 2000 para obtener\(45^{\circ}\) de margen de fase. La atenuación requerida podría obtenerse mediante derivación resistiva de la entrada del amplificador o mediante el uso de una red lag (ver Sección 5.2.4). Cualquiera de estos enfoques compromete severamente la insensibilidad y el rendimiento del ruido en muchas aplicaciones debido a la gran atenuación necesaria para la estabilidad. Normalmente se pueden obtener mejores resultados modificando la dinámica del propio amplificador.
Amplificadores compensadores de tres etapas
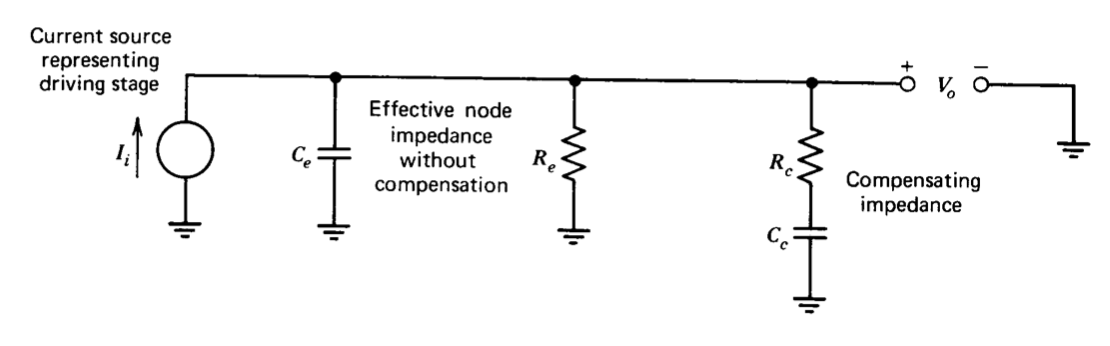
A menudo se utilizan al menos dos métodos para mejorar la dinámica de un amplificador similar a la descrita en la sección anterior. Uno de estos enfoques reconoce que los polos en el amplificador se pueden modelar como ocurriendo debido a los\(R-C\) circuitos ubicados en varios nodos del amplificador. Este tipo de asociación se realizó en la sección anterior para el polo amplificador dominante. La función de transferencia para una etapa de ganancia incluye un término multiplicativo de la forma general\(R_e/(R_eC_e s + 1)\), donde\(R_e\) y\(C_e\) son la resistencia efectiva y capacitancia en un nodo particular (ver Figura 8.4). Si se agrega una\(R-C\) red de compensación en serie a tierra que consiste en una resistencia\(R_c \\ R_e\) y un condensador\(C_c \gg C_e\), la función de transferencia se convierte en
\[\dfrac{V_o (s)}{I_i (s)} \simeq \dfrac{R_e (R_c C_c s + 1)}{(R_e C_c s + 1)(R_c C_e s + 1)} \nonumber \]
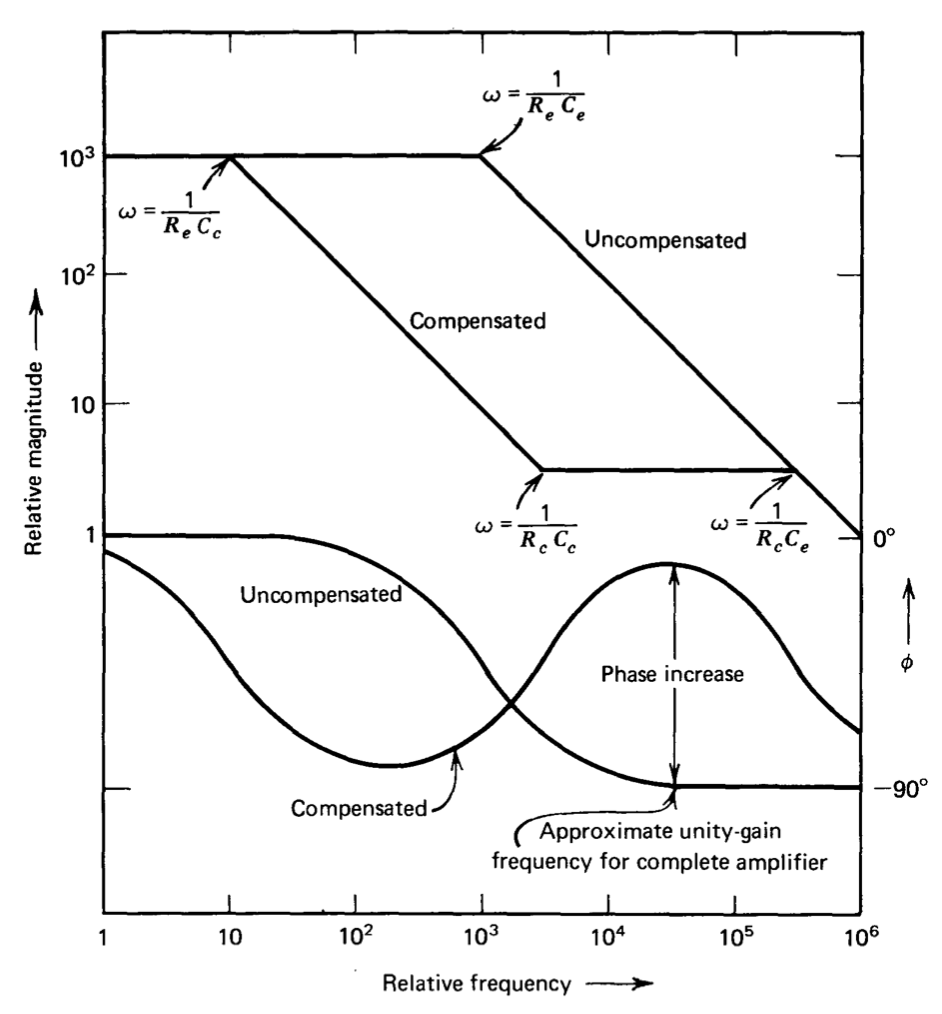
El polo único ha sido sustituido por dos polos y un cero. (Obsérvese que el comportamiento asintótico a frecuencias altas y bajas, que es controlado por\(R_e\) y\(C_c\), no ha sido cambiado.) Los valores de los componentes se eligen de manera que un polo ocurra a una frecuencia mucho menor que el polo original y el otro a una frecuencia por encima de la frecuencia de ganancia unitaria del amplificador completo, como se ilustra en la Figura 8.5. El desplazamiento de fase positivo del cero a menudo puede mejorar el margen de fase del amplificador. Este tipo de compensación se puede ver como una combinación de la función de transferencia no compensada con funciones de transferencia de retraso y plomo ubicadas apropiadamente. Si bien las singularidades deben estar relacionadas para que las funciones de transferencia compensadas y no compensadas sean idénticas a frecuencias muy bajas y muy altas, el segundo polo siempre se puede mover a frecuencias arbitrariamente altas ubicando el primer polo a una frecuencia suficientemente baja.
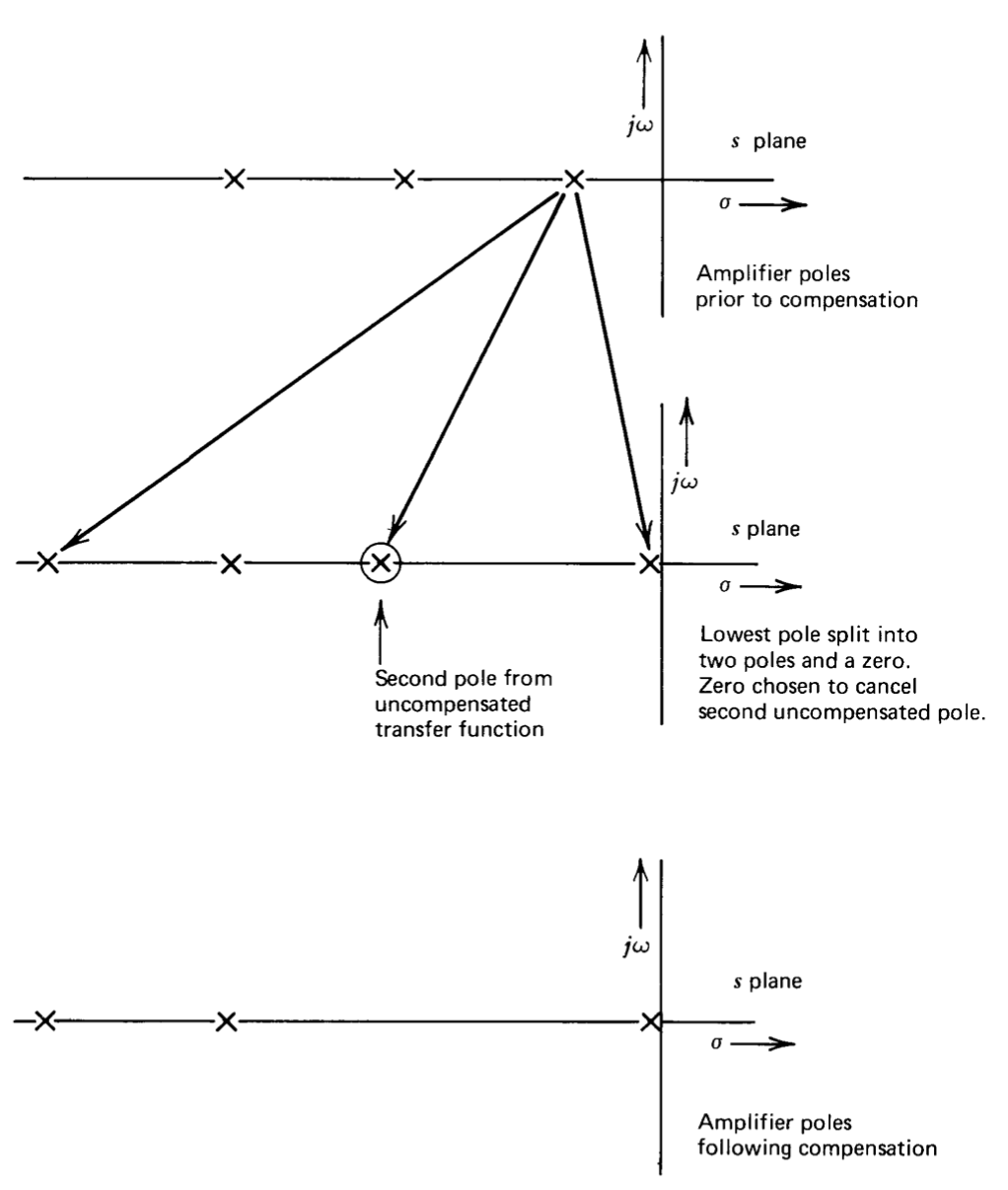
Una forma alternativa de ver este tipo de compensación se muestra en los diagramas del plano s de la Figura 8.6. Se supone que el amplificador de tres etapas tiene tres polos a frecuencias de interés. El polo de menor frecuencia de la tríada se sustituye por dos polos y un cero por medio de una\(R-C\) red de derivación. Una forma posible de elegir ubicaciones de singularidad es usar el cero para cancelar el segundo polo en la función de transferencia original y ubicar el polo de alta frecuencia que resulta de la compensación por encima del polo original de frecuencia más alta. El efecto neto de este tipo de compensación es incrementar la separación de los polos de manera que se pueda lograr una mayor desensitividad para una estabilidad relativa dada.
Existen varias variaciones del esquema de compensación básica. Es posible realizar tipos similares de funciones de transferencia conectando una\(R-C\) red en serie desde el colector a la base de un transistor en lugar de desde su base a un punto de conexión a tierra incremental. El mismo tipo de compensación se puede usar en más de un nodo, y esta compensación múltiple se requiere frecuentemente en amplificadores más complejos.
Si bien este tipo general de compensación es efectivo y se ha aplicado con éxito a varios diseños de amplificadores, es menos que ideal por varias razones. Una de las consideraciones más importantes es que la determinación de los valores de los elementos que dan como resultado una función de transferencia dada requiere cálculos bastante involucrados. Esta dificultad tiende a desalentar al usuario de encontrar los valores óptimos de los elementos de compensación para su uso en aplicaciones distintas a las estándar. Este tipo de compensación también requiere capacitores grandes (típicamente\(1000\ pF\) a\(0.1 \mu F\)) cuando la red se deriva de la base a una tierra incremental. El almacenamiento de energía de un condensador grande puede retrasar la recuperación después de una sobrecarga del amplificador que carga el condensador al nivel de voltaje incorrecto.
Un tipo alternativo de compensación que se puede usar solo o junto con una impedancia de derivación es “alimentar hacia adelante” alrededor de una o más etapas de amplificador como se muestra en la Figura 8.1. Aquí un amplificador de búfer de ganancia de unidad-voltaje-ganancia (no esencial pero incluido en algunos diseños para evitar la carga en el terminal de entrada de inversión) acopla la señal de entrada a la base de condensador\(Q_4\) pasante\(C_f\). Dado que las primeras etapas se omiten a alta frecuencia, la dinámica de alta frecuencia del amplificador operacional debe ser esencialmente la de la etapa de salida. La esperanza es que la etapa de salida tenga solo un polo a frecuencias de interés, y por lo tanto sea estable con cualquier cantidad de retroalimentación independiente de la frecuencia.
Feedforward no está exento de desventajas. La respuesta de frecuencia de un amplificador de alimentación directa es significativamente menor para las señales aplicadas a la entrada no inversora que para las señales aplicadas a su entrada inversora. Por lo tanto, el
amplificador ha reducido severamente el ancho de banda cuando se utiliza en conexiones no inversoras. También hay problemas que se derivan del tipo de funciones de transferencia que resultan de la compensación de feedforward. Por lo general, hay un rolloff de segundo o tercer orden a bajas frecuencias, con la función de transferencia recuperándose a primer orden cerca de la frecuencia de ganancia unitaria. Dado que esta función de transferencia se asemeja a las obtenidas con compensación de retraso, el tiempo de asentamiento puede ser relativamente largo debido a las pequeñas “colas” de amplitud que pueden resultar con la compensación de retraso (ver Sección 5.2.6). También es posible que estos amplificadores se vuelvan condicionalmente estables en ciertas conexiones (Sección 6.3.4). Este tema se investiga en Problema P8.3.
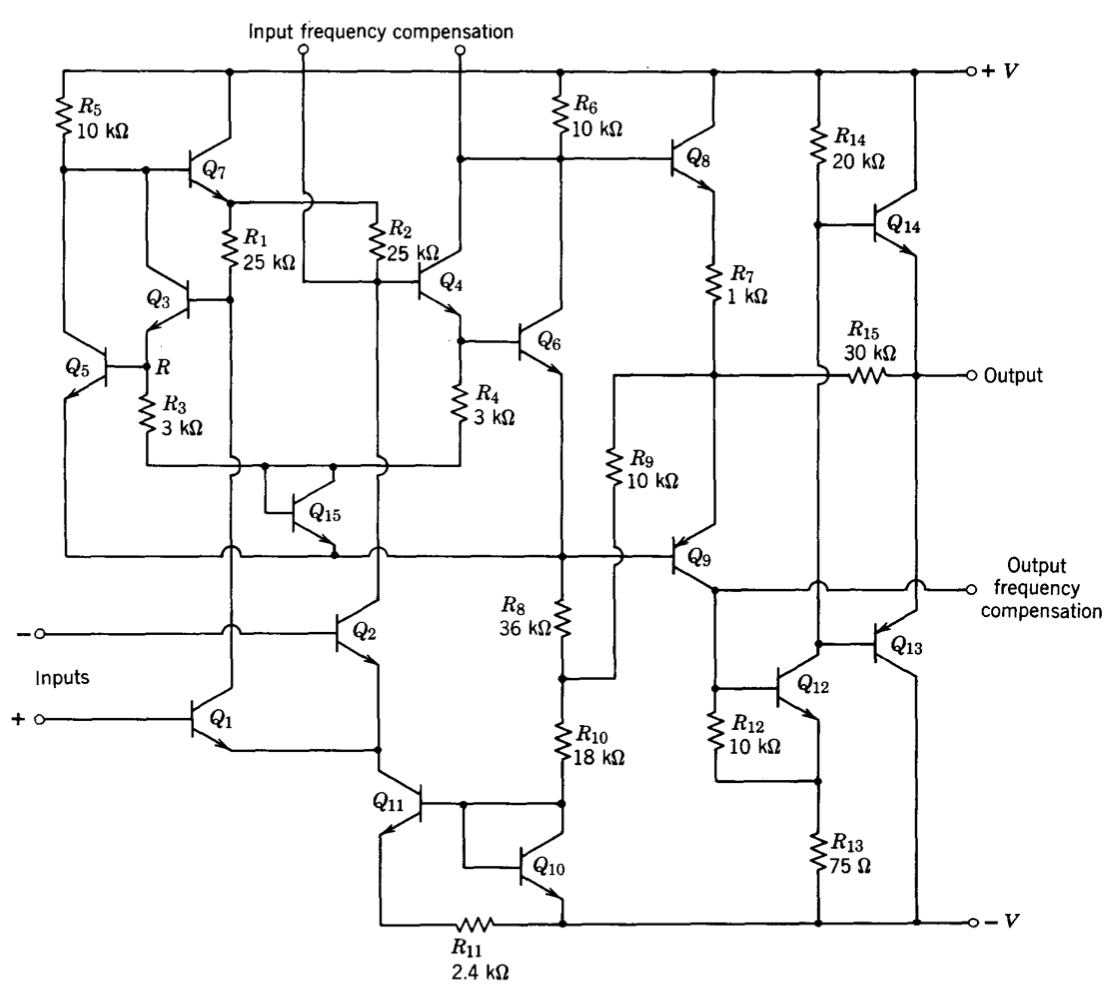
Antes de dejar el tema de los amplificadores de tres etapas, vale la pena señalar la libertad que se ha tomado en la definición de una etapa. Las etapas nunca son tan simples como las que se muestran en la Figura 8.1. La característica esencial que caracteriza una etapa de ganancia de voltaje es que generalmente introduce un polo a frecuencias moderadas. El 709 (Figura 8.7) es un ejemplo de un amplificador de circuito integrado temprano que es un diseño de tres etapas. Si bien no pretendemos investigar en detalle el funcionamiento de este circuito (varios amplificadores modernos y más útiles se describen en el Capítulo 10), la ruta básica de flujo de señal ilustra la naturaleza de tres etapas de este diseño. Transistores\(Q_1\) y\(Q_2\) forman un amplificador diferencial. La amplificación principal de la segunda etapa ocurre a través del par\(Q_4-Q_6\) conectado a Darlington. Transistores\(Q_3\) y\(Q_5\) completar una segunda etapa diferencial con el\(Q_4-Q_6\) par y se incluyen principalmente para reducir la deriva del amplificador. Transistores\(Q_8\) y se\(Q_9\) utilizan para el cambio de nivel, con etapa de emisor común\(Q_{12}\) la etapa final de ganancia de voltaje. Seguidores de emisor\(Q_{13}\) y\(Q_{14}\) función como amplificador de búfer. Se aplica una retroalimentación de bucle menor alrededor de la etapa de salida para linealizar su desempeño y modificar su dinámica vía\(R_{15}\).
La compensación se implementa conectando una\(R-C\) red en serie desde la salida a la entrada de la segunda etapa. También es necesario utilizar retroalimentación capacitiva desde la salida del amplificador a la base de\(Q_{12}\) (esencialmente alrededor de la etapa de salida) para obtener estabilidad aceptable en la mayoría de las aplicaciones.
Diseño de dos etapas
Si bien existen varios diseños de amplificadores operativos con tres (o incluso más) etapas de amplificación de voltaje, es difícil escapar a la conclusión de que uno está luchando contra la naturaleza cuando intenta estabilizar un amplificador con tres
o polos más estrechamente espaciados. La clave para un diseño exitoso de amplificadores operativos es darse cuenta de que la única manera realmente efectiva de eliminar polos en una función de transferencia de amplificador es reducir el número de etapas que producen ganancia de voltaje. Las etapas que proporcionan solamente ganancia de corriente, como los seguidores de emisor, generalmente tienen polos ubicados a frecuencias lo suficientemente altas como para ser ignoradas.
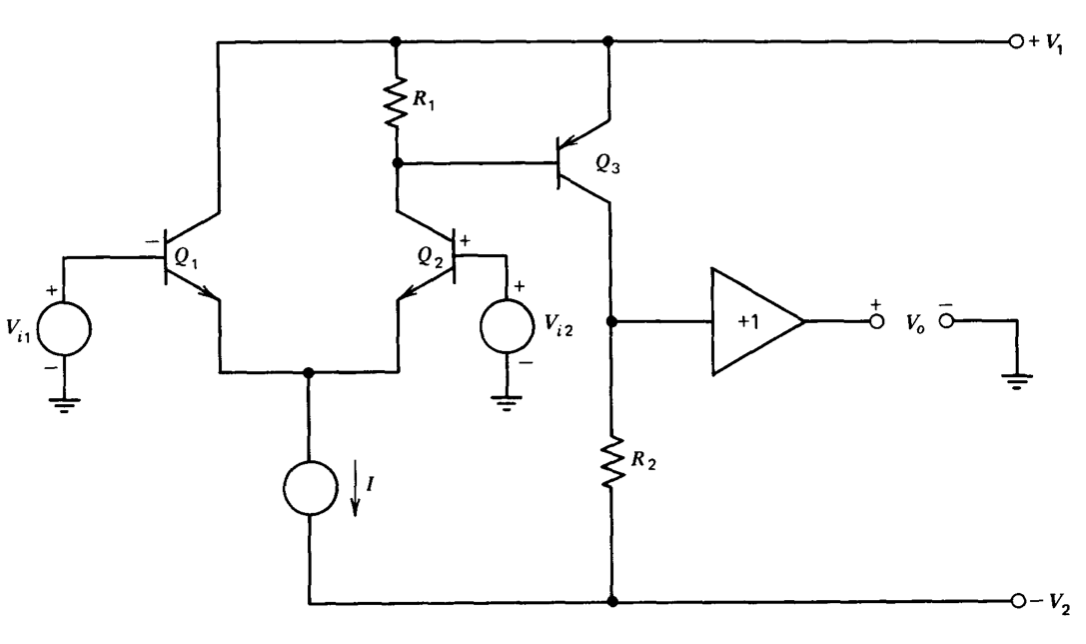
Un amplificador con dos etapas de ganancia de voltaje resulta si se elimina una de las etapas de emisor común de la Figura 8.1, como se muestra en la Figura 8.8. (El gran valor y versatilidad de este amplificador básico y sus muchas variaciones me lo señaló primero el Dr. F. W. Sarles, Jr.) Nuevamente, los transistores\(Q_1\) y\(Q_2\) funcionan como amplificador diferencial. Sin embargo, a diferencia del amplificador anterior, tenga en cuenta que la base del transistor\(Q_1\) es la entrada inversora del amplificador completo, mientras que la salida de primera etapa es el colector de
transistor\(Q_2\). Esta conexión acoplada al emisor asegura una baja pacitancia de ca de entrada (aproximadamente\(C_{\mu 1} + C_{\pi 1}/2\)) en la base\(Q_1\) ya que este dispositivo está funcionando como seguidor de emisor. La baja capacitancia de entrada es una ventaja en muchas aplicaciones ya que la retroalimentación se aplica normalmente desde la salida del amplificador a su terminal de entrada inversora. La capacitancia de entrada en la entrada inversora puede introducir un polo de frecuencia moderada adicional en la transmisión de bucle de la combinación de amplificador-red de retroalimentación con problemas de estabilidad concomitantes. Por lo tanto, la baja capacitancia de entrada aumenta el rango de impedancias de retroalimentación que se pueden usar sin deteriorar la transmisión en bucle.
La función de transferencia para este amplificador calculada usando los valores de los parámetros en la Tabla 8.2 es (Como en el caso del amplificador de tres etapas, el ligero desequilibrio de la etapa de entrada que se produce a altas frecuencias debido a las señales alimentadas directamente a la base de\(Q_3\) vía la capacitancia colector-a-base de \(Q_2\)ha sido ignorada en el análisis que lleva a esta función de transferencia. El error introducido por esta simplificación es insignificante a frecuencias por debajo de la frecuencia de ganancia unitaria del amplificador. Además, la función de transferencia de interés en la mayoría de las aplicaciones de retroalimentación donde la señal de retroalimentación se aplica a la base de\(Q_1\) no incluye el término de alimentación directa asociado con\(C_{\mu 2}\))
\[\dfrac{V_o (s)}{V_{i2} (s) - V_{i1} (s)} = \dfrac{6 \times 10^3}{(3 \times 10^{-4} s + 1)(1.1 \times 10^{-8} s + 1)}\label{eq8.2.10} \]
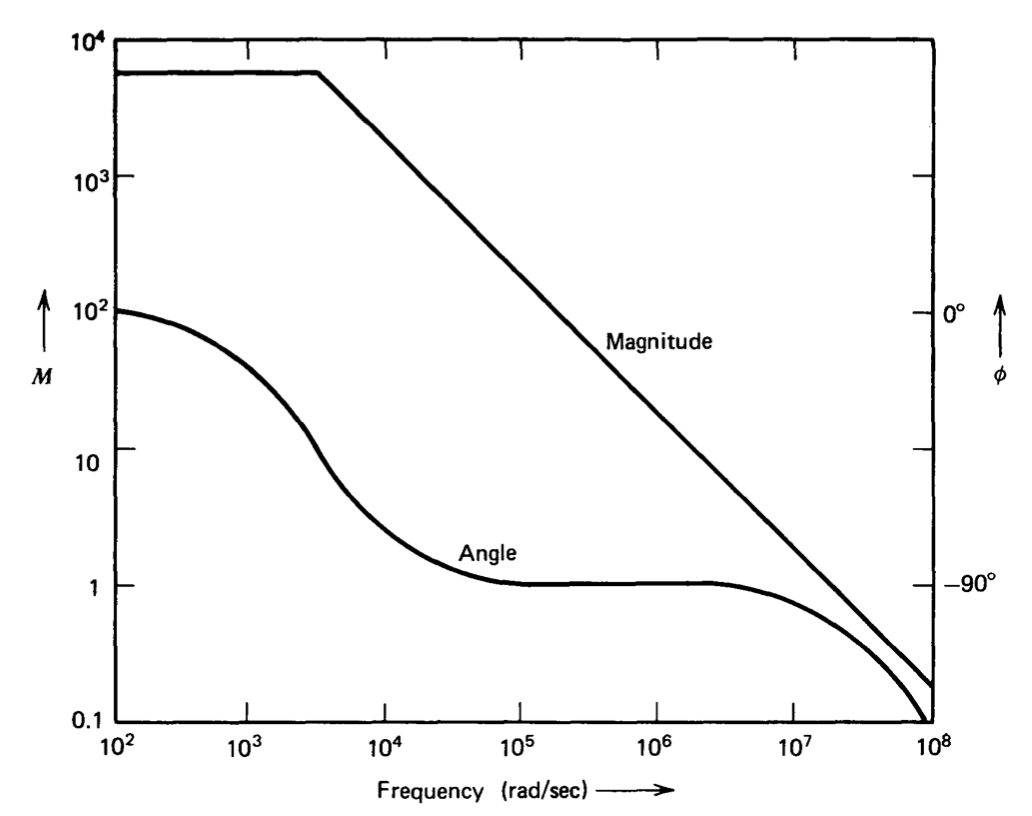
con todas las demás singularidades anteriores\(5 \times 10^8 \text{ sec}^{-1}\). La gráfica Bode correspondiente (Figura 8. 9) muestra que un margen de fase de\(75^{\circ}\) resultados incluso cuando la salida del amplificador se retroalimenta directamente a su entrada inversora. Este tipo de función de transferencia, obtenida sin incluir ningún componente de compensación adicional, contrasta fuertemente con la función de transferencia de amplificador de tres etapas no compensada de la sección anterior.
Es informativo ver por qué la función de transferencia de este amplificador está dominada por un solo polo y por qué el segundo polo está separado del polo dominante por un factor de aproximadamente 30,000. Esta separación, que permite una excelente desensitividad en aplicaciones de retroalimentación manteniendo una buena estabilidad relativa, es una ventaja importante atribuible al diseño de dos etapas. El polo dominante es principalmente el resultado del almacenamiento de energía en la capacitancia colector a base del transistor\(Q_3\). Una\(C_T\) aproximación a la capacitancia de entrada de este transistor es (ver la discusión asociada con la ecuación\(\ref{eq8.2.7}\))
\[C_T = C_{\pi 3} + C_{\mu 3} (1 + g_{m3} R_2) = 6.02 \times 10^{-9}\ F \nonumber \]
La constante de tiempo correspondiente
\[\tau_{B3} = C_T r_{\pi 3} = 3.01 \times 10^{-4} \text{ sec} \nonumber \]
Tabla 8.2 Valores de Parámetros para Ejemplo Usando Amplificador de la Figura 8.8
| Voltajes de alimentación: \(\pm 15\ V\) |
| Corrientes de polarización: \(I_{C1} = I_{C2} = 10 \ \mu A\) \(I_{C3} = 50 \ \mu A\) |
| Transconductancias implícitas por corrientes de sesgo: \(g_{m1} = g_{m2} = 4 \times 10^{-4} \text{ mho}\) \(g_{m3} = 2 \times 10^{-3} \text{ mho}\) |
| Otros parámetros del transistor: \(\beta = 100 \text{ (all transistors)}\) \(r_{\pi 1} = r_{\pi 2} = 250\ k\Omega\) \(r_{\pi 3} = 50\ k \Omega\) \(r_x = 100 \Omega \text{ (all transistors)}\) \(C_{\mu} = C_{\pi} = 10\text{ pF (all transistors)}\) |
| Resistencias: \(R_1 \gg r_{\pi 3}\) \(R_2 = 300 \ k\Omega\) Se supone que el amplificador de búfer tiene impedancia de entrada infinita. |
concuerda con la constante de tiempo dominante en la Ecuación\(\ref{eq8.2.10}\). El punto esencial es que la retroalimentación a través\(C_{\mu 3}\), que en realidad es una forma de compensación de bucle menor (ver Sección 5.3), controla la función de transferencia del amplificador completo a frecuencias entre aproximadamente\(3.3 \times 10^3\) y\(10^8\) radianes por segundo. Como veremos, el mecanismo de retroalimentación de bucle menor que domina el rendimiento del amplificador en este caso se puede utilizar para sacar ventaja para la compensación de amplificadores más complejos que comparten la topología de este circuito.
La mayoría de los amplificadores operativos modernos de alto rendimiento representan extensiones relativamente sencillas del circuito que se muestra en la Figura 8.8, y esta popularidad es una consecuencia directa de la excelente dinámica asociada a la topología. Una modificación importante incluida en la mayoría de los diseños es el uso de una segunda etapa más compleja que el amplificador de emisor común simple que se muestra en la Figura 8.8 para lograr una mayor ganancia de bucle abierto d-c. Existen otras opciones en la forma en que se realiza el circuito de búfer de salida y las modificaciones reductoras de deriva que se pueden incorporar en la primera y segunda etapas.


