11.4: Conexiones lineales representativas
- Page ID
- 84295
El objetivo de muchas conexiones de amplificador operacional es proporcionar una ganancia lineal o función de transferencia entre las señales de entrada y salida del circuito. Esta sección aumenta la colección de aplicaciones lineales que hemos visto en secciones anteriores. Como se mencionó anteriormente, nuestro objetivo al discutir estos
circuitos no es formar un manual de circuitos, sino fomentar la creatividad tan esencial para diseños imaginativos útiles.
Las conexiones presentadas en esta y subsiguientes secciones no incluyen los detalles menores que normalmente dependen fuertemente de los detalles de una aplicación en particular y del amplificador operacional utilizado, y eso oscurecería características más importantes y universales. Por ejemplo, no se intenta equilibrar las resistencias enfrentadas a ambos terminales de entrada, aunque hemos visto que dicho equilibrio reduce los errores relacionados con la entrada del amplificador
corrientes. Tácitamente asumimos que el amplificador con retroalimentación proporciona su ganancia ideal de bucle cerrado a menos que se mencione específicamente lo contrario. De igual manera, se asume la estabilidad. Los métodos utilizados para garantizar este último supuesto son el tema del Capítulo 13.
Amplificadores diferenciales
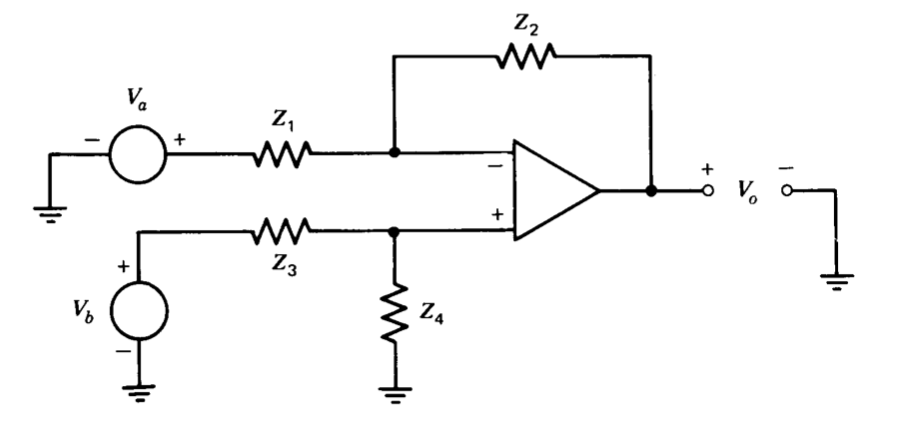
Hemos visto numerosos ejemplos de conexiones de amplificador tanto invertidas como no inversoras. La Figura 11.10 muestra una topología que combina las características de ambas conexiones. La relación ideal entrada-salida se determina fácilmente por superposición. Si\(V_b\) es cero,
\[V_o = -\dfrac{Z_2}{Z_1} V_a \nonumber \]
Si\(V_a\) es cero, el circuito es un amplificador no inversor precedido por un atenuador, y
\[V_o = \left ( \dfrac{Z_4}{Z_3 + Z_4} \right ) \left ( \dfrac{Z_1 + Z_2}{Z_1} \right ) V_b \nonumber \]
La linealidad asegura que en general
\[V_o = \left ( \dfrac{Z_4}{Z_3 + Z_4} \right ) \left ( \dfrac{Z_1 + Z_2}{Z_1} \right ) V_b - \dfrac{Z_2}{Z_1} V_a \nonumber \]
Si se seleccionan valores para que\(Z_4/Z_3 = Z_2/Z_1\).
\[V_o = \dfrac{Z_2}{Z_1} (V_b - V_a) \nonumber \]
Esta conexión se utiliza frecuentemente con cuatro resistencias para formar un amplificador diferencial. El ajuste de cualquiera de las cuatro resistencias se puede utilizar para cero ganancia de modo común. Otras posibilidades implican combinar dos capacitores para\(Z_2\) y\(Z_4\) con dos resistencias para\(Z_1\) y\(Z_3\). Si las constantes de tiempo de las dos combinaciones son iguales, resulta un integrador diferencial o no inversor.
Es importante señalar que la corriente de entrada en el\(V_a\) terminal de la conexión diferencial depende de ambos voltajes de entrada, mientras que la corriente en el\(V_b\) terminal depende únicamente de la tensión\(V_b\). Esta carga asimétrica puede provocar errores en algunas aplicaciones. Se pueden usar dos amplificadores de ganancia de unidad no inversora como búferes para elevar la impedancia de entrada a niveles muy altos si es necesario.
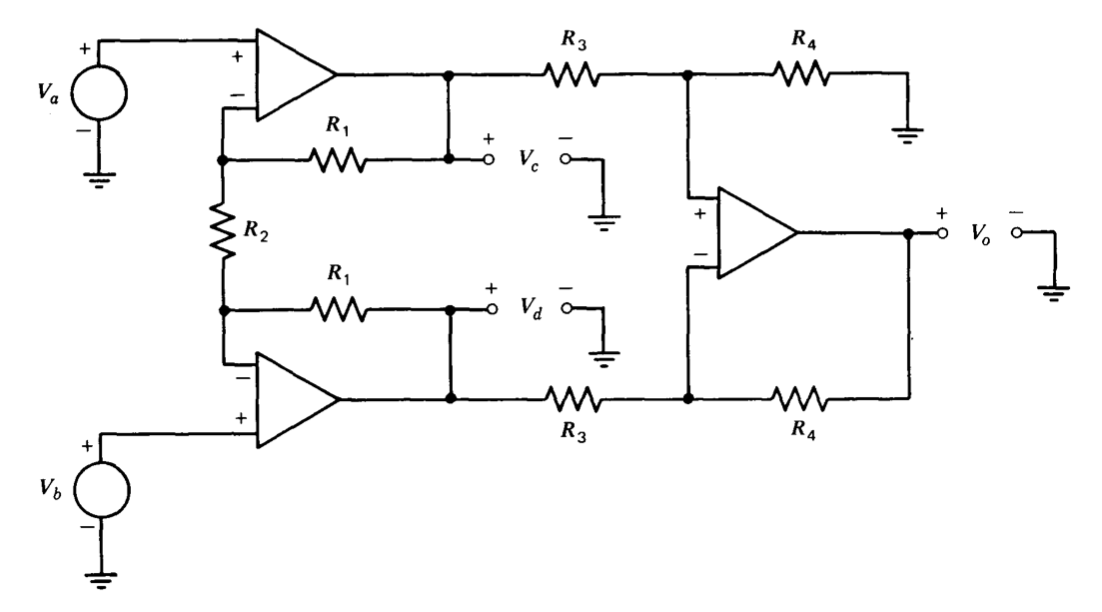
Si el objetivo de diseño es un amplificador diferencial de alta impedancia de entrada con alta relación de rechazo en modo común, se puede utilizar la conexión que se muestra en la Figura 11.11. Considere una señal de entrada de modo común con\(V_a = V_b = V_i\). En este caso los dos amplificadores de la izquierda se combinan para mantener el voltaje a través de\(R_2\) cero. Así, para una entrada de modo común, los voltajes intermedios\(V_c\) y\(V_d\) están relacionados con entradas como
\[V_c = V_d = V_a \ \ \ V_a = V_b \nonumber \]
Alternativamente, considere una señal de entrada diferencial pura con\(V_i/2 = V_a = - V_b\). En este caso, el punto medio de la resistencia\(R_2\) es un punto de conexión a tierra incrementalmente, y cada uno de los amplificadores de la izquierda funciona como un amplificador no inversor con una ganancia de\((2R_1 + R_2)/R_2\). La linealidad asegura que la ganancia diferencial del par izquierdo de amplificadores debe ser independiente del nivel de modo común. Así
\[\dfrac{V_c - V_d}{V_a - V_b} = \dfrac{2R_1 + R_2}{R_2} \nonumber \]
El amplificador derecho tiene una ganancia de cero para el componente de modo común de\(V_c\) y\(V_d\), y una ganancia de\(R_4/R_3\) para el componente diferencial de estas señales intermedias. La combinación de expresiones muestra que\(V_o\) es independiente del componente de modo común de\(V_a\) y\(V_b\), y está relacionado con estas señales como
\[V_o = \left ( \dfrac{R_1 + R_2}{R_2} \right ) \dfrac{R_4}{R_3} (V_a - V_b) \nonumber \]
Además de la alta impedancia de entrada proporcionada por los amplificadores de la izquierda, la ganancia diferencial de este par hace que el rechazo de modo común del amplificador general sea menos sensible a los desajustes de relación de las redes de resistencias de amplificador de salida.
Doble Integrador
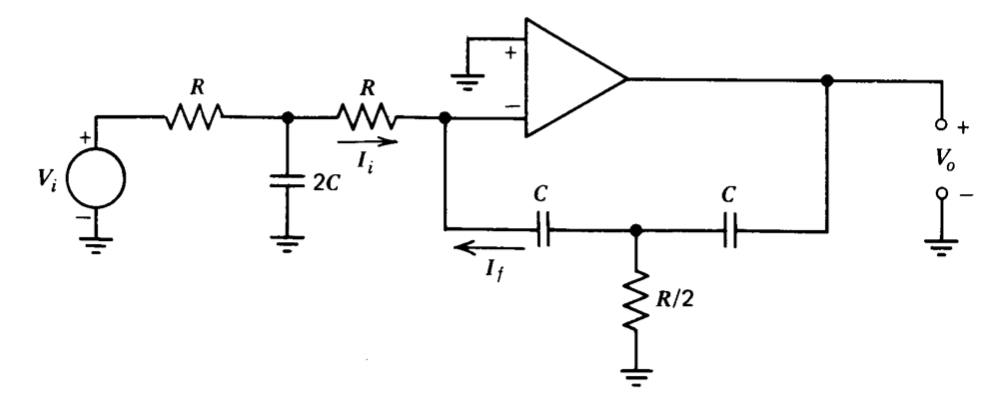
Hemos visto que la integración inversora o no inversora se puede lograr con un amplificador operacional. La Figura 11.12 muestra una conexión que proporciona una integración de segundo orden con un único amplificador operacional. El circuito es analizado por el método virtual-tierra. Suponiendo que la entrada inversora del amplificador está a potencial de tierra
\[I_i (s) = \dfrac{V_i (s)}{2R(RCs + 1)} \label{eq11.4.8} \]
y
\[I_f (s) = \dfrac{RC^2 s^2 V_o (s)}{2(RCs + 1)} \label{eq11.4.9} \]
La corriente de entrada insignificante de las fuerzas del amplificador\(I_f = -I_i\). Combinando y Ecuaciones\(\ref{eq11.4.8}\) y\(\ref{eq11.4.9}\) a través de esta restricción muestra que
\[\dfrac{V_o (s)}{V_i (s)} = -\dfrac{1}{(RCs)^2} \nonumber \]
Fuentes de corriente
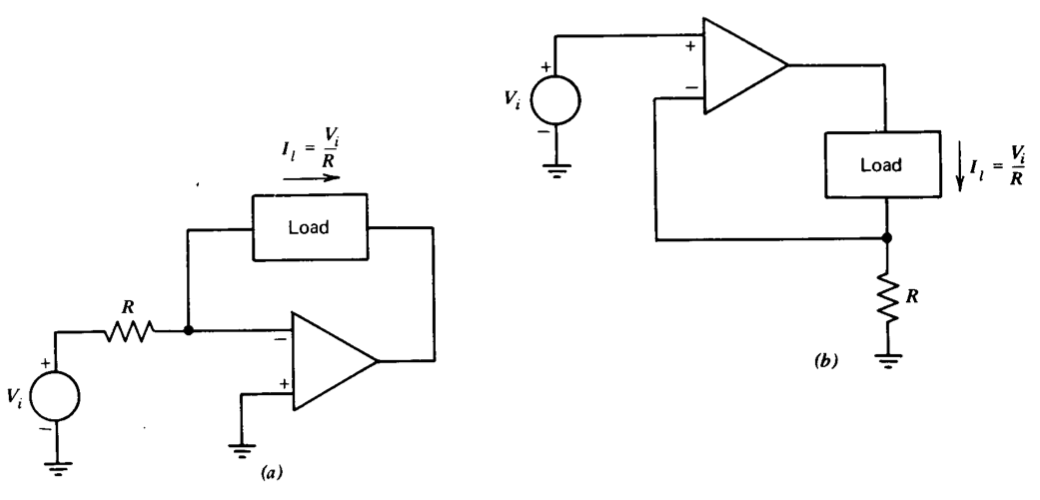
El amplificador operacional se puede utilizar como fuente de corriente de varias maneras diferentes. La Figura 11.13 muestra dos configuraciones simples. En parte\(a\) de esta figura, la carga sirve como impedancia de realimentación de un amplificador operacional conectado de inversión. El método de tierra virtual muestra que la corriente a través de la carga debe ser igual a la corriente a través de la resistencia\(R\). En parte\(b\), el amplificador operacional obliga a que el voltaje\(R\) a través sea igual al voltaje de entrada. Dado que la corriente requerida en el terminal de entrada de inversión del amplificador es insignificante, la corriente de carga es igual a la corriente a través de la resistencia\(R\).
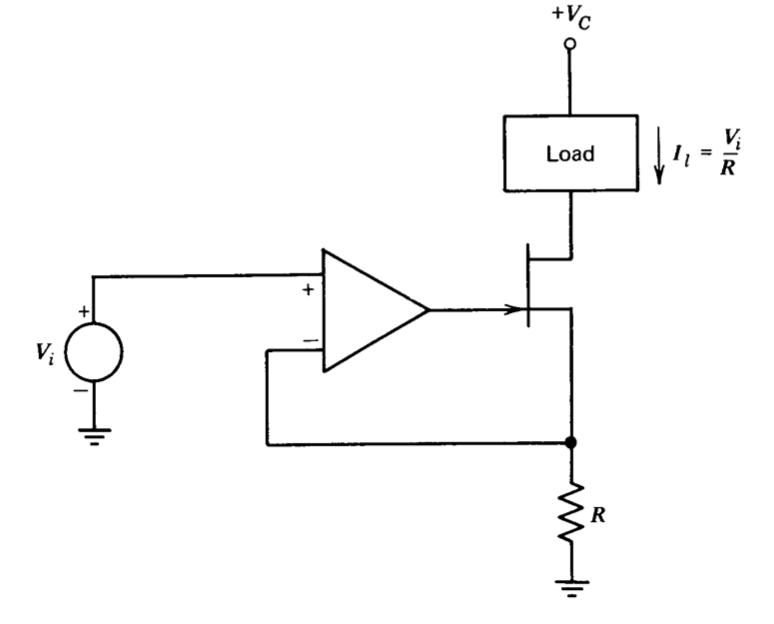
Ambas conexiones corriente-fuente descritas anteriormente requieren que la carga sea flotante. La configuración mostrada en la Figura 11.14 relaja este requisito. Aquí el amplificador operacional limita la corriente de fuente de un transistor de efecto de campo. Siempre que los niveles operativos sean tales que la puerta FET sea polarizada de forma inversa, las corrientes de fuente y drenaje de este dispositivo son idénticas. Así, el amplificador operacional controla la corriente de carga indirectamente.
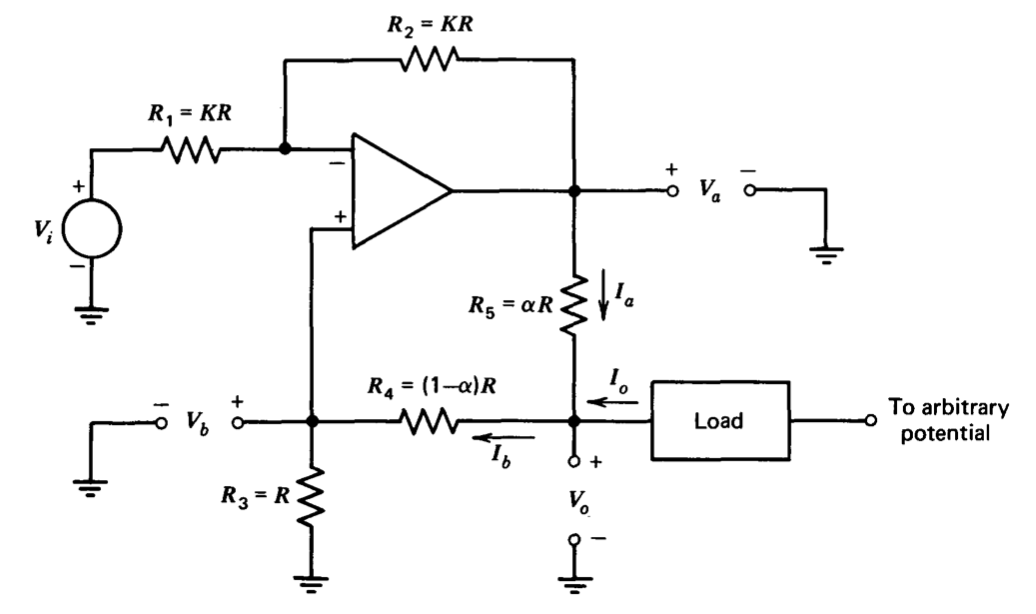
Los niveles operativos relativos del circuito que se muestran en la Figura 11.14 deben restringirse para mantener el FET en su región de funcionamiento directo con su puerta polarizada inversa para un rendimiento satisfactorio. La fuente de corriente Howland mostrada en la Figura 11.15 permite una mayor libertad en la elección de los niveles de operación.
El análisis de este circuito se simplifica al señalar que el amplificador operacional se\(V_a\) relaciona con\(V_i\) y\(V_b\) como
\[V_a = -V_i + 2V_b \label{eq11.4.11} \]
La topología del circuito implica las relaciones
\[I_o = I_b - I_a \nonumber \]
\[I_a = \dfrac{V_a - V_o}{\alpha R} \nonumber \]
\[I_b = \dfrac{V_o - V_b}{(1 - \alpha )R} \nonumber \]
y
\[V_b = \dfrac{V_o}{2 - \alpha} \label{eq11.4.15} \]
Las relaciones de transferencia de interés para este circuito son la transconductancia de voltaje de entrada a cortocircuito de corriente de salida\(I_o/ V_i\) y la conductancia de salida del circuito\(I_o/V_o\). Resolver ecuaciones\(\ref{eq11.4.11}\) a través\(\ref{eq11.4.15}\) de estas conductancias muestra que
\[\dfrac{I_o}{V_i}|_{V_o = 0} = \dfrac{1}{\alpha R} \nonumber \]
y
\[\dfrac{I_o}{V_o}|_{V_i = 0} = 0 \nonumber \]
Dado que la corriente de salida es independiente del voltaje de salida, podemos modelar el circuito como una fuente de corriente con una magnitud dependiente del voltaje de entrada. Si bien la resistencia de salida de esta fuente de corriente es independiente de la cantidad\(\alpha\), este parámetro sí afecta al factor de escala. Los valores más pequeños\(\alpha R\) también permiten una mayor corriente de salida máxima para un nivel de saturación de voltaje de salida dado del amplificador operacional. Existe una compensación involucrada en la selección de\(\alpha\), sin embargo, ya que valores más pequeños para este parámetro dan como resultado mayores corrientes de error para una tensión de compensación dada referida a la entrada del amplificador (ver Problema P11.11).
Hay más libertad en la selección de las relaciones relativas de resistencia, ya que una extensión del análisis anterior muestra que la resistencia de salida es infinita proporcionada\(R_2/R_1 =(R_4+R_5)/R_3\).
Es interesante señalar que el éxito de esta fuente actual en realidad depende de la retroalimentación positiva. Considera un voltaje\(V_o\) aplicado al terminal de salida del circuito. La corriente que fluye a través de la resistencia\(R_4\) se equilibra exactamente por la corriente suministrada desde la salida del amplificador operacional a través de la resistencia\(R_5\). El voltaje en la salida del amplificador operacional es la misma polaridad\(V_o\) y tiene una magnitud mayor que esta variable.
Debemos señalar además que la resistencia\(R_3\) no tiene que estar conectada a tierra, sino que también puede funcionar como un terminal de entrada. En esta configuración la corriente de salida es proporcional a la diferencia entre los voltajes aplicados a las dos entradas.
Circuitos que proporcionan una impedancia de punto de conducción controlada
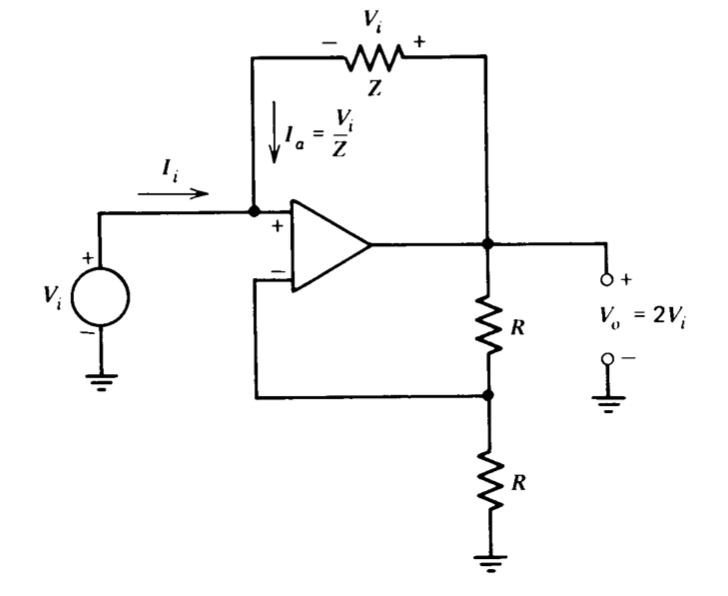
Hemos visto ejemplos de circuitos diseñados para producir impedancias de entrada o salida muy altas o muy bajas. También es posible utilizar amplificadores operativos para producir impedancias de salida o punto de conducción controladas con precisión. Considera el circuito que se muestra en la Figura 11.16. El amplificador operacional está configurado para proporcionar una ganancia no inversora de dos. Como resultado de esta ganancia, la impedancia conectada entre la salida del amplificador y su entrada no inversora tiene un voltaje\(V_i\) a través de ella con una polaridad como se muestra en la Figura 11.16. Dado que se requiere corriente insignificante en la entrada inversora del amplificador, la corriente de entrada requerida de la fuente es
\[I_i = -I_a = -\dfrac{V_i}{Z} \label{eq11.4.18} \]
Resolviendo la ecuación\(\ref{eq11.4.18}\) para la impedancia de entrada de los rendimientos del circuito
\[\dfrac{V_i}{I_i} = -Z \label{eq11.4.19} \]
\(\ref{eq11.4.19}\)La ecuación muestra que este circuito tiene suficiente retroalimentación positiva para producir impedancias de entrada negativas.
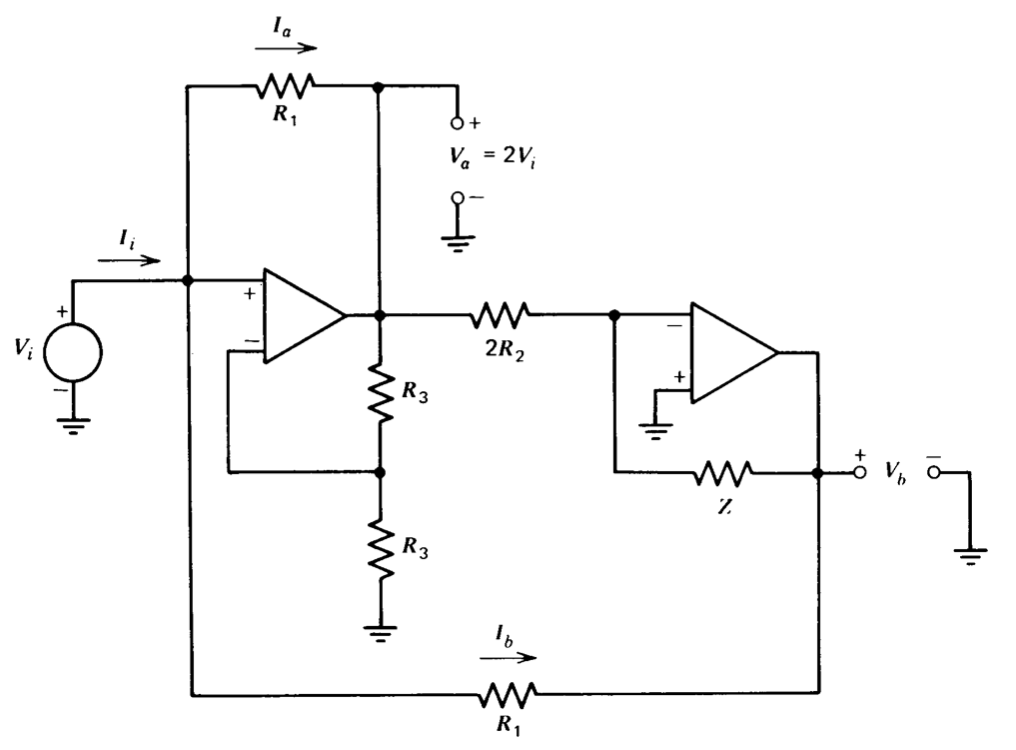
El girador mostrado en la Figura 11.17 es otro ejemplo de un circuito que proporciona una impedancia de punto de conducción controlada. Las relaciones de circuito incluyen
\[I_i = I_a + I_b \label{eq11.4.20} \]
\[I_a = \dfrac{V_i - V_a}{R_1} = \dfrac{-V_i}{R_1} \nonumber \]
\[I_b = \dfrac{V_i - V_b}{R_1} \nonumber \]
\[V_b = -\dfrac{V_i Z}{R_2} \label{eq11.4.23} \]
La combinación\(\ref{eq11.4.20}\) de ecuaciones\(\ref{eq11.4.23}\) y la resolución de la impedancia del punto de conducción muestra que
\[\dfrac{V_i}{I_i} = \dfrac{R_1 R_2}{Z} \nonumber \]
Vemos que el girador proporciona una impedancia de punto de conducción que está relacionada recíprocamente con otra impedancia de circuito. Las aplicaciones incluyen la síntesis de elementos que funcionan como inductores usando solo capacitores, resistencias y amplificadores operativos. Por ejemplo, si elegimos impedancia\(Z\) para ser un\(1-\mu F\) condensador y\(R_1 = R_2 = 1\ k\Omega\), la impedancia del punto de conducción del circuito mostrado en la Figura 11.17 es\(s\), equivalente a la de un inductor de 1-henry.


